💞💞 前言
hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:大耳朵土土垚的博客
💥 所属专栏:数据结构学习笔记 、排序算法合集
💥对于数据结构顺序表、链表、堆以及排序有疑问的都可以在上面数据结构专栏和排序合集专栏进行学习哦~ 有问题可以写在评论区或者私信我哦~
前面我们学习过七种排序——直接插入排序、希尔排序、直接选择排序、堆排序、冒泡排序、快速排序和归并排序,它们都是通过两数之间进行比较来排序的,今天我们就来学习非比较排序中的计数排序🥳🥳🥳
1.计数排序
基本思想:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
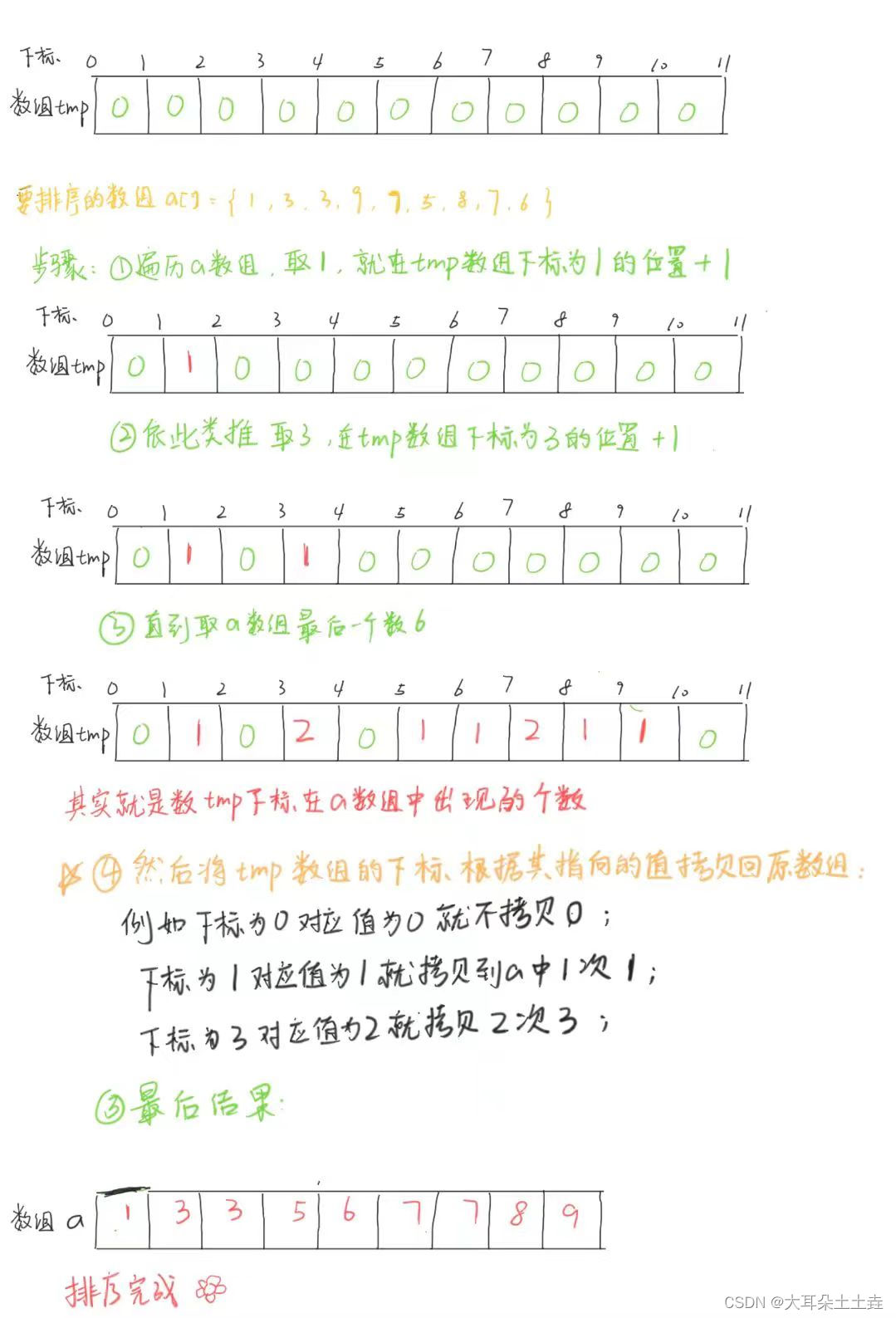
我们这里利用malloc开辟一个数组来统计相同元素出现的次数,用该数字下标表示相同元素,下标对应的值来统计次数
图示如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
void CountSort(int* a, int n)
{//开辟数组int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}//将tmp数组的值初始化为0for (int i = 0; i < n; i++){tmp[i] = 0;}//遍历afor (int i = 0; i < n; i++){//tmp下标对应值要++tmp[a[i]]++;}//拷贝回元素组aint j = 0;//记录a下标for (int i = 0; i < n; i++){while (tmp[i]--){a[j++] = i;}}free(tmp);
}
int main()
{int a[] = { 1,3,3,9,7,5,8,7,6 };printf("排序前:");for (int i = 0; i < 9; i++){printf("%d ", a[i]);}printf("\n");CountSort(a, 9);printf("排序后:");for (int i = 0; i < 9; i++){printf("%d ", a[i]);}printf("\n");return 0;
}
结果如下:
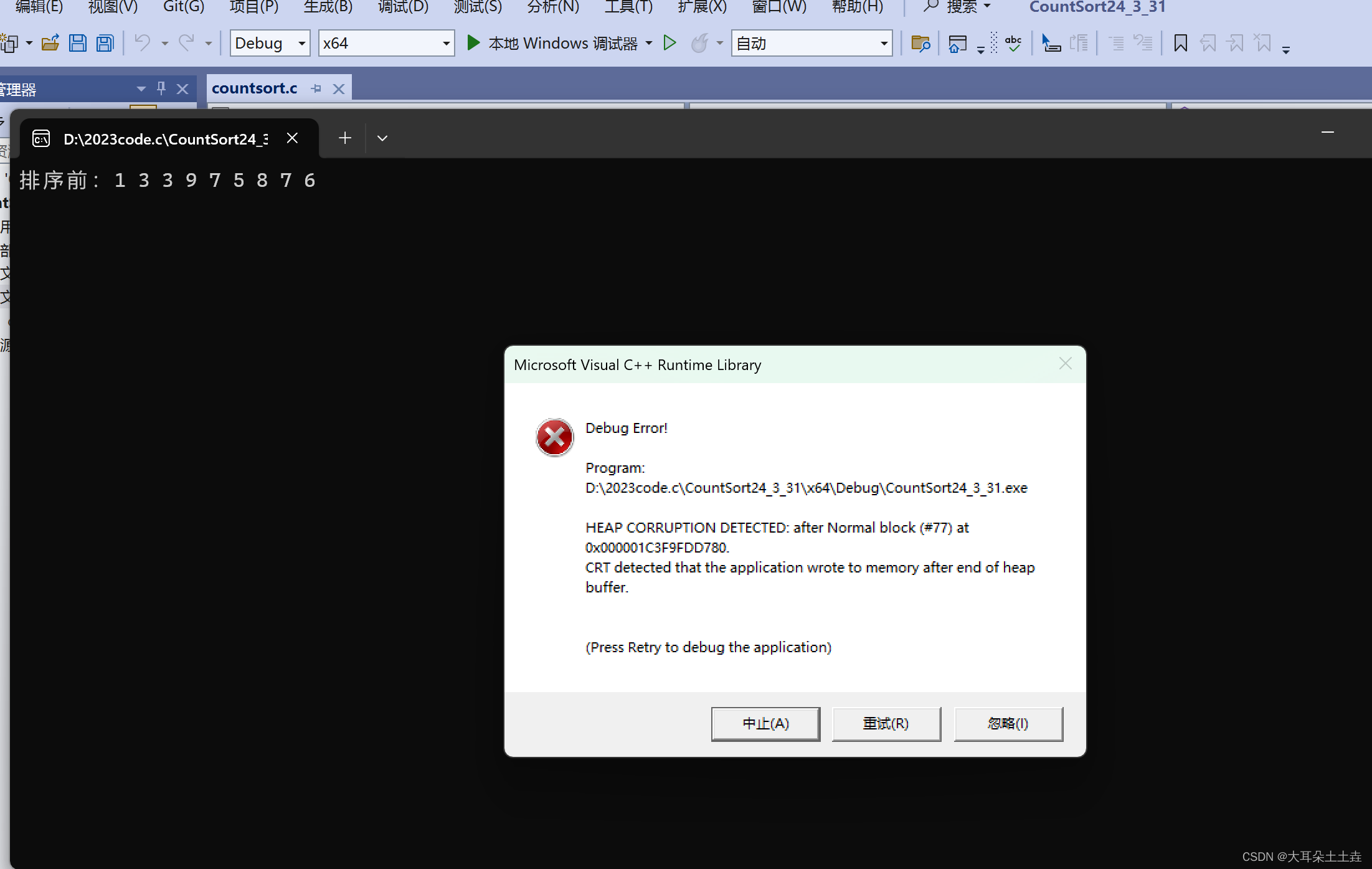
🥲我们仔细观察发现我们开辟tmp数组的大小是n:
int* tmp = (int*)malloc(sizeof(int) * n);
而数组a里面有九个数,也就是tmp大小为9,下标最大也就是8,那么当a中出现比8大的数9时应该怎么计数呢?就不可以计数了,所以出错了;
✨✨那么我们应该开辟多大的数组呢?应该根据什么来开辟才可以呢?
根据a数组最大最小值之差来开辟好像可以,a数组之间的范围就可以作为判断标准;但是这次我们得考虑得全面一点,如果a数组是这样得:a[] = {45,43,36,50,49,44,47}这些呢?那我们岂不是要开辟50个int大小的数组才可以有这么大的下标,如果是考虑范围就是最大50-最小36 = 14,更不可以了;
✨✨解决办法:
利用相对值,还是开辟最大-最小的范围大小数组,然后最后拷贝数据的时候让下标+最小的数即可:
代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
void CountSort(int* a, int n)
{//求a数组最大最小差的范围int small = a[0];int big = a[0];for (int i = 1; i < n; i++){//求最大值if (a[i] > big){big = a[i];}//求最小值if (a[i] < small){small = a[i];}}//范围int gap = big - small;//比如0~4,差就是4,但是对应开辟的大小得是5,0~4有五个数//开辟数组int* tmp = (int*)malloc(sizeof(int) * (gap+1));if (tmp == NULL){perror("malloc fail");return;}//将tmp数组的值初始化为0for (int i = 0; i < gap+1; i++){tmp[i] = 0;}//遍历afor (int i = 0; i < n; i++){//tmp下标(a数组对应值-small)对应值要++tmp[a[i]-small]++;}//拷贝回元素组a,记得+samllint j = 0;//记录a下标for (int i = 0; i < gap+1; i++){while (tmp[i]--){a[j++] = i + small;}}free(tmp);
}
int main()
{int a[] = { 1,3,3,9,7,5,8,7,6 };printf("排序前:");for (int i = 0; i < 9; i++){printf("%d ", a[i]);}printf("\n");CountSort(a, 9);printf("排序后:");for (int i = 0; i < 9; i++){printf("%d ", a[i]);}printf("\n");return 0;
}
结果如下:
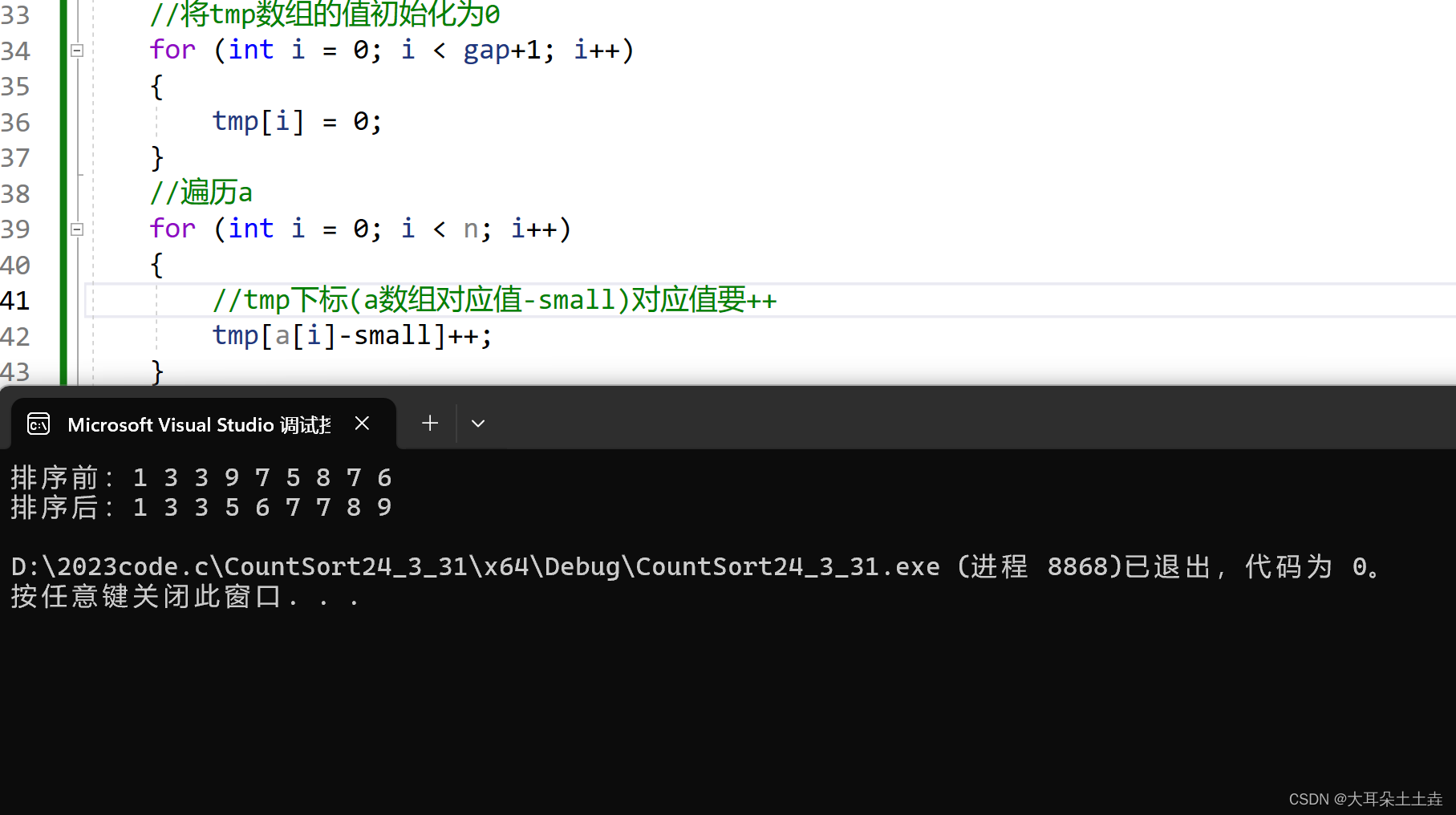
当int a[] = {45,43,36,50,49,44,47}时结果如下:
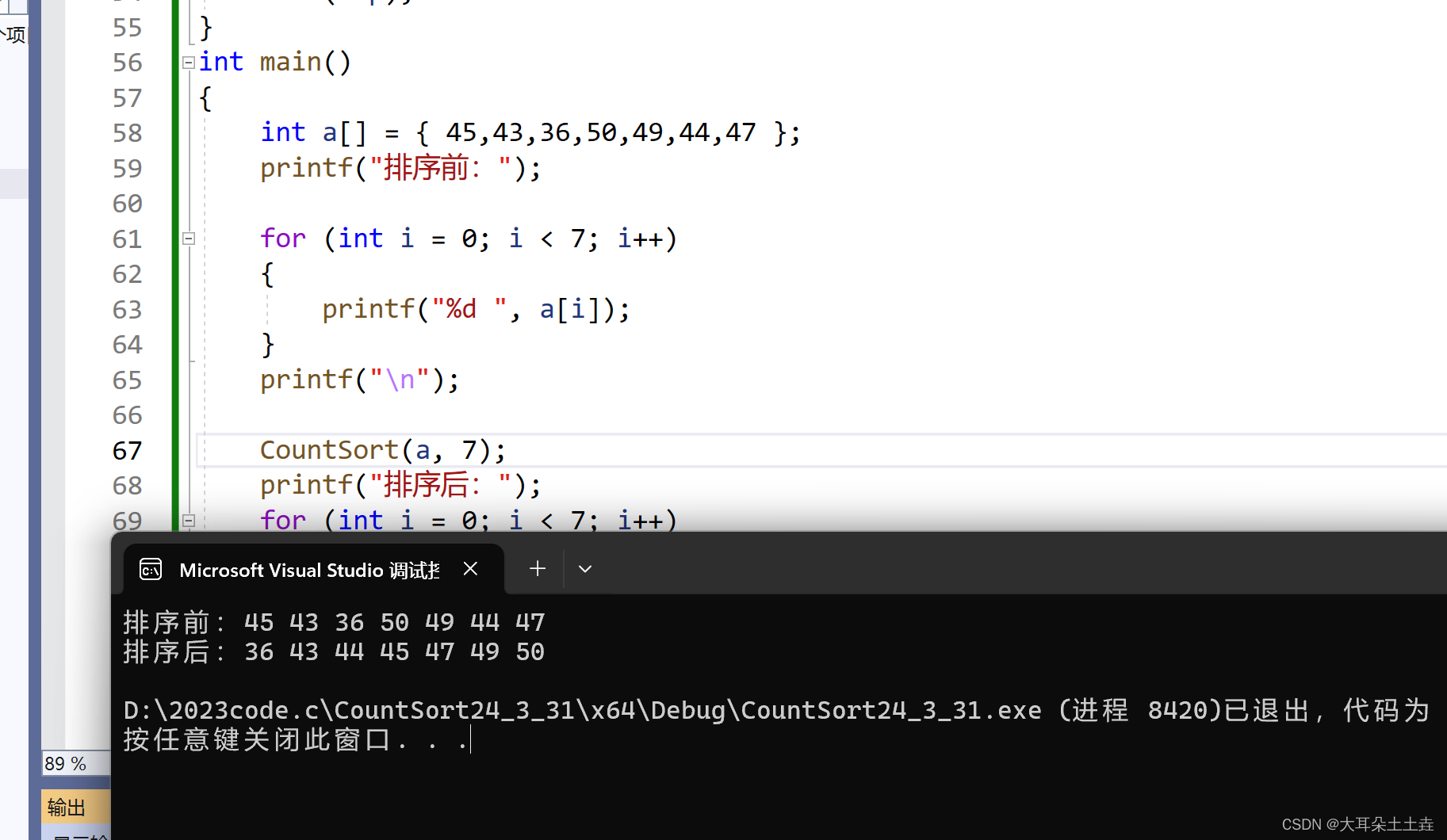
可以发现,计数排序成功啦~🥳🥳🥳
2.计数排序复杂度分析
2.1空间复杂度
我们根据上述代码实现可以知道计数排序开辟了大小为gap的数组,而gap对应的是最大与最小值的差也就是范围,所以其空间复杂度应该为O(gap);
2.2时间复杂度
时间复杂度:
①求数组a最大最小值时遍历了一遍数组a,次数为n;
②初始化tmp数组为0时遍历了数组tmp,次数为gap;
③统计下标出现次数时遍历数组a,次数为n;
④拷贝回原数组时,遍历了数组tmp,次数为gap;
所以其时间复杂度应该是n+gap+n+gap,简化为O(n+gap);
3.计数排序缺陷分析
前面我们学习的七大排序,时间复杂度最好也要O(n*logn);
而计数排序时间复杂度却可以达到O(n);
俗话说金无足赤,人无完人;计数排序达到这么好的时间复杂度其对应的缺陷也是非常明显的:
💥 缺陷1:依赖数据范围,适用于范围集中的数组
💥 缺陷2:只能用于整形(因为使用数组下标来统计)
所以计数排序使用的条件是非常苛刻的
4.结语
计数排序的关键在于理解并运用它的思想, 以上就是计数排序的介绍与实现啦~,完结撒花 ~🥳🥳🎉🎉🎉
















)
(第三期))


