1.1 缓存穿透
原因:当我们查询一个数据的时候,缓存中没有,就会去查询我们的关系型数据库,而且查询不到的数据是不会放到我们的缓存中,就会导致我们每次的请求都会来到我们的关系型数据库中,从而导致关系型数据库宕机。
解决:
(1)缓存空数据:查询返回的数据为空,仍把这个空结果进行缓存
优点:简单
缺点:消耗内存,可能发生缓存与数据库不一致(万一,后面的时候,我们在关系型数据库存储了这个数据呢)
(2)布隆过滤器:当我们在查询redis数据库之前,我们要先查询布隆过滤器,若不存在,直接pass,布隆过滤中存在,则查redis,但前提是在做缓存预热的时候,要初始化好布隆过滤器。
优点:它是二进制数组组成的内存占用少,且基于我们数组的特性,查询也是非常快的
缺点:实现复杂,存在误判。

简介 布隆过滤器
布隆过滤器:快速判断一个元素是否存在于一个集合中。它通过使用bit数组和多个哈希函数来实现
数据经过我们一系列的hash函数运算算出来对应的hash值,然后映射到我们的二进制的数组下标,然后标记,把对应的0变成1。

优点:它是二进制数组组成的内存占用少,且安全性好,且基于我们数组的特性,查询也是非常快的。
缺点:它是一个概率性的数据结构,存在一定的误判率,即可能判断一个元素存在于集合中,但实际上并不存在。因为他是应该hash函数运算的,可能两个值的hash函数值一样。其次,无法删除已插入的元素,因为删除元素会影响其他元素的判断结果。最后我们要权衡一下误判率,数组越大,hash函数越大,误判率越小。同时我们的内存占用空间也会变大很多,查询起来,也比较费时间。我们项目中一般是5%以内的误判率一般的项目也能接受,不至于高并发下压倒数据库。
RedissonClient中自带了布隆过滤器,我们可以设置长度和误差率。
-
若数据库中存在数据,那么布隆过滤器就会在该数据请求过后标记数据的存在,从而避免大量不存在数据请求数据库
1.2 缓存击穿
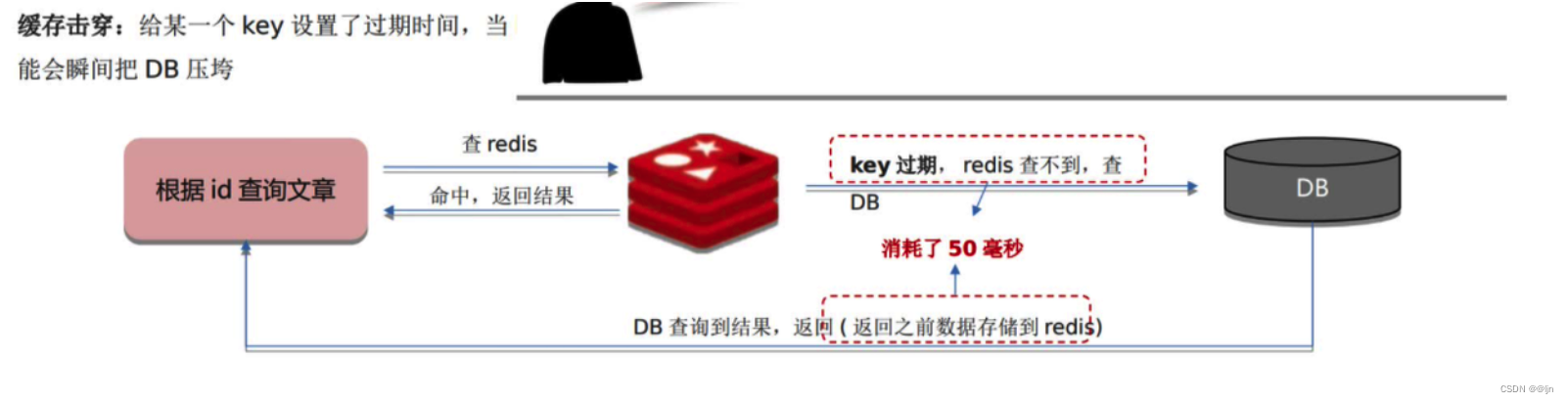
原因:当某一个key设置的时间过期了,恰好key过期这个时间点有大量的并发请求过来,这些并发请求可能瞬间把DB压垮。(虽然我们数据库查询到的数据,会存储redis,但:存储需要一定时间)
解决方案:
- 对于热点数据我们可以先不设置过期时间,或在访问数据的时候,对数据过期时间进行续期。
- 使用分布式锁,当缓存失效的时候,不是先从数据库中加载,而是先获取分布式锁,获取分布式锁的线程从数据库查询数据后写回到缓存中,后续没有获取锁的线程只需要等待和重试即可。这样就能避免大量请求压到数据库,虽然牺牲了一定的性能,但确保了数据库的一个稳定性。
1.3 缓存雪崩
缓存雪崩:同一时间段大量的缓存key同时失效或者Redis服务宕机,导致大量的请求到达数据库,带来压力。
与缓存穿透区别:这是大量的key 穿透是一个key
解决方案:
将缓存失效时间分散开,例如:在原有的时间上增加一个随机值,这样缓存的重复率就会降低很多。
拓展:
(1)给业务增加多级缓存:Guava或者Caffenie
(2)给缓存业务增加降级限流策略:ngxin 或 Spring cloud gateway
Redis宕机这个:可以用Redis集群提高服务的可用性(哨兵模式,集群模式)




)

)


——双O(n)复杂度)



![Kafka配置与部署CentOS7[]](http://pic.xiahunao.cn/Kafka配置与部署CentOS7[])

学习(七):K8S之系统核心组件)


)
)