具有非常详尽的数学推导过程

概述

定位

比较	传统机器学习	深度学习
特征	人工定义	机器生成
模型	决策树、SVM、贝叶斯等（具有不同数学原理）	神经网络

概率论

联合概率$P(X,Y)=P(X|Y)P(Y)=P(Y|X)P(X)$
=>贝叶斯法则$P(X|Y)=\frac{P(Y|X)P(X)}{P(Y)}$
均匀分布$p(x)=\frac{1}{U-L}$
正态分布（概率密度函数）$p(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})$

向量

范数$||a|{|}_2=\sqrt{{\sum }_{i=1}^m{a}_i^2}\ge 0$ for all a

矩阵

如果可能，此处应当补充关于矩阵的更多知识（超出线性代数课程），如pca主成分分析。详见线性代数、矩阵论。
矩阵特征值和特征向量 $Ax=\lambda x$
对称性
正定型（特征值均为非负数）
正交矩阵

函数求导

详见微积分

标量、向量、矩阵间的求导运算

标量对标量求导=1

$x=\left(\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_m\end{array}\right),\frac{\partial y}{\partial x}=\left(\begin{array}{c}\frac{\partial y}{\partial x_1},\frac{\partial y}{\partial x_2},...,\frac{\partial y}{\partial x_m}\end{array}\right)$称为分母布局

$y=\left(\begin{array}{c}{y}_1\\ y_2\\ ...\\ y_m\end{array}\right),\frac{\partial y}{\partial x}=\left(\begin{array}{c}\frac{\partial y_1}{\partial x}\\ \frac{\partial y_2}{\partial x}\\ ...\\ \frac{\partial y_m}{\partial x}\end{array}\right)$称为分子布局
此处有些不清楚，详见矩阵求导的本质与分子布局、分母布局的本质（矩阵求导——本质篇）

机器学习基本流程

分为：有监督学习（占大头）、无监督学习、半监督学习、强化学习
k折交叉验证，用于评估算法的准确度：

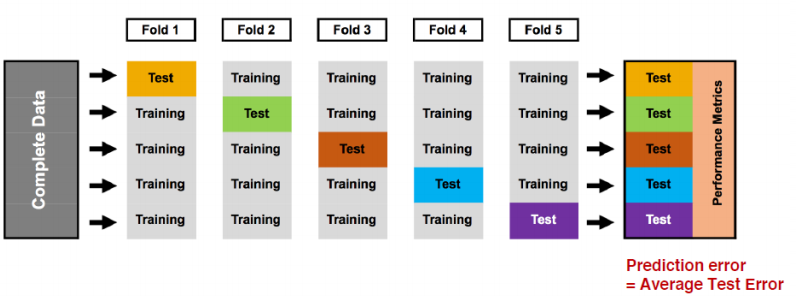
欠拟合和过拟合：

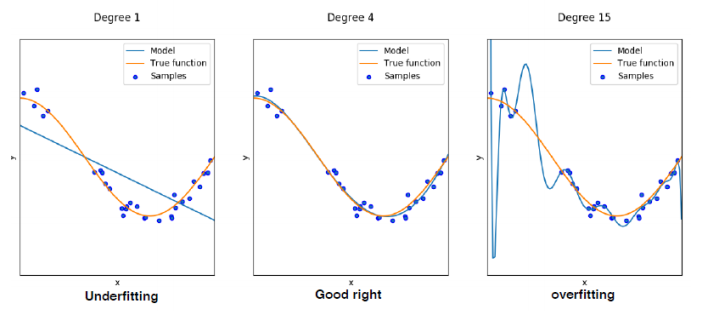
克服过拟合的方法：权重衰减，平方正则化作为硬/软约束

深度学习框架

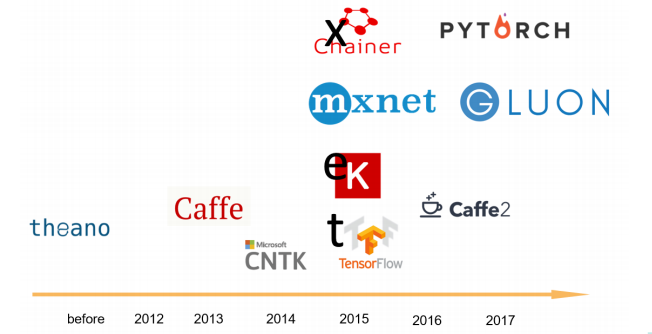
学生多用pytorch，企业多用tensorflow，还有百度的paddlepaddle，此外，c++的框架是caffe

DNN 前向（深度）神经网络（感知机）

感知机

给予输入x，权重w，偏置(bias)b，感知机输出：
$o=\sigma (w\cdot x+b)$，其中wx是向量点积，$\sigma (x)$是激活函数。
最早的感知器非常简单，由Rosenblatt在1957年提出，只有两层神经元，只能对线性数据进行分辨。这还曾经导致人们对神经网络的计算能力产生了严重的怀疑，很大程度上阻碍了神经网络研究的发展。

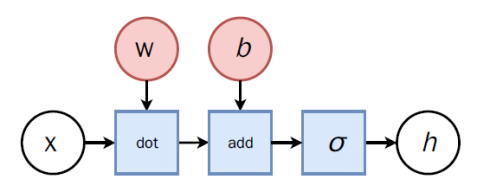
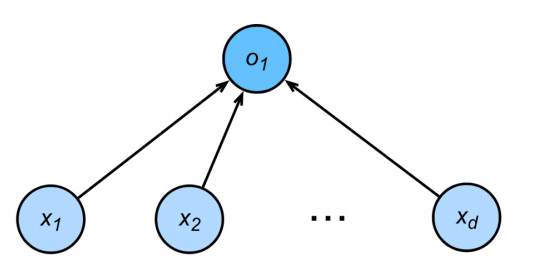
损失函数(loss)：$l(y,x,w)=max(0,-yw\cdot x)$其中y是真实label，为使损失函数最小，使用梯度下降算法（柯西，1860）
伪代码：

多层感知机MLP构成前向神经网络（全连接）：

单隐含层二分类

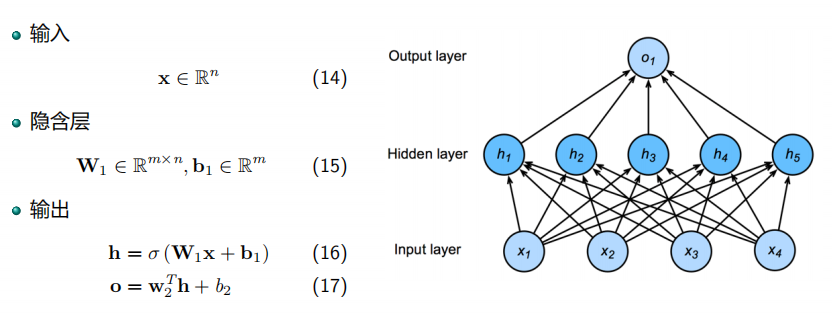
单隐含层多分类

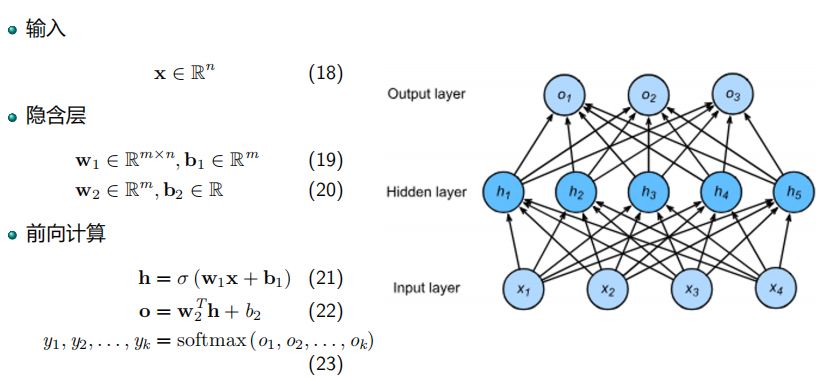
多隐含层多分类

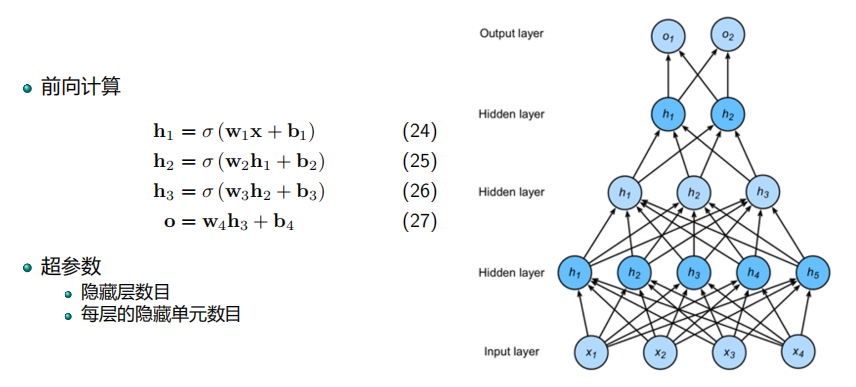
多层感知器具有对线性不可分数据进行辨识的能力

激活函数

作用
1.完成数据的非线性变换，解决线性模型的表达、分类能力不足的问题，而且如果网络中全是线性变换，那么可以通过数学推导转化为一层，失去了深度的含义；
2.执行数据的归一化，将输入数据映射到某个范围内，再往下传递，这样做的好处是可以限制数据的扩张，防止数据过大导致的溢出风险

激活函数的性质：
1.计算简单（频繁）
2.输出范围有限，如$\in [0,1]或[-1,1]$
3.非线性
4.单调性（保持梯度方向的稳定）
5.几乎处处可微（用于梯度下降算法的求导）

举例：
1.sigmoid函数
$sigmoid(x)=\frac{1}{1+e^{-x}}$
$sigmoi{d}^{\prime }(x)=sigmoid(x)(1-sigmoid(x))$

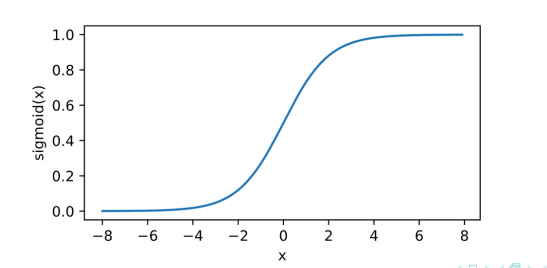
缺点：幂运算相对耗时；函数具有饱和性。在反向传播时容易出现梯度消失的情况，从而无法完成深层网络的训练；收敛缓慢
2.双曲正切函数
$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$
$tan{h}^{\prime }(x)=1-tan{h}^2(x)$

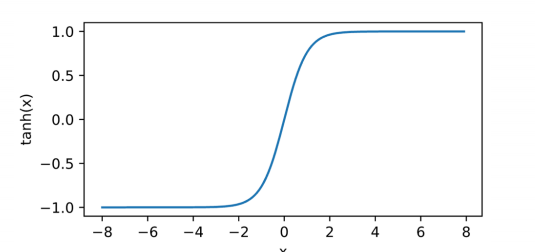
特点：和 Sigmoid 函数的曲线相近；在输入很大或是很小的时候，输出都几乎平滑；整个函数以 0 为中心；计算量大
3.线性修正函数(ReLU)
$ReLU(x)=max(x,0)$
$f^{\prime }(x)=1,x>0$

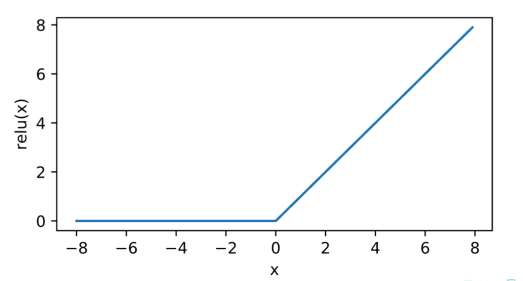
特点：仿生物学；解决梯度消失问题；计算比较简单
4.阶跃函数
$step(x)=\{\begin{array}{c}1,x>0\\ 0,x<0\end{array}$

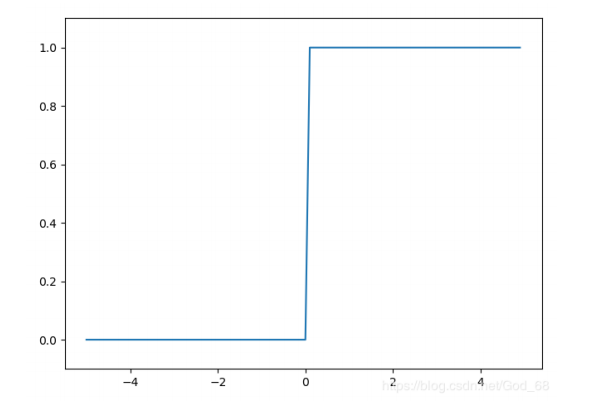
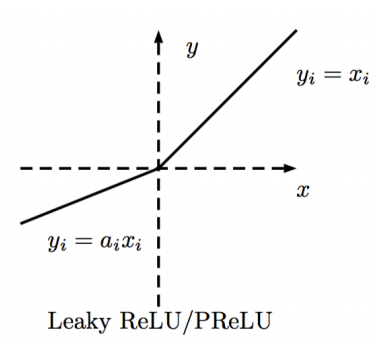
5.带泄露线性整流函数 (Leaky ReLU)
是 ReLU 函数的变体，输入值为负时梯度为一个常数

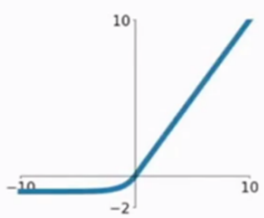
6.ELU 函数
$ELU(x)=\{\begin{array}{c}x,x>0\\ \alpha (e^x-1),x<=0\end{array}$
$EL{U}^{\prime }(x)=\{\begin{array}{c}1,x>0\\ ELU(x)+\alpha ,x<=0\end{array}$

7.SoftPlus 函数
ReLU 函数的平滑版,，值域为 (0, +∞)。运算量比较大，收敛速度比 ReLU 要慢很多
$f(x)=ln(e^x+1)$
$f^{\prime }(x)=\frac{1}{e^x+1}$

梯度下降算法

用于求函数的局部最小值

误差反向传播 (BP) 算法