算法学习——LeetCode力扣动态规划篇9

1035. 不相交的线
1035. 不相交的线 - 力扣(LeetCode)
描述
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足:
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例
示例 1:

输入:nums1 = [1,4,2], nums2 = [1,2,4]
输出:2
解释:可以画出两条不交叉的线,如上图所示。
但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出:3
示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出:2
提示
1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000
代码解析
动态规划
本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
那么本题就和我们刚刚讲过的这道题目动态规划:1143.最长公共子序列 就是一样一样的了。
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size()+1 , vector<int>(nums2.size()+1,0));for(int i=0 ; i<nums1.size();i++){for(int j=0 ; j<nums2.size();j++){if(nums1[i]==nums2[j])dp[i+1][j+1] = dp[i][j]+1;elsedp[i+1][j+1] = max(dp[i+1][j] , dp[i][j+1]);}}// for(int i=0 ; i<nums1.size();i++)// {// for(int j=0 ; j<nums2.size();j++)// {// cout<<dp[i][j]<<' ';// }// cout<<endl;// }return dp[nums1.size()][nums2.size()];}
};
53. 最大子数组和
53. 最大子数组和 - 力扣(LeetCode)
描述
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
示例
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示
1 <= nums.length <= 105
-104 <= nums[i] <= 104
代码解析
贪心算法
class Solution {
public:int maxSubArray(vector<int>& nums) {int sum=0 ,result= INT32_MIN; //sum是当前数组的和,result是sum中最大的时候for(int i=0 ; i<nums.size() ;i++){sum += nums[i]; //记录当前的sumif(sum > result) result= sum; //如果sum大于当前result,更新resultif(sum < 0) sum = 0; //某一个时期的sum小于0舍去}return result;}
};
动态规划
class Solution {
public:int maxSubArray(vector<int>& nums) {vector<int> dp(nums.size() ,0);int result = INT_MIN;dp[0]= nums[0];for(int i=1 ; i<nums.size() ;i++){dp[i] = max(nums[i],dp[i-1]+nums[i]);}for(int i=0 ; i<nums.size() ;i++) {// cout<<dp[i]<<' ';if(dp[i] > result) result = dp[i];}return result;}
};
392. 判断子序列
392. 判断子序列 - 力扣(LeetCode)
描述
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶
如果有大量输入的 S,称作 S1, S2, … , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
示例
示例 1:
输入:s = “abc”, t = “ahbgdc”
输出:true
示例 2:
输入:s = “axc”, t = “ahbgdc”
输出:false
提示
0 <= s.length <= 100
0 <= t.length <= 10^4
两个字符串都只由小写字符组成。
代码解析
动态规划
class Solution {
public:bool isSubsequence(string s, string t) {if(s.size()==0&&t.size()!=0) return true;if(s.size()==0&&t.size()==0) return true;if(s.size()!=0&&t.size()==0) return false;vector<bool> dp(s.size() , false);int prt = 0;//匹配指针for(int i=0 ; i<t.size() ;i++){if(s[prt] == t[i])//匹配成功标记,匹配下一个{dp[prt] = true;prt++;}}return dp[s.size()-1];}
};
115. 不同的子序列
115. 不同的子序列 - 力扣(LeetCode)
代码描述
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
示例
示例 1:
输入:s = “rabbbit”, t = “rabbit”
输出:3
解释:
如下所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
rabbbit
rabbbit
rabbbit
示例 2:
输入:s = “babgbag”, t = “bag”
输出:5
解释:
如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag
提示
1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成
代码解析
动态规划
-
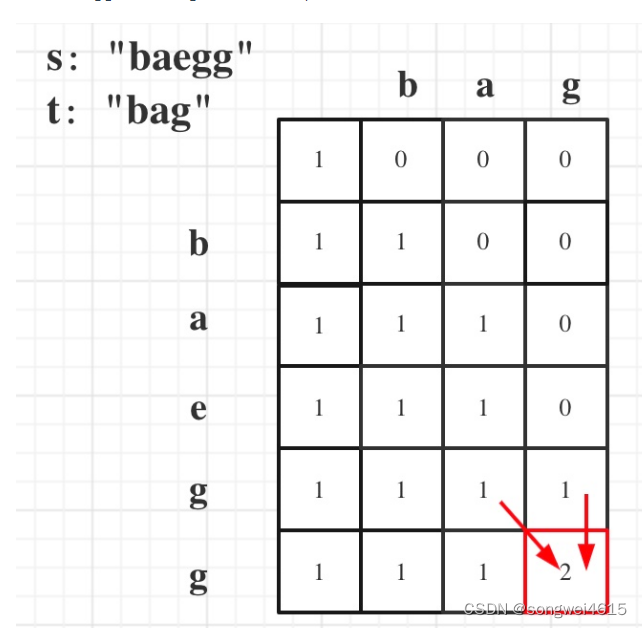
确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。 -
确定递推公式
这一类问题,基本是要分析两种情况- s[i - 1] 与 t[j - 1]相等
dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; - s[i - 1] 与 t[j - 1] 不相等
dp[i][j] = dp[i - 1][j];
- s[i - 1] 与 t[j - 1]相等
-
dp数组如何初始化
-
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。 -
再来看dp[0][j],dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。
那么dp[0][j]一定都是0,s如论如何也变成不了t。 -
最后就要看一个特殊位置了,即:dp[0][0] 应该是多少。
dp[0][0]应该是1,空字符串s,可以删除0个元素,变成空字符串t。
-
class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size()+1 , vector<uint64_t>(t.size()+1,0) );for(int i=1 ; i<s.size()+1 ;i++)dp[i][0] = 1;for(int j=1 ;j<t.size()+1 ;j++)dp[0][j] = 0;dp[0][0] = 1;for(int i=0 ; i<s.size() ;i++){for(int j=0 ;j<t.size();j++){if(s[i]==t[j]) dp[i+1][j+1] = dp[i][j] + dp[i][j+1];else dp[i+1][j+1] = dp[i][j+1];}}return dp[s.size()][t.size()];}
};




)
)



 消息)
函数的使用)
)







