💕"我们好像在池塘的水底,从一个月亮走向另一个月亮。。"💕
作者:Mylvzi
文章主要内容:算法系列–动态规划–回文子串系列
今天为大家带来的是
算法系列--动态规划--回文子串系列(1),本文重点掌握如何快速判断一个字符串是否是回文子串
一.回文子串(引入)
先来看力扣上这道题目:回文子串

1.利用动态规划的思想解决这道题目(重点)
回文子串其实是子数组的一种,只不过这里将数字换为字符而已,所以回文子串的问题也可以使用动态规划的思想解决,但是这个状态表示相较于常规的字符数组有些不同,在回文子串问题中,我们需要创建一个二维的dp表去存储所有子串是否是回文子串的信息,也就是说这个dp表是一个`boolean``类型的数组
首先如何得到所有的子字符串呢?很简单,两层for循环就能解决这个问题

注意:单独一个字符也算子字符串!!!
明确上述前置知识之后,下面讲解如何利用动态规划的思想解决回文子串问题
-
状态表示:dp[i][j]表示
以i下标为起始位置,j下标为结束位置的子字符串是否是回文子串的信息 -
状态转移方程:
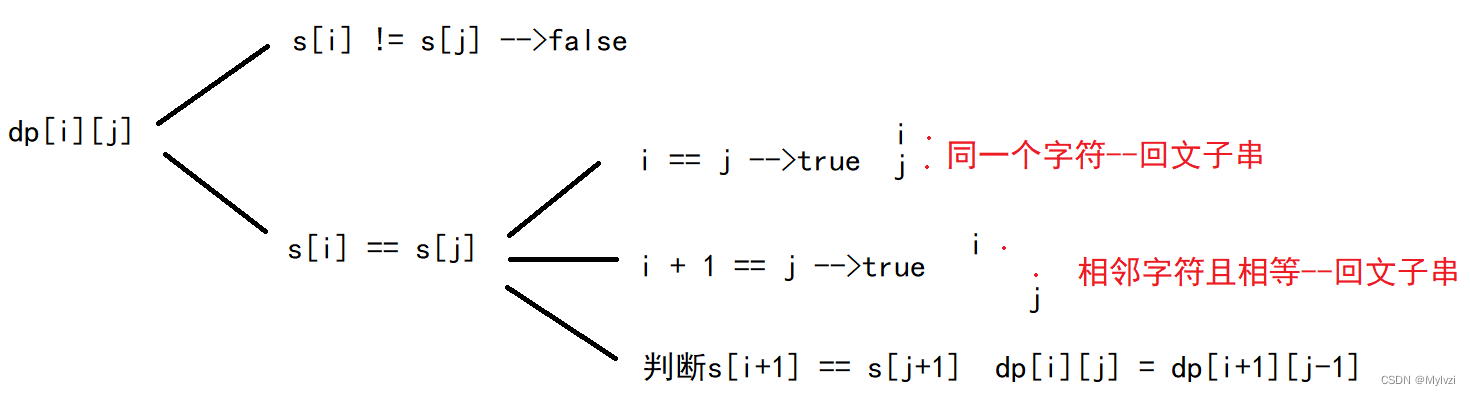
-
初始化:
无需初始化,越界的条件被特别判断了,不会出现越界的情况

-
填表顺序:
从下往上填

-
返回值:
dp[i][j]为true的数目
代码实现:
class Solution {public int countSubstrings(String s) {char[] ss = s.toCharArray();// 转化为字符数组int ret = 0;// 记录dp表中true的数目int n = s.length();boolean[][] dp = new boolean[n][n];for(int i = n - 1; i >= 0; i--) {// 从后往前遍历字符串for(int j = i; j < n; j++) {if(ss[i] == ss[j])// 只用判断相等的情况,不相等就是默认值false;dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;ret += dp[i][j] == true ? 1 : 0;}}return ret;}
}
如果使用动态规划,时间复杂度,空间复杂度均为为O(N^2)回文子串问题使用动态规划虽然不是最优解,但是可以实现一个非常重要的功能将所有子串是否是回文子串的信息,存储到dp表之中,最优解还有中心拓展算法和马拉车算法
中心拓展算法的实现:
链接:https://leetcode.cn/problems/palindromic-substrings/solutions/379987/hui-wen-zi-chuan-by-leetcode-solution/
来源:力扣(LeetCode)
class Solution {public int countSubstrings(String s) {int n = s.length(), ans = 0;for (int i = 0; i < 2 * n - 1; ++i) {int l = i / 2, r = i / 2 + i % 2;while (l >= 0 && r < n && s.charAt(l) == s.charAt(r)) {--l;++r;++ans;}}return ans;}
}
2.最长回文子串
链接:
https://leetcode.cn/problems/longest-palindromic-substring/
分析:
还是利用和上道题一样的动态规划思想,在本题中需要得到的是最长的回文子串,在回文子串的动态规划里,我们已经保存了所有的回文子串的信息,只要判断出来时回文子串,就更新一下长度即可
可以使用一个数组ret来记录字符串的起始结束位置
代码:
class Solution {public String longestPalindrome(String s) {char[] ss = s.toCharArray();int n = s.length();boolean[][] dp = new boolean[n][n];// 创建dp表int[] ret = new int[2];// 记录字符串的起始位置和结束位置for(int i = n - 1; i >=0; i --){for(int j = i; j < n; j++) {if(ss[i] == ss[j])dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;if(dp[i][j] == true) {if(j - i > ret[1] - ret[0]) {ret[0] = i;ret[1] = j;}}}}return s.substring(ret[0],ret[1] + 1);// 注意是"左闭右开"}
}
3.回⽂串分割IV
链接:
https://leetcode.cn/problems/palindrome-partitioning-iv/description/

分析:
- 其实题目的意思很简单,就是
判断字符串s能否分割为三个回文子串,最直观的想法就是暴力求解+判断是否是回文子串,而判断是否是回文子串已经在上面做过了

代码:
class Solution {public boolean checkPartitioning(String s) {char[] ss = s.toCharArray();// 转化为字符数组int ret = 0;// 记录dp表中true的数目int n = s.length();boolean[][] dp = new boolean[n][n];// 使用dp表保存所有的子字符串的信息for(int i = n - 1; i >= 0; i--) {// 从后往前遍历字符串for(int j = i; j < n; j++) {if(ss[i] == ss[j])// 只用判断相等的情况,不相等就是默认值false;dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;}}// 将字符串s分割为三个子字符串,分别判断是否是回文字符串for(int i = 1; i < n - 1; i++) {for(int j = i; j < n - 1; j++) {if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1])return true;}}return false;}
}
4.分割回⽂串II
链接:
https://leetcode.cn/problems/palindrome-partitioning-ii/description/

分析:
其实这道题和单词拆分很像,单词拆分中需要我们遍历整个字符串,判断对应的单词是否存在于字典之中,本题也是需要遍历整个字符串,判断对应的子字符串是否是回文子串,而判断是否是回文子串已经在上面介绍过

代码:
class Solution {public int minCut(String s) {char[] ss = s.toCharArray();// 转化为字符数组int ret = 0;// 记录dp表中true的数目int n = s.length();boolean[][] predp = new boolean[n][n];for(int i = n - 1; i >= 0; i--) {// 从后往前遍历字符串for(int j = i; j < n; j++) {if(ss[i] == ss[j])// 只用判断相等的情况,不相等就是默认值false;predp[i][j] = i + 1 < j ? predp[i + 1][j - 1] : true;}}// 下面是正题int[] dp = new int[n];for(int i = 0; i < n; i++) dp[i] = Integer.MAX_VALUE;// 初始化为最大值for(int i = 0; i < n; i++) {if(predp[0][i] == true) dp[i] = 0;// 0->i为回文串else {// 0->i不是回文串for(int j = 1; j <= i; j++) {if(predp[j][i]) dp[i] = Math.min(dp[i],dp[j - 1] + 1);}}}return dp[n - 1];}
}
5.最长回文子序列
链接:
https://leetcode.cn/problems/longest-palindromic-subsequence/
分析:
最先想到的状态表示就是以i位置为结尾字符串中的最长的回文子序列的长度,但是进一步分析发现此状态表示无法推导出状态转移方程,原因在于我们根本不能确定回文子序列,所以要更换一个状态表示
经过上述分析发现仅仅固定一个位置去表示字符串无法确定其回文子序列,所以需要两个下标来确定一个字符串(是不是和回文子串很像?),然后再去推导状态转移方程,只不过这里的状态相较于连续的子串更多一些,下面是详细的分析过程

代码:
class Solution {public int longestPalindromeSubseq(String s) {char[] ss = s.toCharArray();// 转化为字符数组int n = s.length();// 创建dp表int[][] dp = new int[n][n];dp[0][0] = dp[n - 1][n - 1] = 1;// 初始化int ret = 0;// 记录最大值for(int i = n -1; i >=0; i--) {for(int j = i; j < n; j++) {if(ss[i] == ss[j]) {if(i == j) dp[i][j] = 1;else if(i + 1 == j) dp[i][j] = 2;else dp[i][j] = dp[i + 1][j - 1] + 2;}else {dp[i][j] = Math.max(dp[i + 1][j],dp[i][j - 1]);}ret = ret > dp[i][j] ? ret : dp[i][j];// 更新最值}}return ret;}
}
6.让字符串成为回⽂串的最⼩插⼊次数(hard)
链接:
https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/description/
分析:
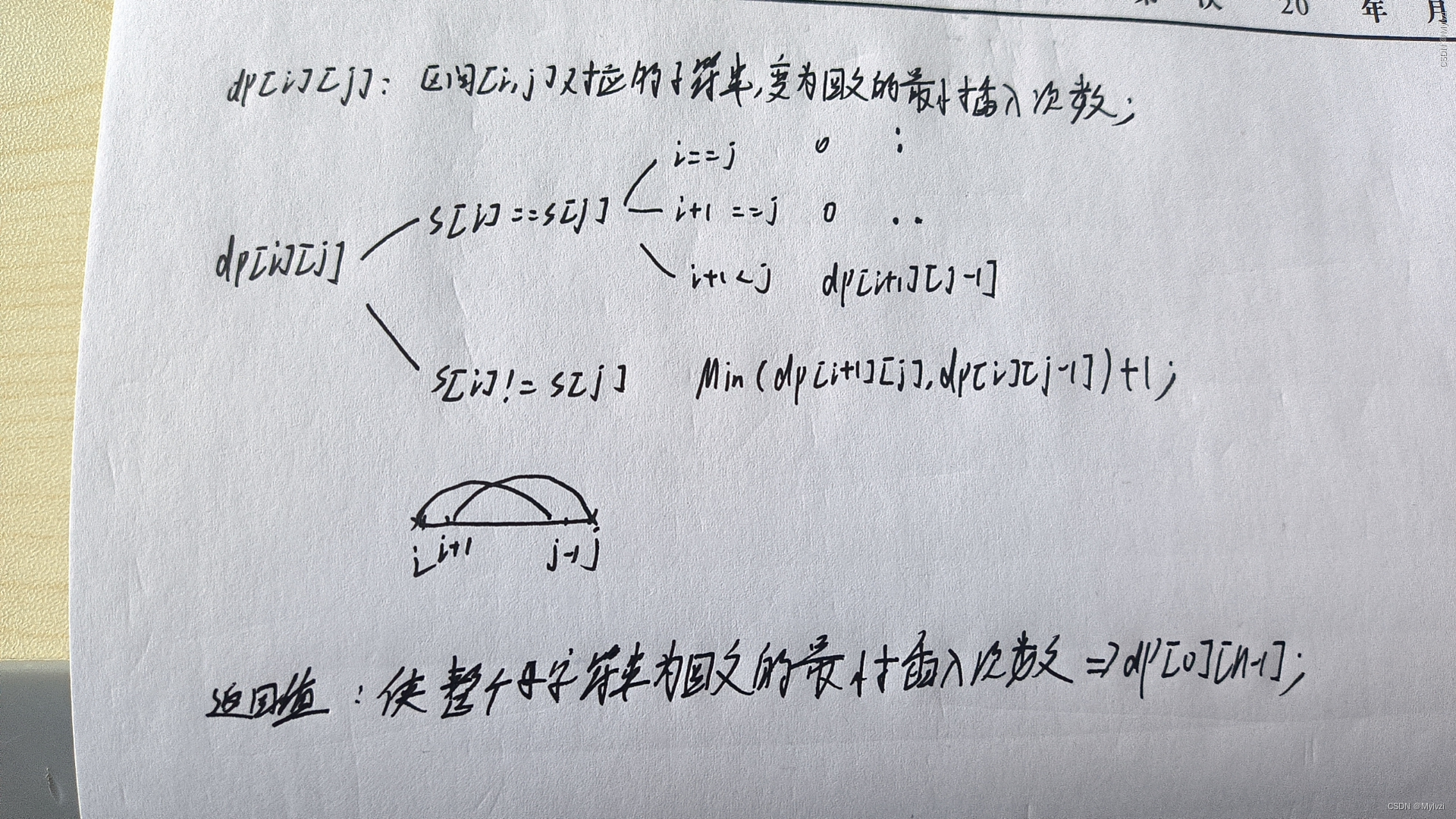
代码:
class Solution {public int minInsertions(String s) {char[] ss = s.toCharArray();// 转化为字符数组int n = s.length();// 创建dp表int[][] dp = new int[n][n];for(int i = n - 1; i >= 0; i--) {for(int j = i; j < n; j++) {if(ss[i] == ss[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : 0;else dp[i][j] = Math.min(dp[i + 1][j],dp[i][j - 1]) + 1;}}return dp[0][n - 1];}
}



)
)














交易触发定时器run_time)
