包子凑数（蓝桥杯，闫氏DP分析法）

题目描述：

小明几乎每天早晨都会在一家包子铺吃早餐。

他发现这家包子铺有 N 种蒸笼，其中第 i 种蒸笼恰好能放 Ai 个包子。

每种蒸笼都有非常多笼，可以认为是无限笼。

每当有顾客想买 X 个包子，卖包子的大叔就会迅速选出若干笼包子来，使得这若干笼中恰好一共有 X 个包子。

比如一共有 3 种蒸笼，分别能放 3、4和 5 个包子。

当顾客想买 11个包子时，大叔就会选 2 笼 3 个的再加 1 笼 5 个的（也可能选出 1 笼 3 个的再加 2 笼 4 个的）。

当然有时包子大叔无论如何也凑不出顾客想买的数量。

比如一共有 3 种蒸笼，分别能放 4、5和 6 个包子。

而顾客想买 7 个包子时，大叔就凑不出来了。

小明想知道一共有多少种数目是包子大叔凑不出来的。

输入格式:

第一行包含一个整数 N。

接下来 N 行，每行包含一个整数 Ai。

输出格式:

输出一个整数代表答案。

如果凑不出的数目有无限多个，输出INF。

数据范围:

1≤N≤100,
1≤Ai≤100

输入样例1：

2
4
5

输出样例1：

输入样例2：

2
4
6

输出样例2：

INF

样例解释

对于样例1，凑不出的数目包括：1, 2, 3, 6, 7, 11。
对于样例2，所有奇数都凑不出来，所以有无限多个。

前情提要：这道题目有关完全背包，01背包这两道题目，如果没看过这两道题目的题解大家可以去看看，能帮助理解这道题目。链接我也放到这里了，点击链接就行。

分析步骤：

第一：看到题目我们就能明白，每一笼包子是可以选无数多笼的，只要次数不超过我们指定的个数，看看能组合出多少种组合来，最后判断一下有多少个数组合出来了，多少个数没有组合出来那么这就是答案。由此可以得出第一个特点：题目是组合问题，是完全背包问题的变形：有几个物品，每个物品无限个，每个物品选任意个，能否凑到某个重量。

第二：我们如何判断这个题目是否有无数个值会组合不出来呢？我们想一下什么样的就组合不出来，例如2，4，6最大公约数是2所以奇数组合不出来，因为他只能组合出gcd的倍数。例如30，60最大公约数是30，所以只要不是30的倍数的就一定组合不出来，由此我们可以发现一些问题组合数和gcd有关，只要gcd不是1的话那么它就有无数种数组合不出来。这里用到裴蜀定理，任意两个数的组合必定是他们gcd的倍数，同样可以推广到更多数：如果这些数的gcd的d不是1那么有无数个数组合不出来

第三：闫氏DP分析法：

根据闫氏DP分析法我们可以知道dp问题可以将其分解为两个步骤：第一种是状态表示，第二种是状态计算。
我们所有的背包问题都是围绕我们对于集合的定义来的，所以这个定义是非常重要的！！！我们将集合定义为：所有只从前i个包子中选择，数量为j的集合是否能够达到题目要求的包子数，是个bool数组。
状态计算：由于完全背包是可以无限次的选择物品的，所以我们不能和01背包一样，只将其分解为选或者不选，因为它可以有很多很多种选择，可以不选，可以选一种，可以选两种...只要题目要求包子数量（背包体积）足够大就可以。
如果他不选择包子 i 那么这种情况相当于从（1，i - 1）中选择数量不超过j的情况是一样的所以我们的表达式是：f[i-1][j]。
如果他选择物品 i 那么这样又该如何表示呢？我们并不知道他到底要选择几个物品，那应该怎么做呢？假如我们选择一个的话那么就应该写为f[i-1][j-vi];假如我们选择两个的话那么就应该写为f[i-1][j-2*vi];假如我们选择k个的话那么就应该写为f[i-1][j-k*vi]，那么我们最终的答案就应该在这些集合之中。
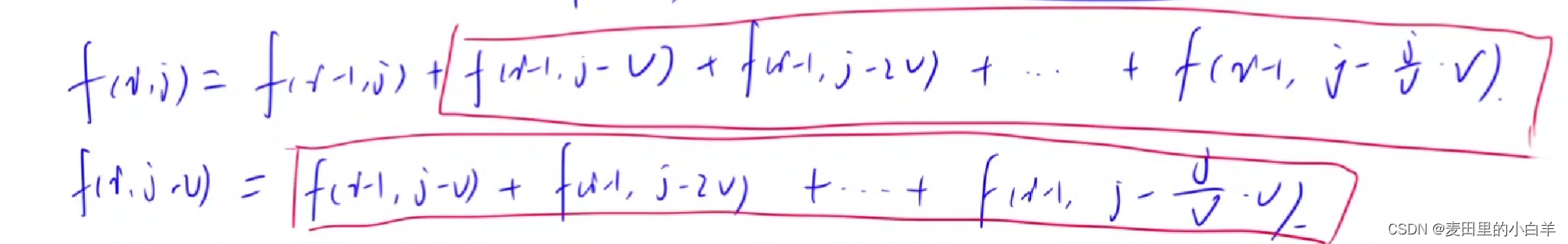
所以f(i,j) = f(i-1 , j) || f(i-1 , j - v) || f(i-1 , j - 2v) || ........|| f(i-1 , j - (j/v)*v);
所以f(i,j-v) = f(i-1 , j - v) || f(i-1 , j - 2*v) || f(i-1 , 3*v) || ........f(i-1 , j - (j/v)*v);
由上述两个式子，我们可以知道如果将 j 替换成 j-vi 两个式子非常相似。f[ i ] [ j ] = f[ i -1][ j ] || f[ i ][ j - vi ] ;

第四：书写主函数，构建整体框架：

输入值，并且根据裴蜀定理求出最大公约数看看是不是1，如果不是1那么必定有无数个值组合不出来，那么直接输出INF。初始化一下我们的f数组全部赋值为0，初始化我们的f[0][0] = true。为什么？根据我们对集合的定义来分析：只从前i个包子中选择，数量为j的集合是否能够达到题目要求的包子数。那么f[0][0]代表前0个包子中选择，数量为0的集合是可能的所以初始化为true。
```
for(int i = 1 ; i <= n ; ++ i){for(int j = 0 ; j <= 10000 ; ++ j){f[i][j] = f[i-1][j] || (j >= arr[i] ? f[i][j - arr[i]] : false) ;}}
```
d==1 的话我们就进入双重for循环。第一个for就是包子种类，第二个for就是包子数量。那么问题来了。我们怎么确定数量最大值就是10000呢？那么当qcd为1时，最大不能表示出来的数必定有个上界，因为两个数a，b(当gcd=1时)，最大不能表示出数是：(a-1)(b-1)-1。当数字更多的时候，这个上界必然更小(可选的数字变多了)，而99和98是100内最大的互质的数，所以这个上界选择10000。
我们之前分析出了f[ i ] [ j ] = f[ i -1][ j ] || f[ i ][ j - vi ] ;但是注意一个问题：选择一个，选择两个，是在所需包子数大于我们的这一笼包子数的情况下才可以选，假如所需包子数都要小于这一笼包子数的话就不可以选了！所以我们选择了用三目运算符 (j >= arr[i] ? f[i][j - arr[i]] : false) ;这句话的意思是如果 j >= arr[i] 是对的话那么则返回f[i][j - arr[i]] ；如果不对则返回false，那么f[ i ] [ j ] = f[ i -1][ j ] || f[ i ][ j - vi ]这就是错了就代表组合不出这个数。
最后我们只需要在遍历一遍，看看哪些数是组合不出来的，组合不出来就res++。

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110 ;int n ; 
bool f[N][10010];
int arr[N];int gcd(int a , int b){return b ? gcd(b,a%b):a;
}int main()
{cin>>n;int d = 0;for(int i = 1 ; i <= n ; ++i){cin>>arr[i];d = gcd(d,arr[i]);}memset(f, 0, sizeof f);f[0][0] = true;if(d != 1) cout<<"INF"<<endl;else{for(int i = 1 ; i <= n ; ++ i){for(int j = 0 ; j <= 10000 ; ++ j){f[i][j] = f[i-1][j] || (j >= arr[i] ? f[i][j - arr[i]] : false) ;}}int res = 0;for(int i = 0 ; i <= 10000 ; i ++){if(!f[n][i]) res ++;}cout<<res;
}return 0;
}