1.动态规划理论基础

1.1 什么是动态规划?

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。

1.2 动态规划的解题步骤

动态规划五部曲：

• 确定dp数组（dp table）以及下标的含义
• 确定递推公式
• dp数组如何初始化
• 确定遍历顺序
• 举例推导dp数组

2.斐波那契数

题目：

思路：
状态转移方程 dp[i] = dp[i - 1] + dp[i - 2]

代码：

class Solution:def fib(self, n: int) -> int:# 排除 Corner Caseif n == 0:return 0# 创建 dp table dp = [0] * (n + 1)# 初始化 dp 数组dp[0] = 0dp[1] = 1# 遍历顺序: 由前向后。因为后面要用到前面的状态for i in range(2, n + 1):# 确定递归公式/状态转移公式dp[i] = dp[i - 1] + dp[i - 2]# 返回答案return dp[n]

3.爬楼梯

题目：

思路：
递推公式dp[i] = dp[i - 1] + dp[i - 2]

代码：

class Solution:def climbStairs(self, n: int) -> int:if n == 1:return 1if n == 2:return 2dp = [0] * (n + 1)dp[1] = 1dp[2] = 2for i in range(3,n+1):dp[i] = dp[i - 2] + dp[i-1]return dp[n]

4.使用最小花费爬楼梯

题目：

思路：
dp[i]的定义：到达第i台阶所花费的最少体力为dp[i]。
递推公式：
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
注：楼顶的下标是n+1

代码：

class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:dp = [0] * (len(cost) + 1)# dp[0] = 0  # 初始值，表示从起点开始不需要花费体力# dp[1] = 0  # 初始值，表示经过第一步不需要花费体力for i in range(2, len(cost) + 1):# 在第i步，可以选择从前一步（i-1）花费体力到达当前步，或者从前两步（i-2）花费体力到达当前步# 选择其中花费体力较小的路径，加上当前步的花费，更新dp数组dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])return dp[len(cost)]  # 返回到达楼顶的最小花费

5.不同路径

题目：

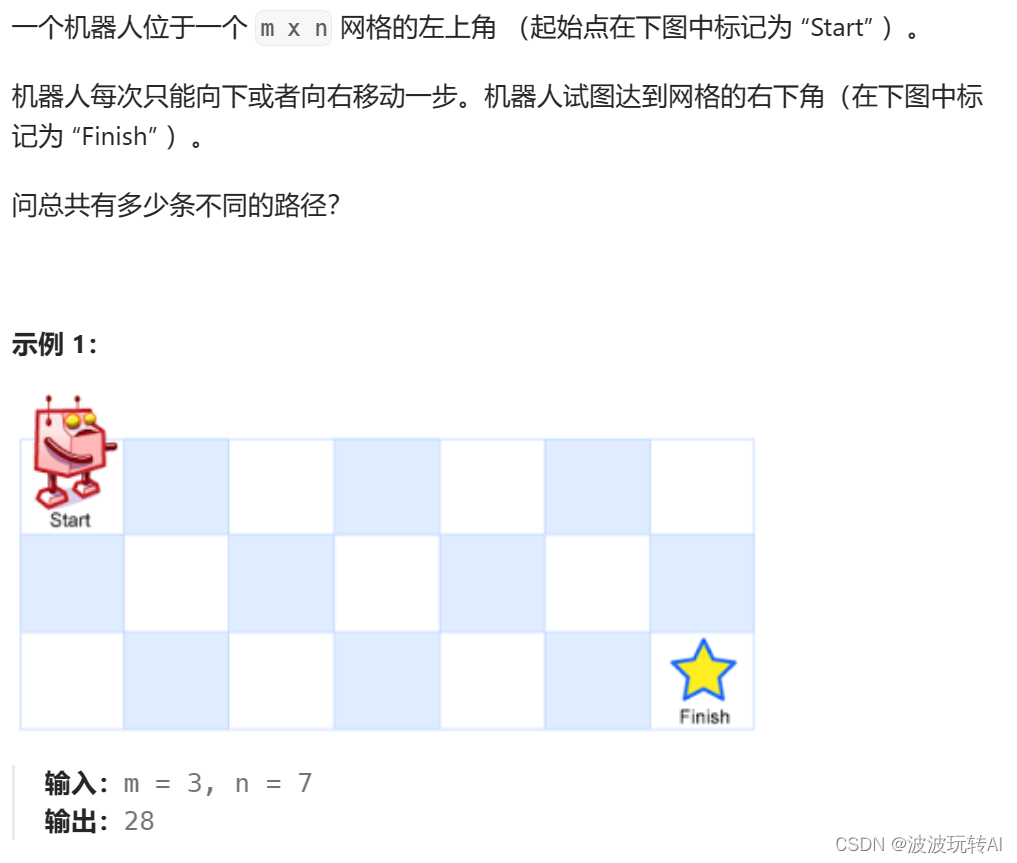
思路：
dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

递推公式：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。

代码：

class Solution:def uniquePaths(self, m: int, n: int) -> int:# 创建一个二维列表用于存储唯一路径数dp = [[0] * n for _ in range(m)]# 设置第一行和第一列的基本情况for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1# 计算每个单元格的唯一路径数for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]# 返回右下角单元格的唯一路径数return dp[m - 1][n - 1]

6.不同路径 II

题目：

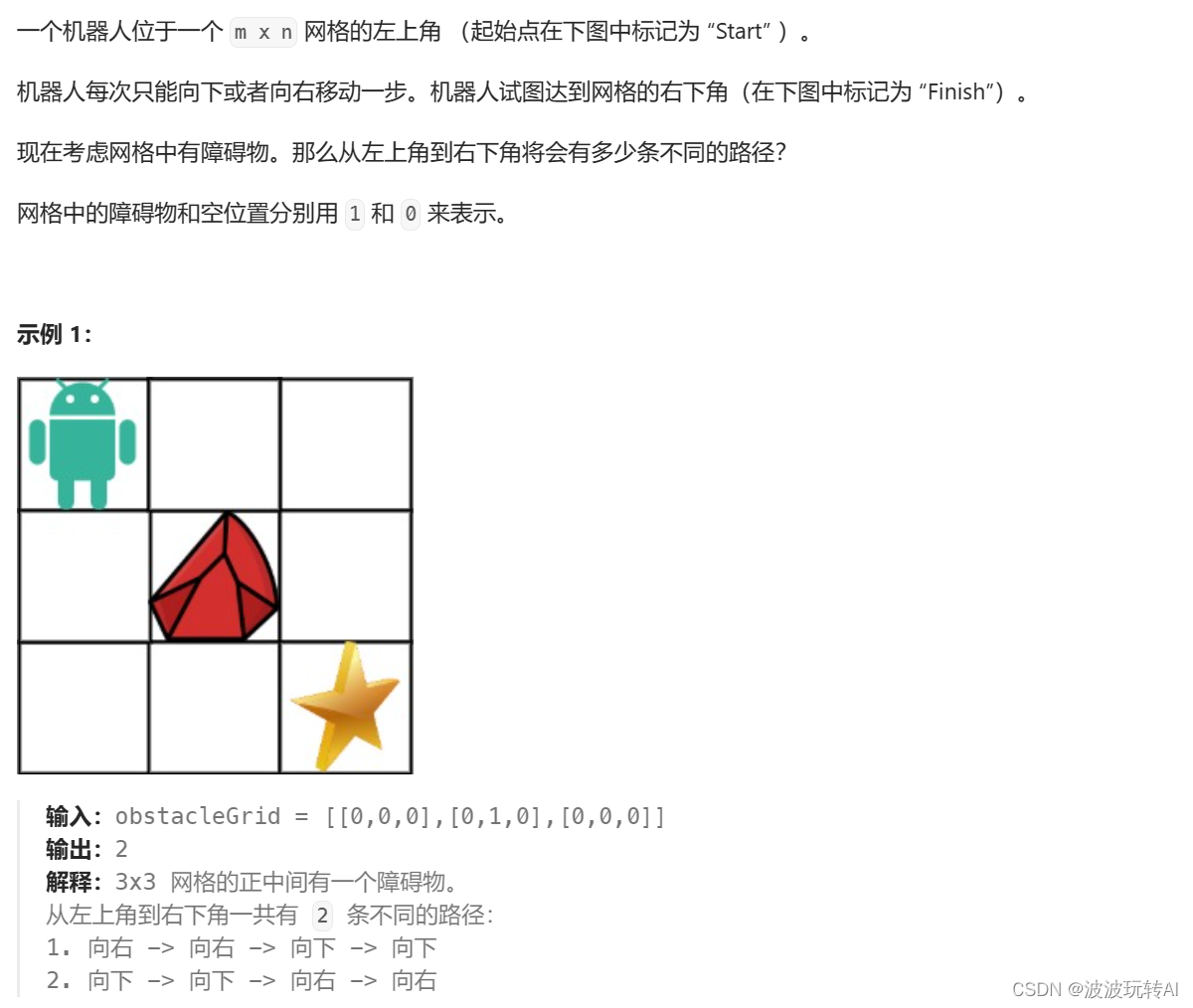
思路：
【注】边界初始化时要注意障碍物，还要考虑到起始点和终止点的障碍物
当网格中没有障碍物时，执行递推公式。

代码：

class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m = len(obstacleGrid)n = len(obstacleGrid[0])if obstacleGrid[0][0] == 1 or obstacleGrid[m - 1][n - 1] == 1:return 0dp = [[0] * n for _ in range(m)]i = 0j = 0while i < m and obstacleGrid[i][0] != 1:dp[i][0] = 1i += 1while j < n and obstacleGrid[0][j] != 1:dp[0][j] = 1j += 1for i in range(1,m):for j in range(1,n):if obstacleGrid[i][j] != 1:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[m-1][n-1]

7. 整数拆分

题目：

思路：
dp[i]：分拆数字i，可以得到的最大乘积为dp[i]

递推公式：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});

代码：

class Solution:def integerBreak(self, n: int) -> int:dp = [0] * (n + 1)for i in range(2,n+1):j = 1while j <= i // 2:dp[i] = max(j * (i - j),j*dp[i - j],dp[i])j += 1return dp[n]

8. 不同的二叉搜索树

题目：

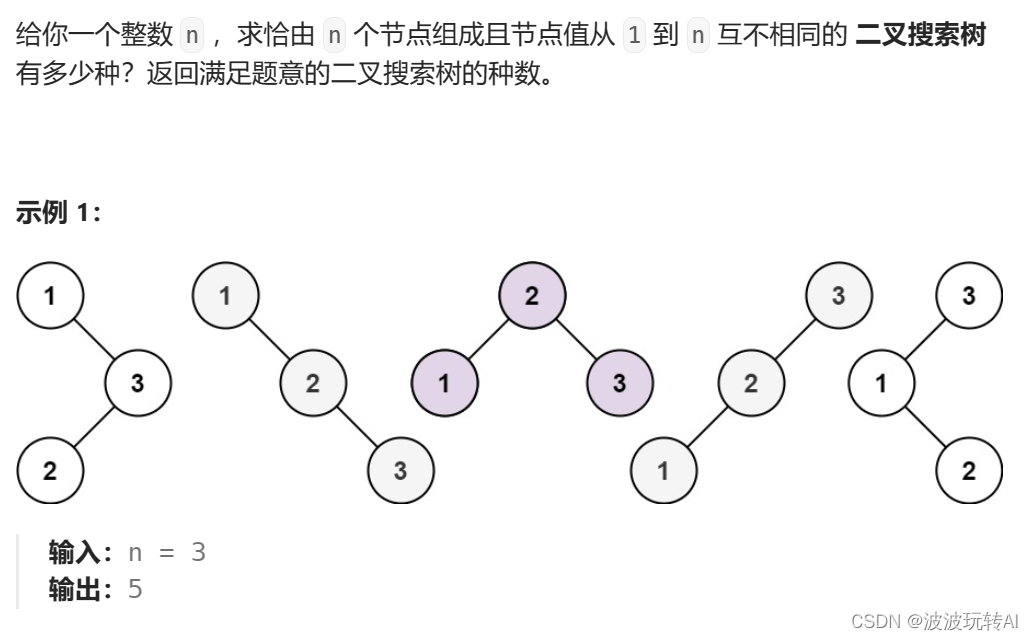
思路：
思路详解

代码：

class Solution:def numTrees(self, n: int) -> int:dp = [0] * (n + 1)  # 创建一个长度为n+1的数组，初始化为0dp[0] = 1  # 当n为0时，只有一种情况，即空树，所以dp[0] = 1for i in range(1, n + 1):  # 遍历从1到n的每个数字for j in range(1, i + 1):  # 对于每个数字i，计算以i为根节点的二叉搜索树的数量dp[i] += dp[j - 1] * dp[i - j]  # 利用动态规划的思想，累加左子树和右子树的组合数量return dp[n]  # 返回以1到n为节点的二叉搜索树的总数量