15 光线追踪（辐射度量学、BRDF与渲染方程）

基于物理渲染的基础知识

摘要

本篇文章将会从基于物理渲染(PBR)的动机开始讲起，逐步介绍PBR相关的基础知识，如辐射度量学(怎么用物理量精确的描述光线)，以及通过辐射度量学从而定义出来的BRDF(Bidirectional Reflectance Distribution Function)，最后会给出渲染方程，以及它直观的物理解释，帮助理解。

1 为什么需要辐射度量学？

首先，想一想到目前为止我们对光线亮度的定义是什么？只是简单的用3维(R,G,B)向量来描述，但却没有任何的单位，如果想要一个完全正确的模型，这显然是不应该的，必须用合适的物理量来描述光线！

其次，考虑在前两篇文章中提到的whited-style光线追踪模型，它真的是一个正确的模型吗？显然不是，原因如下：

1 whited-style光线追踪并没有对漫反射的光线进行追踪，而是直接返回当前着色点颜色

2 在计算光源直接照射的贡献时，使用了Blinn-Phong模型，而Blinn-Phong模型本身就是一个不准确的经验模型，使用的这种模型的whited-style光线追踪自身自然也是不正确的

而就以上的各种缺点而言，所有的问题都能在辐射度量学之中得到完美解决！

2 辐射度量学

辐射度量学其实是对光照的一套测量系统和单位，它能够准确的描述光线的物理性质。

具体来说，我们需要明白的是其中的几个关于光线的概念，分别为： 辐射能量(Radiant energy)，辐射通量(Radiant flux)，辐射强度(Radiant intensity)，irradiance，radiance，(对后两种概念没有合适的中文，所以就直接用英文了)，接下来就对这些概念进行具体解释。

2.1 辐射能量(Radiant energy)和辐射通量(Radiant flux)

首先看一看Radiant energy的定义：

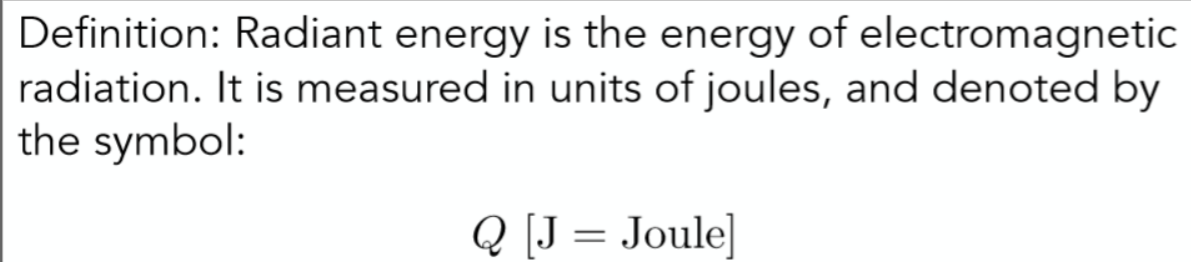
所谓辐射能量其实非常直观，就是辐射出来的电磁能量，单位为焦耳。可以用物理当中的做功的大小来进行类比。

接下来是Radiant flux(power)：

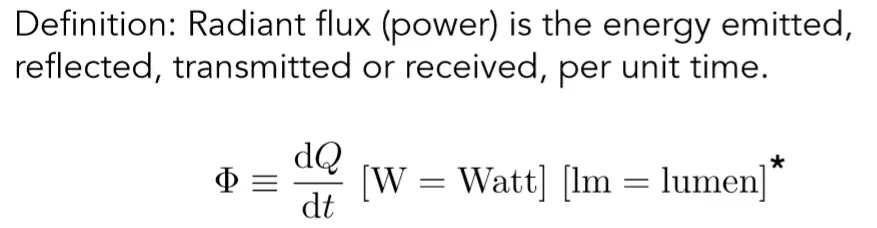
所谓辐射通量或者说辐射功率，其实就是在辐射能量的基础之上除以时间，也就是单位时间的能量。同样也可以用物理当中的功率来进行类比。

(tips: 具体来说一般偏向用radiant flux来衡量光线的亮度，因为我们更关心的是单位时间的效果，事实上也是这么做的，想想在说白炽灯泡的时候也是说60W亮度，80W亮度)

2.2 辐射强度(Radiant intensity)

在进行具体的数学定义之前，先借助如下一张图建立对剩下3个概念的一些直观的理解：

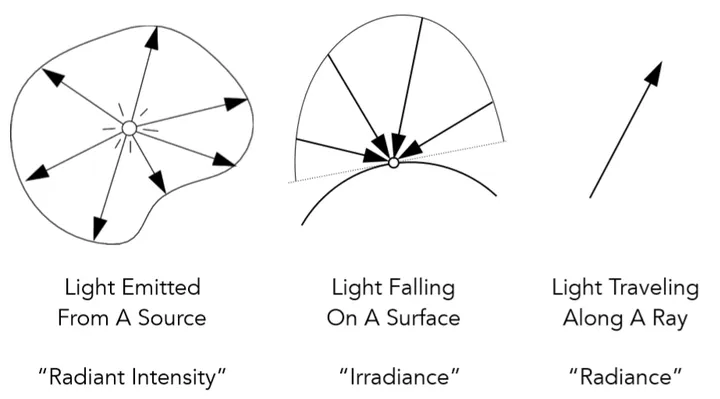
1 Radiant itensity其实就是指从一个光源出发某一方向上的亮度

2 Irradiance指某一微小平面所接受到的光线亮度

3 radiance衡量的是一条传播光线所具有的亮度(不受传播方向影响而改变)

（这里的亮度也可以理解为radiant flux(power)。）

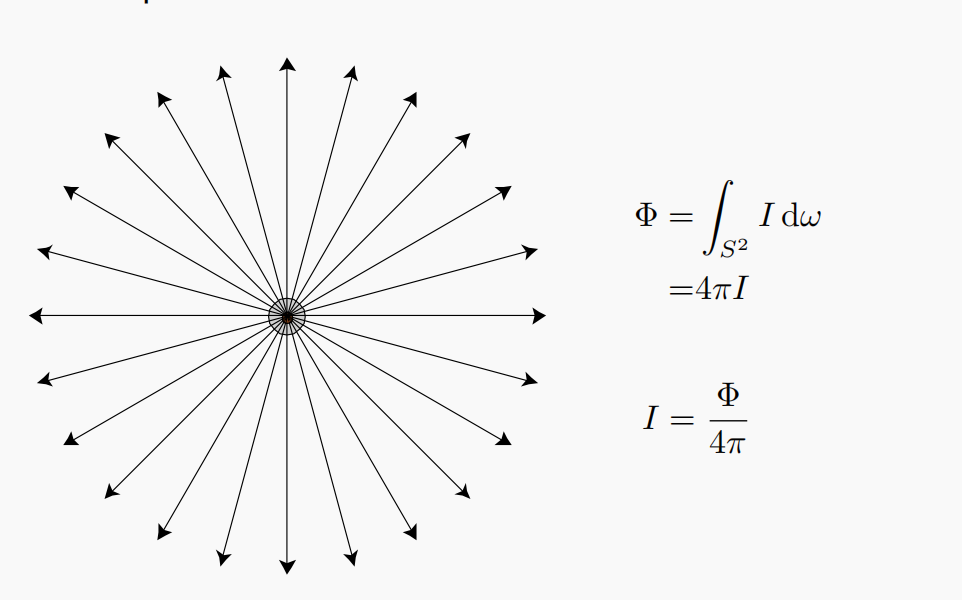
好了，接下来首先看Radiant intensity的数学定义：

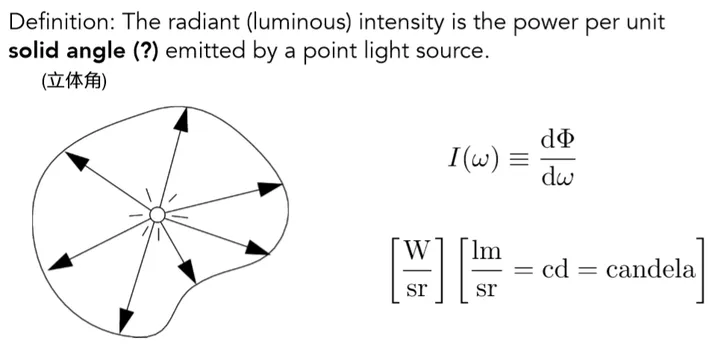
Radiant intensity一句话来说就是从光源发出的每单位立体角上的功率，关于辐射功率的定义在上文已经解释，这里唯一还不知道的就是立体角(solid angle)了。

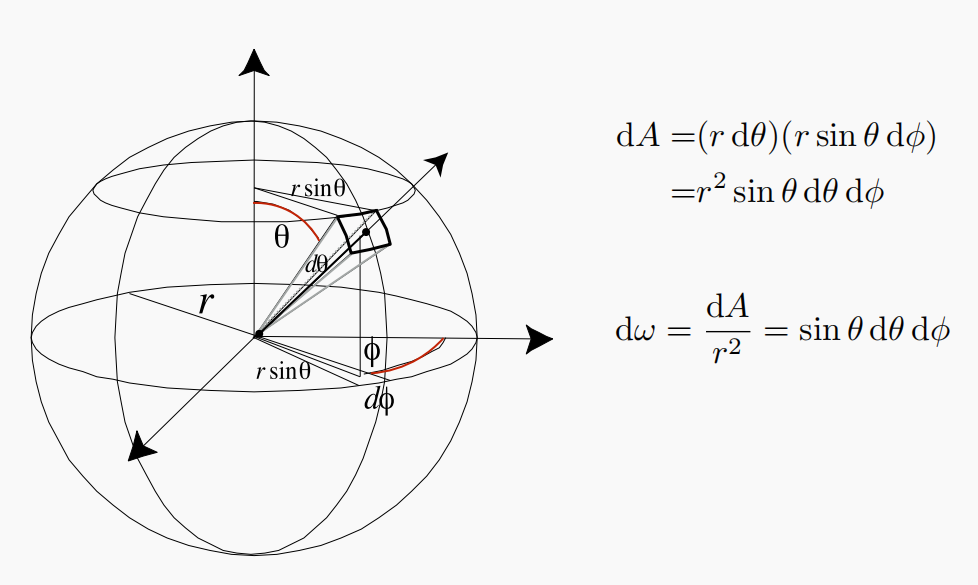
solid angle其实就是对应二维空间中圆的弧度在三维空间中球上的拓展。 首先看在二维计算弧度公式如下：

即立体角度所对应球上的投影面积比上半径的平方，整个球的立体角为4PI。

那么对于Radiant intensity的定义当中，微分立体角dw计算如下：

2.3 irradiance

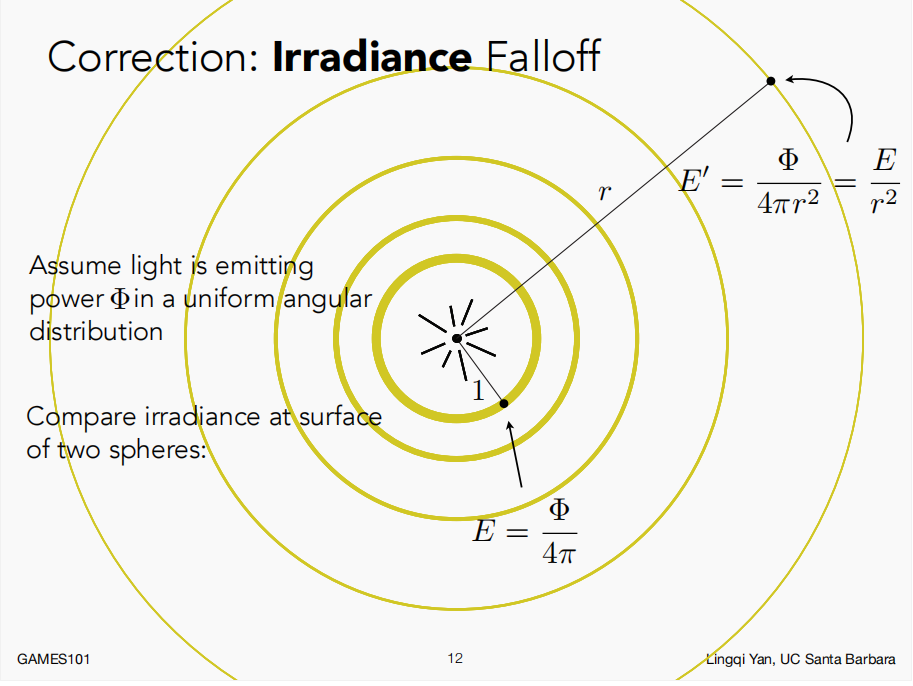
该现象也完全可以用irradiance解释，因为光的功率始终一致，离点光源所照射到的圆球面积也就越大，因此根据irradiance的式子，分母的面积值也就越大，irradiance也就越小。

2.4 radiance

最后，我们终于来到了最后一条概念了，这条概念也是所有辐射度量学的概念当中最为重要的一个，那么首先直接就来看他的数学定义是怎么样的：

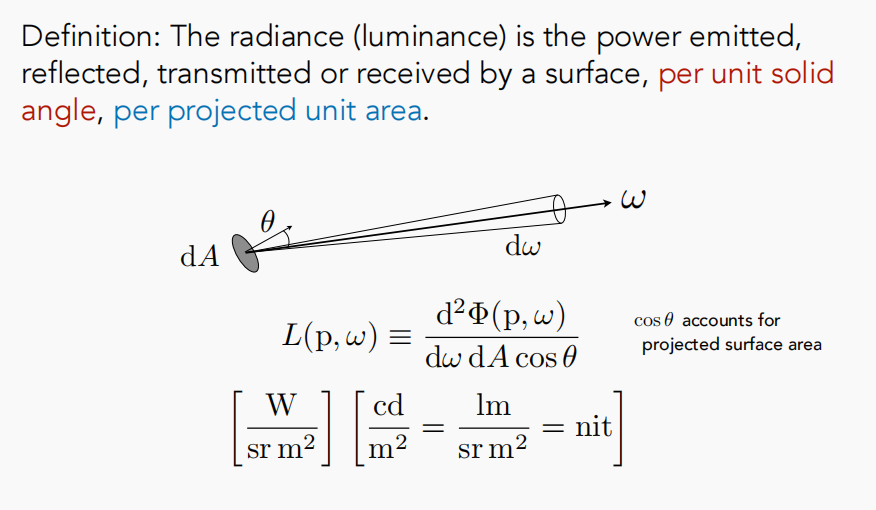
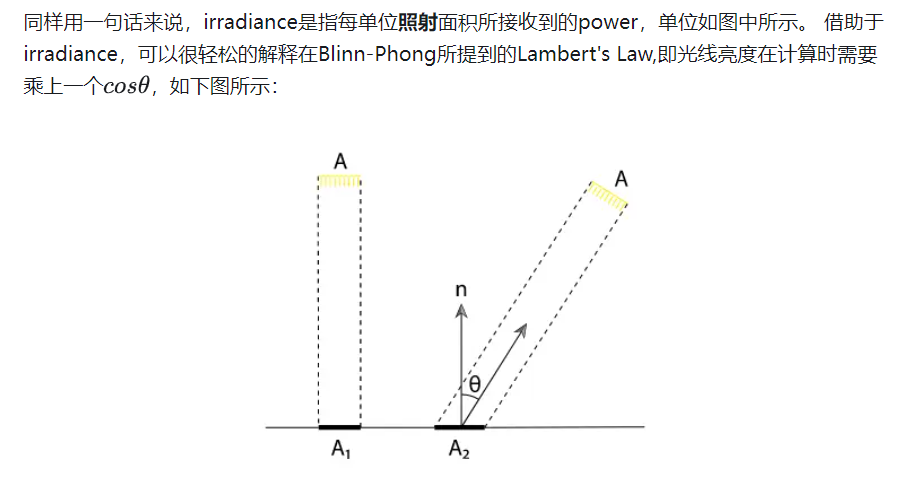
用一句话概述的话，所谓radiance就是指每单位立体角，每单位垂直面积的功率，直观来看的话，很像是Intensity和irradiance的结合。它同时指定了光的方向与照射到的表面所接受到的亮度

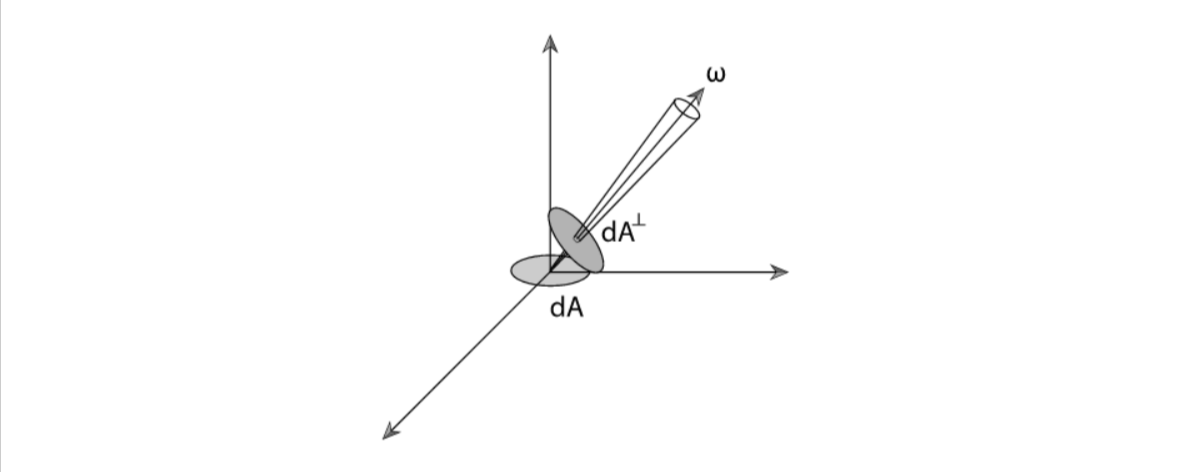
但这里有一个细微的区别，在irradiance中定义的每单位照射面积，而在radiance当中，为了更好的使其成为描述一条光线传播中的亮度，且在传播过程当中大小不随方向改变，所以在定义中关于接收面积的部分是每单位垂直面积，而这一点的不同也正解释了图中式子分母上的cosθ，具体可以观察如下图：

3 双向反射分布函数(BRDF)

通过上述所有辐射度量学各种概念的定义之后，我们可以从这样一个角度理解光线的反射，如下图所示：

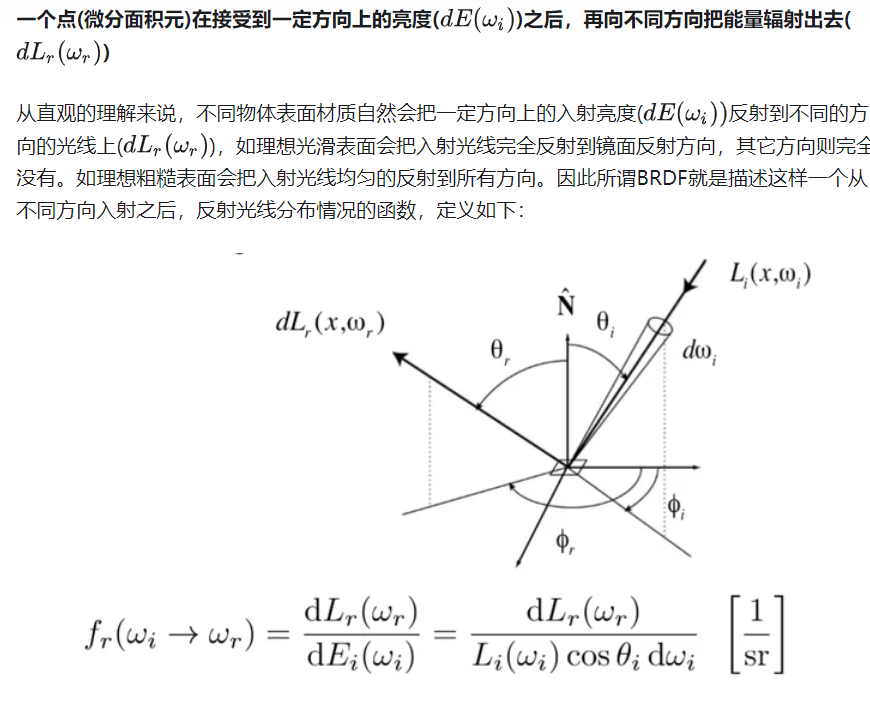
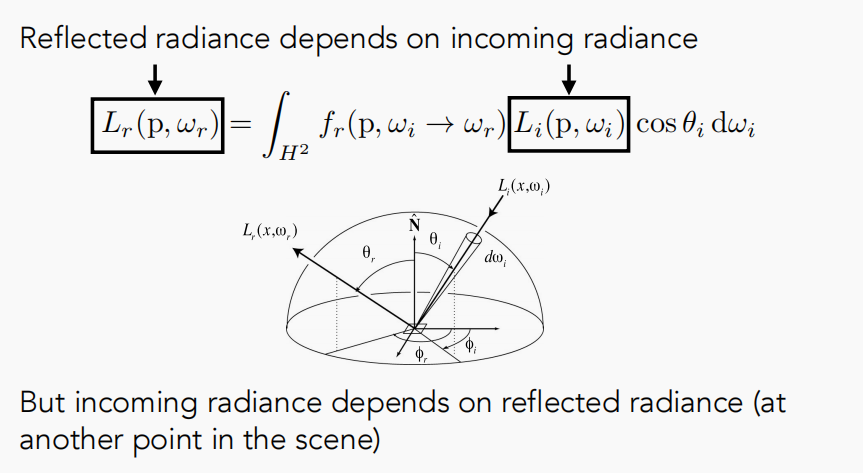
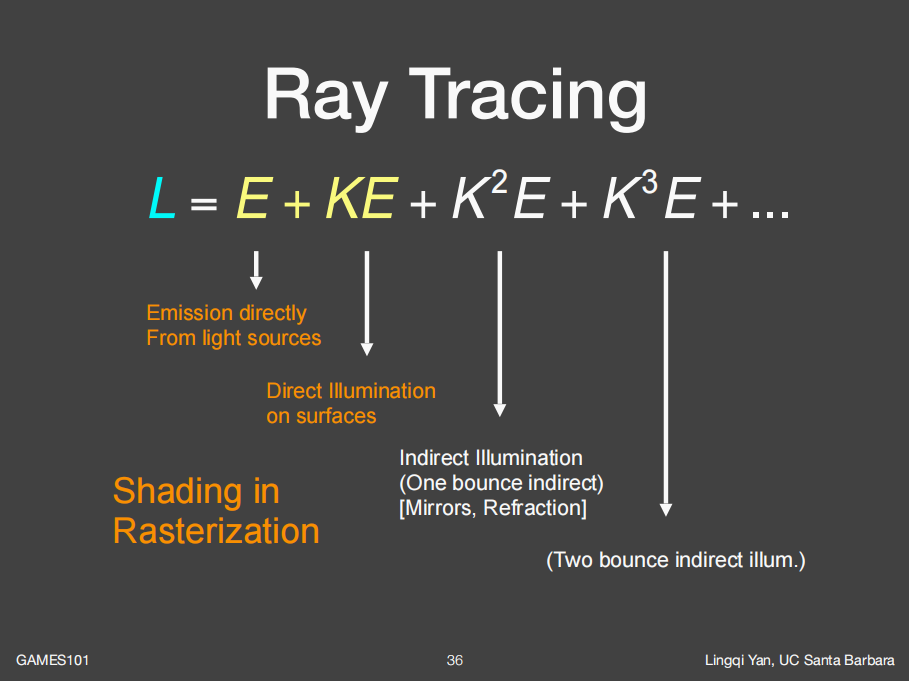
不难发现正如上图中所说的，入射光线的radiance不仅仅是光源所引起的，还有可能是其他物体上着色点的反射光线的radiance，恰好反射到当前的着色点p(即间接光照)，同时其他物体上的反射光线的radiance依然也是由直接光照和间接光照构成，因此这与whitted-style当中的光线追踪过程十分类似，也是一个递归的过程。所以说想要解这样一个方程还是比较难的。

接下来，在最后一章我们会引入渲染方程，并对渲染方程做一些直观上的物理解释，对于反射方程或者说是渲染方程的具体求解，留在下一篇文章里面去说。

4 渲染方程及其物理含义解释

(点光源对一个点来说自然只有一个方向有入射光，所以这里没有了积分)

多个点光源一个物体的情况：

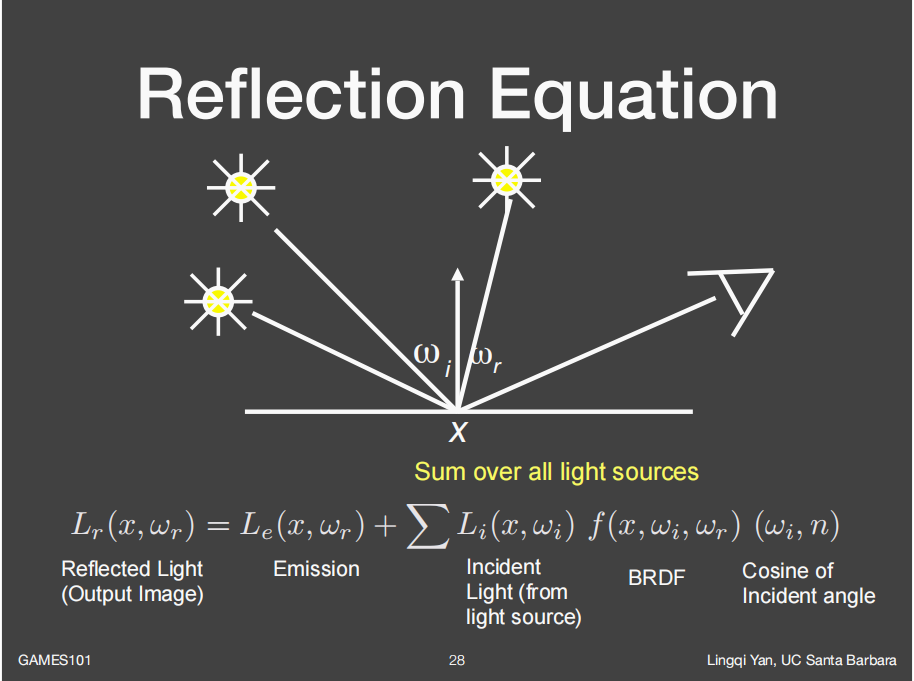
将这些所有的点光源的贡献全部求和即可，那么如果点光源变成了面光源呢？如下图所示：

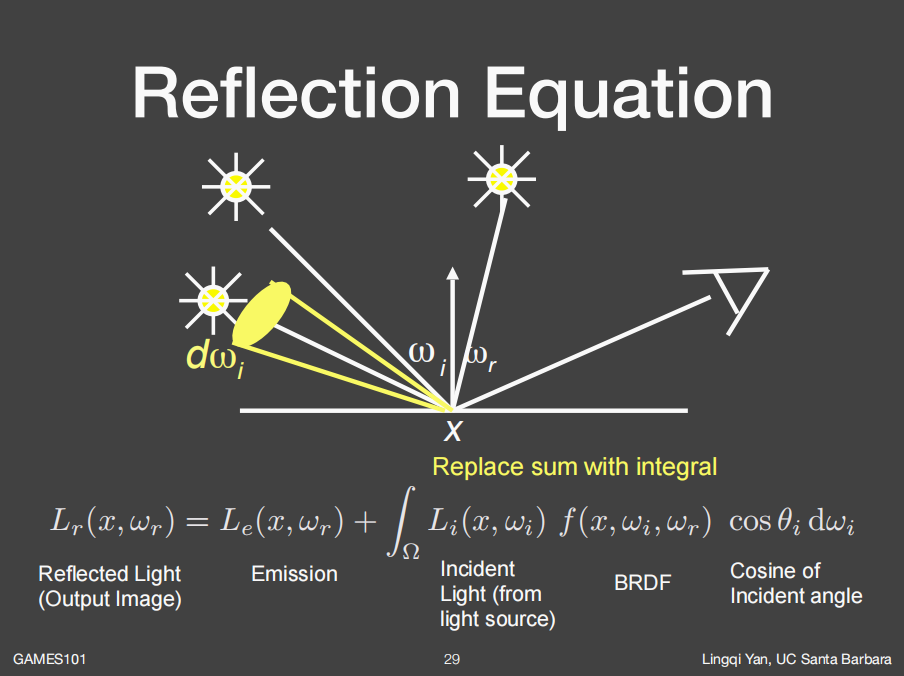
其实面光源就相当于无穷多个点光源的集合，只需要对 面光源所在的立体角范围进行积分，并且能够确定不同立体角方向的面光源的入射光radiance即可。

那么更进一步的，再在场景当中加入其它物体，使得物体之间发生光线交互之后是什么情况呢：

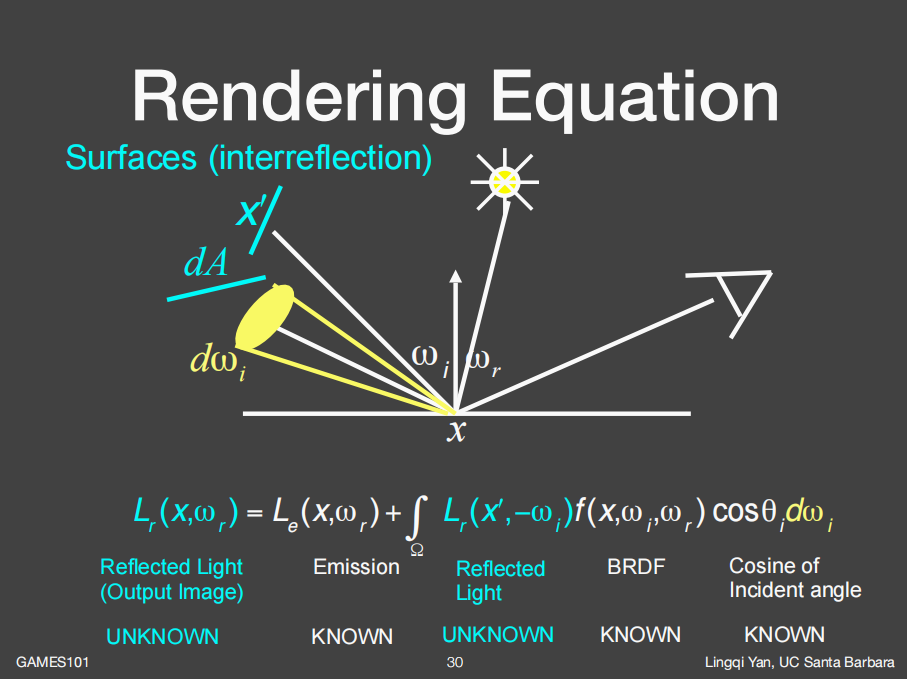
如上图所示，可以把其它物体同样考虑成面光源，对其所占立体角进行积分即可，只不过对其它物体的立体角积分不像是面光源所有入射方向都有radiance，物体的立体角可能只有个别几个方向有入射的radiance(即多次物体间光线反射之后恰好照射到着色点x)，其它方向没有，但本质上都可以视作是面光源。

观察一下图中的渲染方程可以发现除了两个radiance，其它所有项都是知道的，可以将上式进一步写成如下图下方所示的式子：

其中各项与原渲染方程中一一对应，(这里其实是有数学严格推导的，不过我们只是为了接下来构建直观的物理解释，对于这些推导不必在意，默认成立即可)，再接着，可以把该式子离散化写为线性代数的形式：

最后以几张基于物理渲染的图片作为本篇文章的结束 一次反射直接光照：

(考虑次数越多越接近真实图片效果,趋近收敛)

总结

以上就是所有的关于PBR的一些相关基础知识了，我们从辐射度量学入手，掌握了正确衡量光线属性的方法，由此定义出了BRDF，来表示物体的材质，即它对于光线的反射能量分布，最后结合辐射度量学与BRDF得到渲染方程，一个个真正完全正确的光线传播模型！