一.题目要求
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
二.题目难度
中等
三.输入样例
示例 1:
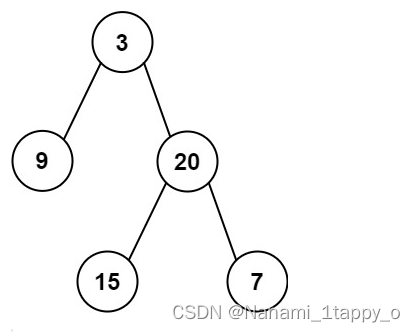
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- -3000 <= preorder[i], inorder[i] <= 3000
- preorder 和 inorder 均 无重复 元素
- inorder 均出现在 preorder
- preorder 保证 为二叉树的前序遍历序列
- inorder 保证 为二叉树的中序遍历序列
四.解题思路
没有思路 看GPT总结吧
五.代码实现
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {return buildTreeHelper(preorder, 0, preorder.size(), inorder, 0, inorder.size());}private:TreeNode* buildTreeHelper(vector<int>& preorder, int preStart, int preEnd, vector<int>& inorder, int inStart, int inEnd) {if (preStart >= preEnd || inStart >= inEnd) {return nullptr;}TreeNode* root = new TreeNode(preorder[preStart]);auto rootPos = find(inorder.begin() + inStart, inorder.begin() + inEnd, preorder[preStart]);int leftSize = rootPos - (inorder.begin() + inStart);root->left = buildTreeHelper(preorder, preStart + 1, preStart + 1 + leftSize, inorder, inStart, inStart + leftSize);root->right = buildTreeHelper(preorder, preStart + 1 + leftSize, preEnd, inorder, inStart + 1 + leftSize, inEnd);return root;}
};
六.题目总结
构造二叉树的问题可以通过递归的方法解决,核心思路是利用先序遍历和中序遍历的特性:
- 先序遍历(preorder)的特点是每次遍历的第一个元素都是当前子树的根节点。
- 中序遍历(inorder)的特点是根节点将树分为左子树和右子树,左子树的节点都在根节点的左边,右子树的节点都在根节点的右边。
解题步骤
- 步骤 1: 确定根节点
从先序遍历的数组中获取第一个元素,这个元素是当前子树的根节点。
- 步骤 2: 分割中序遍历数组
在中序遍历的数组中找到根节点的位置,这个位置将数组分为两部分:左子树的中序遍历和右子树的中序遍历。
- 步骤 3: 分割先序遍历数组
利用中序遍历中左子树的节点数,可以确定先序遍历数组中左子树和右子树的分界线。
第一个元素后面紧跟着的是左子树的先序遍历,接着是右子树的先序遍历。
- 步骤 4: 递归构建子树
使用步骤 2 和步骤 3 中确定的左右子树的先序遍历和中序遍历数组,递归地构建左子树和右子树。
- 步骤 5: 返回根节点
将构建好的左右子树分别连接到根节点的左右指针上,然后返回根节点。
示例
假设我们有以下先序遍历和中序遍历的数组:
- preorder = [3,9,20,15,7]
- inorder = [9,3,15,20,7]
先序遍历的第一个元素是3,所以3是根节点。
在中序遍历数组中找到3,它将数组分为两部分:
- [9]是左子树的中序遍历,[15,20,7]是右子树的中序遍历。
由于左子树在中序遍历中有1个节点,我们知道先序遍历数组中第一个元素之后的一个元素(9)是左子树的先序遍历;剩下的[20,15,7]是右子树的先序遍历。
-
对于左子树,先序遍历和中序遍历都只有一个元素[9],这意味着左子树只有一个节点9。
-
对于右子树,我们重复上述过程,先序遍历[20,15,7]和中序遍历[15,20,7],可以构建出右子树。
-
将构建好的左右子树连接到根节点3上。
通过这个过程,我们能够逐步构建出整棵树。






】pytorch 里的log_softmax, nll_loss, cross_entropy的关系)
提取图像中水平线和垂直线的opencv示例)


 for python 3.6/python3.X增强补丁)








