过拟合欠拟合面试题
1. 如何理解高方差与低偏差?
模型的预测误差可以分解为三个部分: 偏差(bias), 方差(variance) 和噪声(noise).
偏差
- 偏差度量了模型的期望预测与真实结果的偏离程度, 即刻画了学习算法本身的拟合能力。偏差则表现为在特定分布上的适应能力,偏差越大越偏离真实值。
方差
- 方差度量了同样大小的训练集的变动所导致的学习性能的变化, 即刻画了数据扰动所造成的影响。方差越大,说明数据分布越分散。
噪声
-
噪声表达了在当前任务上任何模型所能达到的期望泛化误差的下界, 即刻画了学习问题本身的难度 。
下图为偏差和方差示意图。
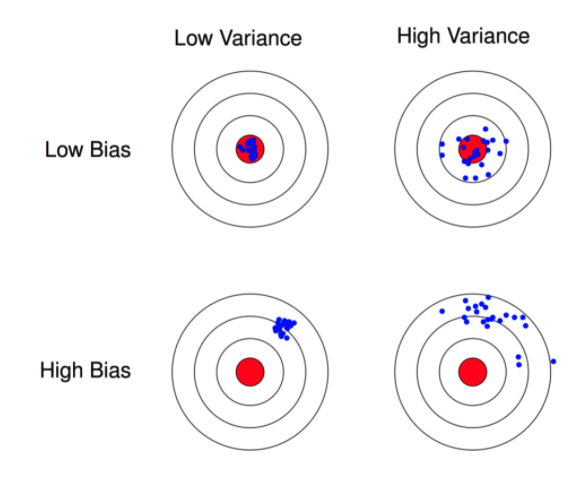
泛化误差、偏差、方差和模型复杂度的关系(图片来源百面机器学习)
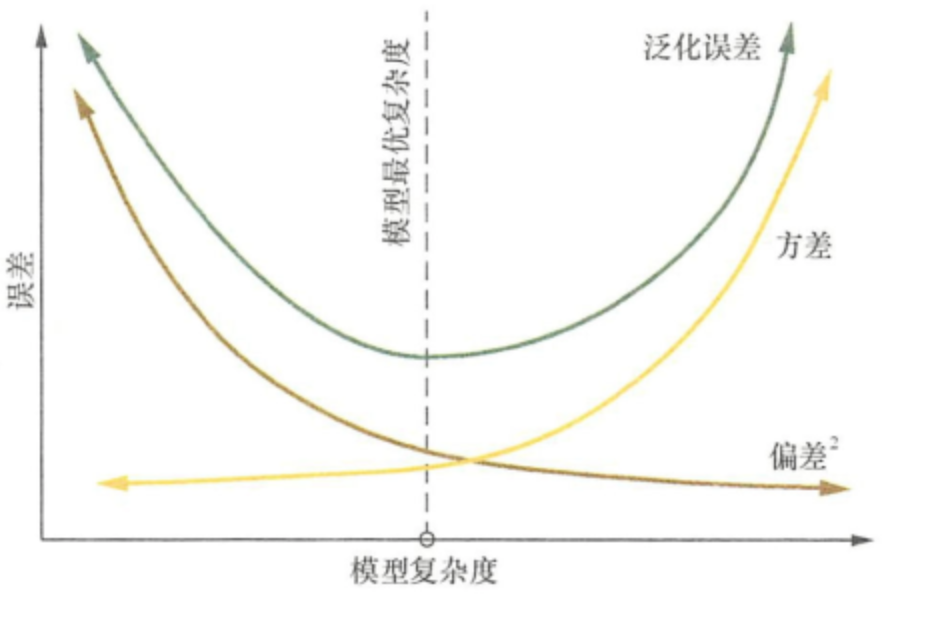
2. 什么是过拟合和欠拟合,为什么会出现这个现象
过拟合指的是在训练数据集上表现良好,而在未知数据上表现差。如图所示:
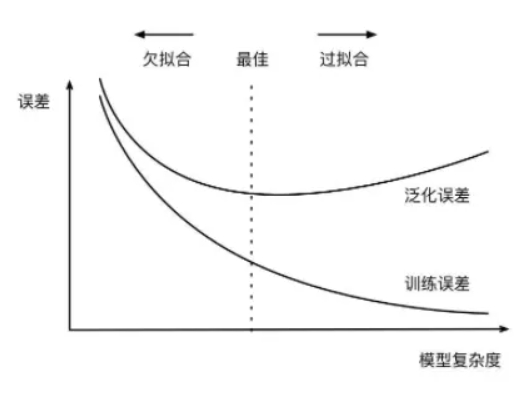
欠拟合指的是模型没有很好地学习到数据特征,不能够很好地拟合数据,在训练数据和未知数据上表现都很差。
过拟合的原因在于:
-
参数太多,模型复杂度过高;
-
建模样本选取有误,导致选取的样本数据不足以代表预定的分类规则;
-
样本噪音干扰过大,使得机器将部分噪音认为是特征从而扰乱了预设的分类规则;
-
假设的模型无法合理存在,或者说是假设成立的条件实际并不成立。
欠拟合的原因在于:
-
特征量过少;
-
模型复杂度过低。
3. 怎么解决欠拟合
-
增加新特征,可以考虑加入进特征组合、高次特征,来增大假设空间;
-
添加多项式特征,这个在机器学习算法里面用的很普遍,例如将线性模型通过添加二次项或者三次项使模型泛化能力更强;
-
减少正则化参数,正则化的目的是用来防止过拟合的,但是模型出现了欠拟合,则需要减少正则化参数;
-
使用非线性模型,比如核SVM 、决策树、深度学习等模型;
-
调整模型的容量(capacity),通俗地,模型的容量是指其拟合各种函数的能力;
-
容量低的模型可能很难拟合训练集。
4. 怎么解决过拟合(重点)
-
获取和使用更多的数据(数据集增强)——解决过拟合的根本性方法
-
特征降维:人工选择保留特征的方法对特征进行降维
-
加入正则化,控制模型的复杂度
-
Dropout
-
Early stopping
-
交叉验证
-
增加噪声
5. 为什么参数越小代表模型越简单?
因为参数的稀疏,在一定程度上实现了特征的选择。
越复杂的模型,越是会尝试对所有的样本进行拟合,甚至包括一些异常样本点,这就容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反映了在这个区间里的导数很大,而只有较大的参数值才能产生较大的导数。因此复杂的模型,其参数值会比较大。 因此参数越少代表模型越简单。
6. 为什么L1比L2更容易获得稀疏解?(重点)
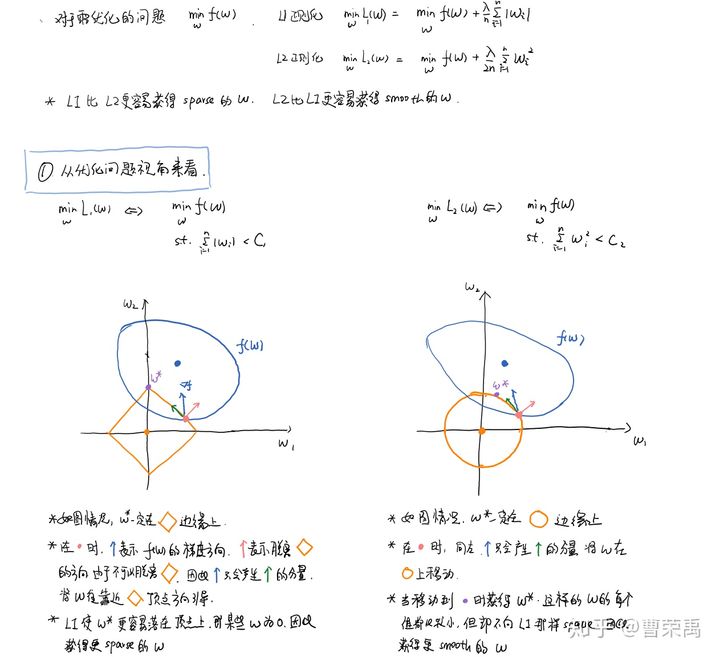

7. Dropout为什么有助于防止过拟合?(重点)
-
取平均的作用
先回到标准的模型即没有dropout,我们用相同的训练数据去训练5个不同的神经网络,一般会得到5个不同的结果,此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9,其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合,取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
-
减少神经元之间复杂的共适应关系
因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测,它不应该对一些特定的线索片段太过敏感,即使丢失特定的线索,它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1,L2正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
-
Dropout类似于性别在生物进化中的角色
物种为了生存往往会倾向于适应这种环境,环境突变则会导致物种难以做出及时反应,性别的出现可以繁衍出适应新环境的变种,有效的阻止过拟合,即避免环境改变时物种可能面临的灭绝。
参考链接:https://zhuanlan.zhihu.com/p/38200980
8. Dropout在训练和测试时都需要吗?
Dropout在训练时采用,是为了减少神经元对部分上层神经元的依赖,类似将多个不同网络结构的模型集成起来,减少过拟合的风险。而在测试时,应该用整个训练好的模型,因此不需要dropout。
9. Dropout如何平衡训练和测试时的差异呢?
Dropout 在训练时以一定的概率使神经元失活,实际上就是让对应神经元的输出为0。假设失活概率为 p ,就是这一层中的每个神经元都有p的概率失活。
例如在三层网络结构中,如果失活概率为0.5,则平均每一次训练有3个神经元失活,所以输出层每个神经元只有3个输入,而实际测试时是不会有dropout的,输出层每个神经元都有6个输入。
因此在训练时还要对第二层的输出数据除以(1-p)之后再传给输出层神经元,作为神经元失活的补偿,以使得在训练时和测试时每一层输入有大致相同的期望。
10. BN和Dropout共同使用时会出现的问题
BN和Dropout单独使用都能减少过拟合并加速训练速度,但如果一起使用的话并不会产生1+1>2的效果,相反可能会得到比单独使用更差的效果。
参考链接:https://www.zhihu.com/tardis/sogou/art/61725100
11. L1 和 L2 正则先验分别服从什么分布
先验就是优化的起跑线, 有先验的好处就是可以在较小的数据集中有良好的泛化性能,当然这是在先验分布是接近真实分布的情况下得到的了,从信息论的角度看,向系统加入了正确先验这个信息,肯定会提高系统的性能。
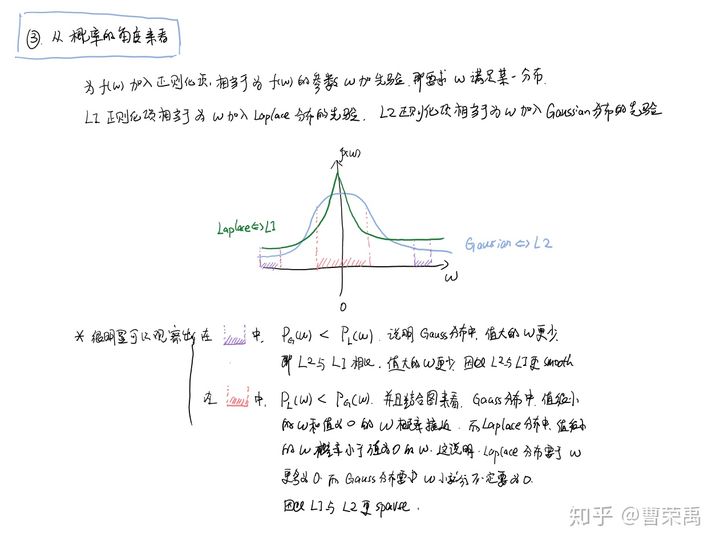
L1 正则先验分布是 Laplace 分布,L2 正则先验分布是 Gaussian 分布。
Laplace 分布公式为:
f ( x ) = 1 2 λ e − ∣ x − μ ∣ λ f(x)=\frac{1}{2 \lambda} e^{-\frac{|x-\mu|}{\lambda}} f(x)=2λ1e−λ∣x−μ∣
Gaussian 分布公式为:
f ( x ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) f(x)=2πσ1exp(−2σ2(x−μ)2)
对参数引入高斯正态先验分布相当于L2正则化:
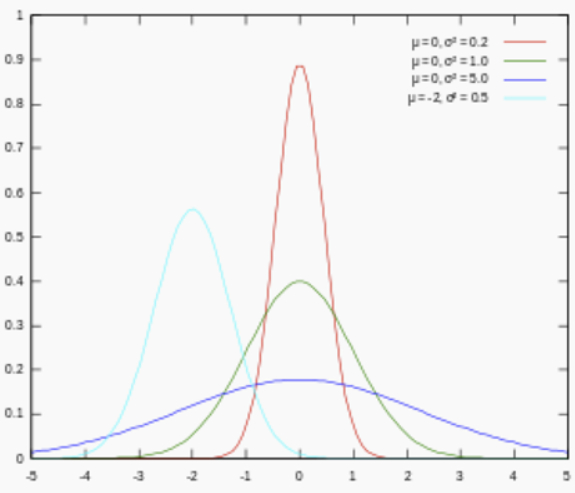
对参数引入拉普拉斯先验等价于 L1正则化:
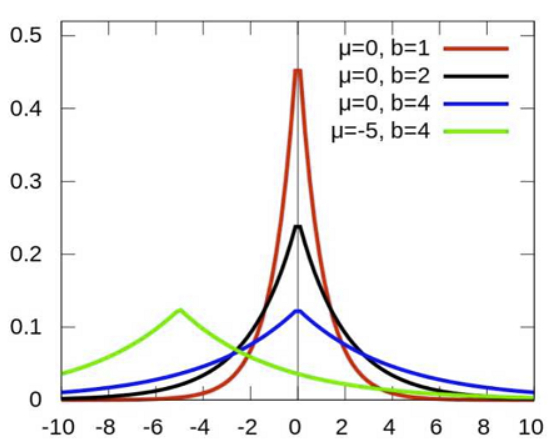
从上面两图可以看出, L2先验趋向零周围, L1先验趋向零本身。





:权限修饰符包Object类)


)






)



