供应链 | 顶刊OR论文精读：在线最小峰值作业调度的竞争算法

在这里插入图片描述

Competitive Algorithms for the Online Minimum Peak Job Scheduling

在这里插入图片描述
本文为OR期刊论文，原文信息：

Célia Escribe, Michael Hu, Retsef Levi (2023) Competitive Algorithms for the Online Minimum Peak Job Scheduling. Operations Research. Articles in Advance, pp. 1–16. https://doi.org/10.1287/opre.2021.0080

原文摘要总结如下：

本文探讨了一个基础的在线调度优化问题，即最小峰值作业调度（Minimum Peak Job Scheduling, MPJS）问题。该问题涉及一系列作业，每个作业均分配有特定的使用时段，针对某一稀缺而可循环利用的资源。本问题的核心目标是在一个调度间隔内，通过作业的实时安排，达到最小化峰值资源利用率（即，在整个调度间隔中最大化同时作业的数量）。

MPJS问题准确抓住了实践中实时预约调度场景的核心特征。

MPJS问题的离线模式，即所有作业均事先已知的情形，等同于众所周知的装箱问题，其中，作业对应于物品，单位资源对应于箱子。
MPJS问题的在线模式则提供了更高的调度灵活性，允许在最初仅确定调度时间的基础上，后续进行资源的动态分配，类似于装箱问题中跨容器移动物品的能力。

虽然已有广泛文献研究了在线装箱问题的各种变体模式，但现有文献尚未全面覆盖MPJS模型的特性。

本文首次介绍了一种适用于MPJS问题的竞争性在线算法——谐波重匹配（Harmonic Re-matching, HR）算法，并通过分析证明，该算法的渐进竞争比低于1.5。当前装箱问题的随机在线算法的最优下界为1.536，这一结果凸显了两种模型之间的基本差异。

关键词：装箱 • 在线算法 • 竞争分析

1. 问题背景

本文描述了一个基础的在线调度优化问题，即最小峰值作业调度（Minimum Peak Job Scheduling, MPJS）问题。该问题涉及一系列作业，每个作业均分配有特定的使用时段，针对某一稀缺而可循环利用的资源。本问题的核心目标是在一个调度间隔内，通过作业的实时安排，达到最小化峰值资源利用率（即，在整个调度间隔中最大化同时作业的数量）。

编者注：最小峰值作业调度（MPJS）问题是一个典型的优化问题，通常出现在运筹学、计算机科学和工业工程等领域。该问题的目标是在一定条件下安排一系列作业（或任务），以使得在任何给定时刻，执行中的作业数量的最大值（即峰值）最小化。这种类型的问题在实际应用中非常重要，比如在生产调度、计算资源分配、网络流量管理等方面都有广泛的应用。

MPJS问题的离线模式等同于装箱问题，但MPJS问题的在线模式则引入了不同的挑战，如资源分配的灵活性。与在线装箱问题相比，MPJS允许在调度完成后再分配资源，提供了更大的灵活性。例如，输液中心的病人预约调度反映了MPJS问题的实际应用。考虑一个有给定数量输液椅的输液中心。病人的预约请求在一天内随时间到达，每个预约请求到达时必须被安排到一个输液椅上，并指定预约的持续时间。该问题的目标是最小化输液椅的峰值数量，而峰值利用率通常决定了人员配备水平。其中，病人的预约对应于MPJS问题中的作业，输液椅对应于资源单位，预约持续时间对应于作业所需的预定时间。此外，一旦预约，预约的开始时间不能轻易改变，因为输液中心已经承诺了病人的特定时间，然而病人分配到的特定的输液椅可以在治疗当天确定。

本文开发了一种新的在线最小峰值作业调度（MPJS）算法，具有理论和实践上的良好性能。通过经典指标竞争比（Coffman等1996, 1999, 2013; Coffman和Csirik 2007）评估这些算法，也就是说，在线算法的性能是相对于一个离线最优算法来评估的，该算法在知道所有预约及其各自持续时间的情况下，做出最优的预约调度决策。

注：竞争比（Competitive Ratio）是在线算法分析中一个核心的概念，用来衡量在线算法性能的一个标准。在线算法指的是那些在没有完整信息的情况下逐步做出决策的算法，即算法必须在每一步骤中，仅根据到目前为止接收到的信息做出决策，而无法预见将来的事件或数据。竞争比是在线算法性能与最优离线算法性能之间的比值。最优离线算法假设有关未来事件的完全信息，因此可以做出最优的决策。竞争比越小，意味着在线算法的性能越接近最优解，算法越有效。

竞争比在多种计算问题中都有应用，包括但不限于：

缓存问题（如页面替换算法）
调度问题
路径规划
数据流处理

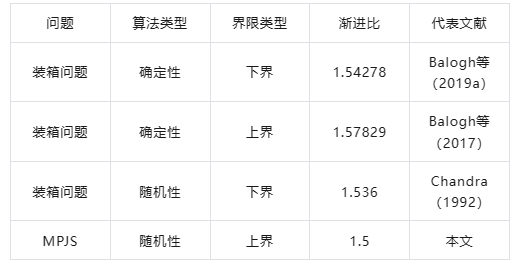
本文提出了谐波重匹配（Harmonic Re-matching, HR），该算法实现了1.5的渐进竞争比，优于装箱问题算法的理论上界1.536（Chandra 1992）。该算法利用MPJS问题的灵活性，通过特定作业类别的单边箱子的调度，优化了作业的"打包"过程。注：关于装箱算法性能的不同结果在下表1中进行了总结。

表1. 装箱问题和MPJS问题的比较

在这里插入图片描述

本文结构概述如下，供读者参考：

第2节：介绍并解释最小峰值作业调度（MPJS）问题，并推导出对MPJS问题的任何确定性在线算法的性能下界。
第3节：定义了提出的全新的谐波重匹配（HR）算法及其具体的匹配和重新匹配规则。
第4节：分析了HR算法的性能，展示了其渐进竞争比为1.5。

2. 模型描述

本节定义MPJS问题并描述模型符号。不失一般性地，假设给定的调度间隔长度为 $\leq 1$ 。

考虑有 $N$ 个作业依次到达，表示为 $A_1$ , …, $A_N$ ，预定时间为 $l_1$ , …, $l_N$ （满足 $\leq l_i \leq 1$ ）。这些作业需即时调度至资源池。设 $s_i$ 为作业 $A_i$ 的开始时间，满足 $\leq s_i$ 且 $s_i + l_i \leq 1$ 。对于调度问题 $A, l, s) = {(A_1, l_1, s_1), ..., (A_N, l_N, s_N)}$ ，时间 $t$ 的作业总数记为负载 $u_t = \sum_{i=1}^{N} {1}\{s_i \leq t < s_i + l_i\}$ 。调度问题的峰值负载（即最大箱子数）为 $\max_{0\leq t\leq 1} u_t$ 。问题目标是最小化结果调度的峰值负载。

在开始作业时间 $s_i$ 时，未来作业的信息未知。令 $A L G (I)$ 表示算法所需的最大箱子数， $OPT (I)$ 为最优离线算法所需最大箱子数。绝对竞争比定义为：
$\sup_{I \in \Sigma} \frac{ALG(I)}{OPT(I)}$
其中， $\Sigma$ 表示所有可能的作业序列空间。渐进竞争比则定义为：
$\lim_{N \to \infty} \sup_{I:OPT(I) \geq N} \frac{ALG(I)}{OPT(I)}$
命题 1: 对于任何可行调度 $(A, l, s)$ ，都可以找到一种将 $N$ 个作业分配至箱子的方式，恰用 $p ((A, l, s))$ 个箱子，每个作业由单个箱子处理。

命题1表明，最小化峰值负载的目标等同于最小化调度所有作业所需的最大箱子数量，以保证每个作业被单一箱子处理。将作业预定时间视为其“大小”（为便于与装箱问题比较，文中“预定时间”与“大小”术语将互换使用），该问题的离线模式即为众所周知的装箱问题，意味着任何在线装箱算法均可提供具有相同竞争比的解决方案。

针对此调度问题的任何在线确定性算法的绝对竞争比的下界。

命题 2: 对于MPJS问题的任何确定性在线算法，绝对竞争比 $\geq 1.5$ 。

3. 谐波重匹配算法(Harmonic Rematching Algorithm)

本节介绍谐波重匹配算法（HR算法），并展示其对调度问题具有1.5的渐进竞争比。

3.1 算法概述

HR算法基于两个核心思想：

作业分类：根据 $(\frac{1}{j+1}, \frac{1}{j}]$ 的调度需求将作业分为不同类别，借鉴了谐波装箱算法（Harmonic bin-packing algorithm, Lee and Lee 1985）和其他研究的分类方法。
作业分配：通过左侧和右侧单边箱子（left and right one-sided bins）的动态匹配与重新匹配来利用调度灵活性。左侧单边箱子（a left one-sided bin）从时间0开始到某个时间 $0 < s < 1$ 结束；右侧单边箱子（a right one-sided bin）从某个时间 $0 < s < 1$ 开始开始直至时间1结束。因此，开启一个左侧单边箱子对应于安排一个作业在时间 0 开始，同样，开启一个右侧单边箱子对应于安排一个作业在时间 1 结束。箱子的充满度（fullness）定义为该箱子中所有作业长度的总和。因为所有箱子的长度被标准化为一，箱子的充满度等同于其利用率。

上述两个核心思想使算法能在充满度（fullness）和重新匹配灵活性（rematching flexibility）之间平衡：旨在确保匹配的单边箱子充满度足够，同时保持足够的灵活性进行有效的重新匹配。当开启新的单边箱子时，算法随机选择是左侧还是右侧，以保持与单边箱子大小分布相关的特性，这在后续的竞争比分析中证明至关重要。

注：单边箱子是谐波重匹配算法中使用的一个概念，特指在调度问题中被设计来容纳同一类别中的作业的特定类型的箱子。这些箱子的特点是它们在调度过程中只被用来装载一侧（左侧或右侧）的作业，即要么从时间0开始直到某个特定时间点结束（左侧单边箱子），要么从某个特定时间点开始直到时间1结束（右侧单边箱子）。单边箱子的设计允许算法在分配作业到资源（箱子）时保持一定的灵活性，使得可以根据已调度的作业和未来可能到达的作业动态地进行匹配和重新匹配，以优化资源的利用率和减少所需的资源总量。

在HR算法中，单边箱子可以根据作业的大小进一步分类，如类型1、类型2细、和类型2胖单边箱子，每种类型针对不同大小范围的作业设计。这种分类方法和单边箱子的使用，帮助算法在满足作业的调度需求的同时，尽量减少峰值负载，即在任何给定时刻所需的最大资源数量。通过这种方法，HR算法旨在实现较低的渐进竞争比，即与最优离线算法相比，在线算法的性能度量。

3.2 创建单边箱子

3.2.1 作业分类

遵循先前研究，作业按大小划分为四类：非常大的作业（ $ℓ_i ∈ (\frac{2}{3}, 1]$ ），大作业（ $ℓ_i ∈ (\frac{1}{2}, \frac{2}{3}]$ ），中等作业（ $ℓ_i ∈ (\frac{1}{3}, \frac{1}{2}]$ ），小作业（ $ℓ_i ∈ (0, \frac{1}{3}]$ ）。小作业进一步细分为子类别 $I_j = (\frac{1}{j+1}, \frac{1}{j}]$ ，其中 $3 \leq j \leq 11$ 。

3.2.2 单边箱子类型

单边箱子仅包含同一类别的作业。对于非常大的作业、大作业和中等作业，单边箱子都由单个作业组成，分别称为非常大的单边箱子（very large one- sided bins）、大单边箱子（large one-sided bins）和中等单边箱子（medium one-sided bins）。
小作业箱子分为三种：类型1（Type 1 one-sided bins，充满度至1），类型2细（Type 2 thin one-sided bins，充满度至 $\frac{1}{3}$ ），类型2胖（Type 2 fat one-sided bins，充满度至 $\frac{1}{2}$ ）。

3.2.3 完整匹配单边箱子集合

随着作业的到达，算法通过创建单边箱子完整匹配单边箱子集合来组织作业。这些集合是特定类别的，即每个集合只包含来自一个类别的作业，仅定义于小和中等作业。类型2细单边箱子总能与对面的类型2胖单边箱子匹配，形成类型2箱子，如图1所示。

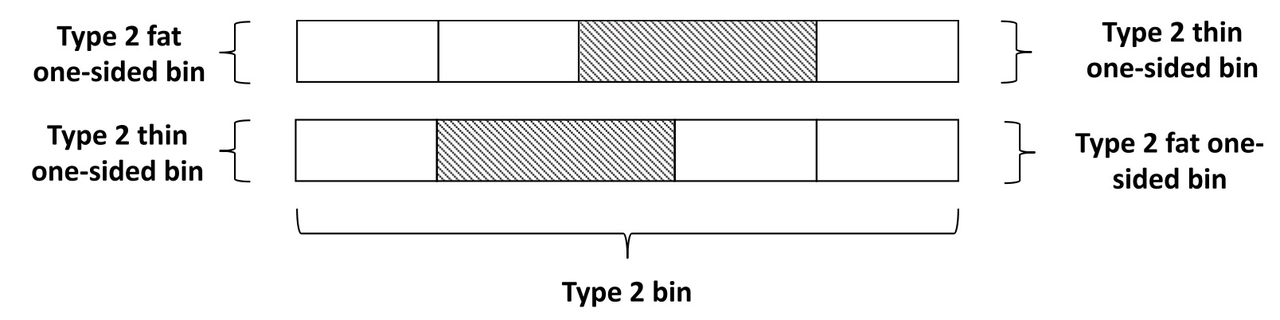
图1. 两种对称的类型2箱子

对于小作业（ $\frac{1}{3}$ ），通过结合类型1箱子和类型2箱子，可以创建一个完整的匹配单边箱子集合，其中类型2箱子通过暂时匹配类型2胖单边箱子与类型2细单边箱子得到。这样的匹配集合包含 $n_1$ 个类型1箱子和 $n_2$ 个类型2箱子， $n_2$ 为偶数。类型1箱子增加集合的充满度，而类型2箱子用以防备大作业的到来。
一个具有 $n_1$ 个类型1箱子和 $n_2$ 个类型2箱子的完整匹配集合具有以下特征：
- 按照类型2箱子的定义，存在 $n_2$ 个类型2细单边箱子和 $n_2$ 个类型2胖单边箱子。
- 每一侧（左侧和右侧）的类型2细单边箱子和类型2胖单边箱子数量相同。
- 注：完整匹配单边箱子集合的组成和类型1箱子与类型2箱子的比例，请读者自行参阅原文附录EC.4。每个作业类别的完整匹配集合至少为 $\frac{2}{3}$ 满。
对于中等作业，完整匹配集合仅由两个相对的中等单边箱子组成。如果单边箱子未按类别和类型指定的数量填满，则视为不完整；否则，视为完整。未满足形成其类别完整匹配集合所有标准的单边箱子组，视为不完整；否则，视为完整。

3.2.4 新作业到来

当新作业到达时，HR算法根据作业大小和当前单边箱子的状态决定如何调度：

非常大或大作业：创建新的单边箱子。如果一侧的同类单边箱子数量少，新箱子将在该侧创建；否则，以0.5概率随机选择左或右侧。这保持了大单边箱子数量的平衡。
中等作业：也用于创建新的单边箱子，遵循与大作业相同的侧面选择规则。如果一侧已有未匹配的中等作业，新作业将与其在对侧匹配，形成完整的匹配中等单边箱子。
小作业：首先尝试添加到同类别的不完整单边箱子中。若无不完整单边箱子但存在不完整匹配集合，则新作业用于开启新单边箱子并加入该集合；若无不完整集合，则创建新的匹配集合。新箱子类型的选择不影响分析结果。

这些规则确保大和中等单边箱子两侧数量大致平衡，最多相差一个作业。对于每个作业类别，一次最多只能有一个不完整的匹配单边箱子集合。

3.3 创建调度

本节概述了如何将完整匹配单边箱子集合转换为具体调度。目标是通过重新匹配来优化调度，特别是针对大单边箱子，以形成完全调度的箱子集合。

3.3.1 小作业箱子的重新匹配

类型2胖单边箱子总能相互匹配，因为它们的预定时间小于 $\frac{1}{2}$ 。
类型2细单边箱子能与大单边箱子匹配，因为它们的预定时间小于 $\frac{1}{3}$ 和 $\frac{2}{3}$ 。
当两个类型2箱子的细单边箱子位于相对两侧时，这两个箱子视为对称。
重新匹配过程中，使用两个对称的类型2箱子和两侧的大单边箱子。类型2细单边箱子重新匹配到对侧的大单边箱子，而类型2胖单边箱子相互重新匹配，只有在选择的类型2箱子对称时才可行。
为了重新匹配含有 $n_2$ 个类型2箱子的集合，需在每侧选择 $\frac{n_2}{2}$ 个大单边箱子。
成功的重新匹配减少了总箱子数量，形成重新匹配的箱子集合。\

图2展示了从初始完整匹配集合到重新匹配集合的转换示例，其中包括选择的大单边箱子和最终的重新匹配的箱子集合。

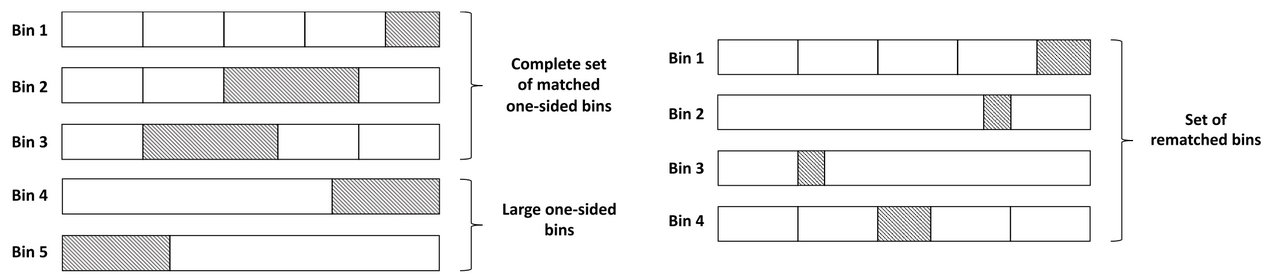
图2. 单边箱子的重新匹配过程

3.3.2 将额外的大作业分配给小作业

小作业的重新匹配箱子集合会涵盖一定比例的大作业。此过程旨在通过向集合中添加额外的大单边箱子，提高包含大作业的箱子比例，直至超过 $\frac{2}{3}$ 。如果重新匹配的箱子集合中含有大作业的比例已满足这一条件，则不需额外分配大作业。这一分配过程确保额外的大单边箱子被纳入到重新匹配的箱子集合中，以达到或超过大作业的目标比例。

3.3.3 小作业的完全调度箱子集合

小作业的完全调度箱子集合是通过以下步骤创建的：

重新匹配过程：首先，按照3.3.1节的描述，对完整匹配单边箱子集合执行重新匹配过程，得到一组重新匹配的箱子集合。
分配额外大作业：接着，如3.3.2节所述，将额外的大作业分配至重新匹配的箱子集合，直至达到完全调度的状态，即大作业箱子比例超过 $\frac{2}{3}$ 。

如果任一步骤无法完全实施，则称为部分调度的箱子集合。在整个调度过程中，首先将大作业按大小递减顺序分别在左侧和右侧排列，用于重新匹配和分配。通过迭代选择小作业的完整匹配单边箱子集合，形成完全调度的箱子集合。完成这些步骤后，未参与重新匹配或未被分配到任何完整集合的大单边箱子被称为未分配的大单边箱子。

3.3.4 中等箱子的重新匹配

创建小作业的完全调度箱子集合过程终止于以下情形之一：未分配的大作业耗尽；或所有重新匹配的小箱子已分配大作业，达到或超过 $\frac{2}{3}$ 的大作业比例。此时，可能留有部分调度的小作业箱子集合。未分配的大作业和匹配的单边中等作业箱子，则进入中等作业箱子的重新匹配过程。

在重新匹配中等作业箱子时：

未分配的大单边箱子和中等单边箱子按大小递增顺序排列于各自一侧。
大作业与相同排名的中等作业匹配，形成单个箱子（包含一个大作业和一个中等作业），条件是它们的总大小不超过1。
创建一系列单个箱子，每个箱子包含一个大作业和一个中等作业，形式为(L, M)或(M, L)。这些箱子也构成完全调度的中等箱子集合，因为集合中含有大作业的箱子比例大于 $\frac{2}{3}$ 。

在中等作业的重新匹配过程中，可能因为(L, M)与(M, L)匹配的数量不同，留下未分配的大作业和单边中等箱子。这种情况下，继续将未分配的大作业与中等箱子配对，每个配对分配两个大作业，形成完全调度的中等箱子集合，直到所有可能的配对完成。这一步骤确保了小作业和中等作业的有效调度，最大化了箱子集合中大作业的比例，同时保持了调度的灵活性和效率。

4. 在线调度算法的竞争分析

4.1. 概述

在线调度算法的竞争分析目标是证明HR算法的渐进竞争比为1.5，即当作业数量无限增加时，算法的性能接近最优离线算法的1.5倍。分析步骤概述如下：

基本属性：首先证明所有完全调度的箱子集合的充满度至少为 $\frac{2}{3}$ ，并且含有大作业的箱子比例不低于 $\frac{2}{3}$ 。
作业大小分布属性：展示大作业和中等作业在每侧的大小分布特性。
不同情景分析：考虑3种调度情境，使用箱子的充满度和大作业比例两个下界来推导前两种情景的渐进竞争比。若所有箱子至少 $\frac{2}{3}$ 满，或含有大作业的箱子比例至少为 $\frac{2}{3}$ ，由于每个箱子最多只能装一个大作业，OPT至少需要使用HR算法使用量的 $\frac{2}{3}$ 来容纳所有作业，直接导出1.5的渐进竞争比。最后，通过考察大作业和中等作业的大小分布来推导渐进比率。

4.2 完全调度箱子集合的属性

引理1至6展示了完全调度箱子集合的两个关键属性：充满度和大作业比例。

引理 1: 每个作业类别的完整匹配单边箱子集合的平均充满度至少为 $\frac{2}{3}$ 。
引理 2: 对于包含 $n_1$ 个类型1箱子和 $n_2$ 个类型2箱子的完整匹配单边箱子集合，在执行 $k$ 次部分重新匹配过程（ $\leq \frac{n_2}{2}$ ）后，新箱子集合的平均充满度仍大于或等于 $\frac{2}{3}$ 。
引理 3: 每个作业类别的重新匹配箱子集合的平均充满度大于或等于 $\frac{2}{3}$ 。
引理 4 & 5: ## 标题展示了如何通过将额外的大单边箱子分配给重新匹配的箱子集合，达到大作业箱子比例大于或等于 $\frac{2}{3}$ ，同时保持箱子集合的平均充满度大于 $\frac{2}{3}$ 。
引理 6: 一组完全调度的箱子的平均充满度至少为 $\frac{2}{3}$ ，且含有大作业的箱子比例大于或等于 $\frac{2}{3}$ 。这基于引理4和引理5的结果，证明了额外的大作业可以被有效地分配给重新匹配的箱子集合，保持充满度和大作业比例的目标。

这些引理共同证明了HR算法在调度过程中成功维持了关键的箱子集合属性，即充满度和大作业比例，为实现1.5的渐进竞争比提供了基础。

4.3 大作业和中等作业的有界渐进不平衡

本节探讨了大作业和中等作业的不平衡问题，特别是当作业数量无限时。尽管算法能在每次迭代中保持左右大作业数量的近似平衡，但按大小递增顺序排列时，这种平衡并不总能保证。

不平衡定义: 考虑一个按大小递增顺序的无限大作业序列， $Y_k=1$ 表示第 $k$ 个较小的作业放置在左侧的事件， $Y_k=-1$ 表示它放置在右侧的事件。不平衡度 $I_L$ 是指在左侧和右侧大作业数量差异的度量，计算为 $L$ 个顺序大作业的左右放置差异之和，即 $I_L = \sum_{k=1}^{L} Y_k$ 。 $I_L > 0$ 意味着左侧的大作业较多，而 $I_L < 0$ 则表示右侧的较多。

引理 7：考虑一个按大小递增顺序的无限大作业序列，记作 $k = 1, ..., L$ 。令 $a_1, ..., a_L)$ 表示 $L$ 个最小大作业的相应到达时间，其中 $\leq a_k \leq L$ ，并且 $Y_1, ..., Y_L)$ 是它们到达时匹配的相应边，具体地，如果第 $k$ 个最小的大型作业放置在左侧，则 $Y_k=1$ ，如果它放置在右侧，则 $Y_k=-1$ 。那么可以得到：
$\limsup_{L \to \infty} \frac{\pm I_L}{L} = 0 \quad \text{a.s.}$

4.4 渐进竞争比为1.5

4.4.1 符号

符号定义：

$v$ ：非常大作业的单边箱子数量。
$z$ ：完全调度箱子集合中的箱子数量。
$n$ ：小作业部分调度箱子集合中的箱子数量。
$m$ ：中等作业部分调度箱子集合中的箱子数量。
$\ell$ ：未分配的大单边箱子数量。
$k$ ：不完整匹配单边箱子集合中的箱子数量，由常数 $K$ 上界。

4.4.2 情景1：没有未分配的大单边箱子

可能是由小作业的部分调度箱子集合（ $\ell = 0$ 和 $n > 0$ ）或由中等作业的部分调度箱子集合且没有未分配大单边箱子（ $n = 0$ ， $\ell = 0$ ， $m > 0$ ）导致。

引理 8: 如果没有未分配的大单边箱子（ $\ell = 0$ ），则算法 ALG 的性能不会超过最优解 OPT 的1.5倍加上一个与 OPT 无关的常数 K。

证明概要: 没有未分配的大单边箱子意味着所有这些箱子都已在重新匹配过程和分配过程中被使用。根据引理 6，所有完全调度的箱子集合的平均充满度超过 $\frac{2}{3}$ ，从而所有箱子平均至少 $\frac{2}{3}$ 满。引理 1 显示所有完整匹配的单边箱子集合平均至少 $\frac{2}{3}$ 满。引理 2 和 3 表明，所有部分调度箱子集合的平均充满度也超过 $\frac{2}{3}$ ，意味着所有箱子平均至少 $\frac{2}{3}$ 满。最终，所有非常大的作业至少 $\frac{2}{3}$ 满，所有中等作业至少 $\frac{1}{3}$ 满。这表明 OPT 至少需要 ALG 中 $\frac{2}{3}$ 数量的箱子来容纳所有作业，因此 $\leq \frac{3}{2} OPT + K$ 。

4.4.3 情景2：存在未分配的大单边箱子和完全调度的箱子集合

此情景下有未分配的大单边箱子（ $\ell > 0$ ）而没有部分调度的小或中等作业箱子集合（ $n = 0$ 和 $m = 0$ ）。

引理 9: 如果存在未分配的大单边箱子且只有完全调度的箱子集合（ $n = 0$ ， $m = 0$ ，且 $\ell>0$ ），则 ALG 的性能不会超过 OPT 的1.5倍加上一个与 OPT 无关的常数 K。

证明概要: 根据引理 6，完全调度的箱子集合中含有大作业的箱子比例大于等于 $\frac{2}{3}$ 。因此，这些箱子至少包含 $\frac{2}{3}$ 数量的大作业。假设中没有部分调度的箱子集合，意味着 OPT 至少等于 $\frac{2}{3}z + \ell$ ，因为 OPT 每个箱子最多不能装超过一个大作业。同时，ALG 为 $\ell + k$ 且 $\leq K$ 。这表明 $\leq \frac{3}{2} OPT + K$ 。

4.4.4. 情景3：未分配的大单边箱子和部分完成的中等作业调度箱子集合

存在未分配的大单边箱子和部分调度的中等箱子集合（ $\ell > 0$ 和 $m > 0$ ），这可能导致很多大单边箱子未被分配且中等箱子集合的大作业比例不足 $\frac{2}{3}$ 。

引理 10: 考虑一个无限序列的项目，其中存在未分配的大单边箱子和部分预定的中等作业箱子集合（即， $\ell > 0$ 和 $m > 0$ ）。那么，
$\lim_{N \to \infty} \sup_{I:\text{OPT}(I) \geq N} \frac{\text{ALG}(I)}{\text{OPT}(I)} \leq \frac{3}{2}$
这意味着，在存在无限数量的大和中等作业时，即使有未分配的大箱子和部分完成的中等作业箱子集合，算法（ALG）与最优解（OPT）的渐进竞争比仍然不超过1.5。这个结果证明了即使在面对复杂情况时，算法的性能也几乎肯定地非常接近最优性能。

综上，可以得出如下定理。

定理 1. 考虑一个无限序列的项目。HR算法几乎必然地具有3/2的渐进竞争比：
$\lim_{N \to \infty} \sup_{I:\text{OPT}(I) \geq N} \frac{\text{ALG}(I)}{\text{OPT}(I)} \leq \frac{3}{2}$
定理 1 的证明概要：这无限的项目序列将对应于先前指定的三种情景中的一个，因为它们涵盖了所有可能的情形。利用引理8到10，我们可以直接得出，几乎必然地，当N趋向于无穷大时， $A L G (I)$ 与 $OPT (I)$ 的比值的上确界小于或等于1.5。

在此基础上，作者设计了计算实验，HR算法通过对随机生成的预约请求序列进行评估，其性能结果与计算出的最优离线目标值进行了对比。实验涉及不同规模的预约数（n值），每种规模下随机生成1000个独立的序列，每个序列包含n个预约，每个预约持续时间也随机生成，采用了不同的概率分布模型来生成这些持续时间。实验结果显示，在离散均匀分布下，HR算法通常能达到接近最优的性能。但当预约作业的大小集中在较小的区间内时，算法的性能有所下降。通过适当地根据作业长度分布调整HR算法，可以在实际应用中获得更优的竞争比。实验中得到的竞争比远优于理论上的渐近保证1.5。此外，随着预约数量的增加，算法的平均性能比也呈现下降趋势。

5. 结论

本文介绍并研究了一个称为在线最小峰值作业调度（MPJS）问题的基础在线作业调度模型，并发现其离线版本与经典的装箱问题相似，但在线版本由于其额外的灵活性而有所不同。文中提出的在线谐波重匹配算法成功实现了比已知随机在线装箱算法更好的1.5渐进竞争比。算法在各种计算实验中展现了出色的实证性能，表明其在现实世界调度问题中具有应用价值。尽管如此，关于MPJS问题的渐进上界是否最优，以及问题的可能扩展，例如引入特定的调度约束，仍是值得进一步探究的开放性问题。

参考文献

Coffman EG, Csirik J (2007) Performance guarantees for one- dimensional bin packing. Gonzalez TF, ed. Handbook of Approxi- mation Algorithms and Metaheuristics (CRC Press, Boca Raton, FL), 33–59.
Coffman EG, Garey MR, Johnson DS (1996) Approximation algori- thms for bin packing: A survey. Hochbaum DS, ed. Approximation Algorithms for NP-Hard Problems (PWS Publishing Company, Boston), 46–93.
Coffman EG, Galambos G, Martello S, Vigo D (1999) Bin packing approximation algorithms: Combinatorial analysis. Du DZ, Par- dalos PM, eds. Handbook of Combinatorial Optimization (Springer, Boston), 151–207.
Coffman EG, Csirik J, Galambos G, Martello S, Vigo D (2013) Bin packing approximation algorithms: Survey and classification. Pardalos PM, Du D-Z, Graham RL, eds. Handbook of Combinato- rial Optimization (Springer, New York), 455–531.
Balogh J, Be ́ ke ́ si J, Do ́ sa G, Epstein L, Levin A (2017) A new and improved algorithm for online bin packing. Preprint, submitted July 6, https://arxiv.org/abs/1707.01728.
Balogh J, Be ́ ke ́ si J, Do ́ sa G, Epstein L, Levin A (2019a) A new lower bound for classic online bin packing. Internat. Workshop Approximation Online Algorithms (Springer), 2047–2062.
Chandra B (1992) Does randomization help in online bin packing? Inform. Processing Lett. 43:15–19.
Lee CC, Lee DT (1985) A simple on-line bin-packing algorithm. J. ACM 32(3):562–572.