激活函数选得好，模型性能差不了！17个方法，让网络训练更高效

激活函数是神经网络中不可或缺的组成部分，它们通过引入非线性特性，增强了网络的表达能力和学习能力。常用的激活函数主要可以分为两大类：饱和激活函数、非饱和激活函数。其中sigmoid和tanh是饱和激活函数，而ReLU及其变体则是非饱和激活函数。

在神经网络的不断发展中，我们一直在探索更有效的激活函数，以提升网络的性能和适应性。这其中具有代表性的成果就有Swish和Mish。

Swish激活函数：一种非线性激活函数，结合了输入值和sigmoid变换，用于深度学习模型中增强模型的表征能力。
Mish激活函数：受Swish启发的一种更平滑的激活函数，在图像识别和泛化性能上展现出了卓越的表现。

本文整理了深度学习6个常用的激活函数以及2个新兴的激活函数，每种激活函数都附上了最新的研究成果（共17篇），方便各位学习。

论文和代码需要的同学看文末

新兴激活函数

Swish:

Swish是通过机器学习技术发现的一种新型激活函数，它在处理负输入时表现出了比ReLU更好的性能。

数学形式：

适用场景：

卷积神经网络（CNN）：在处理图像识别和分类任务时，Swish可以提高模型的精度。
循环神经网络（RNN）：在处理序列数据，如时间序列预测或自然语言处理任务时，Swish可以帮助模型捕捉长期依赖关系。
Transformer模型：在自然语言处理领域，尤其是在处理注意力机制时，Swish可以作为激活函数来提高模型的性能。

源文：SWISH: A SELF-GATED ACTIVATION FUNCTION

方法论/创新点：

Swish是一种简单的非单调平滑函数，定义为f(x) = x · sigmoid(x)，其中sigmoid(x) = (1 + exp(−x))−1。
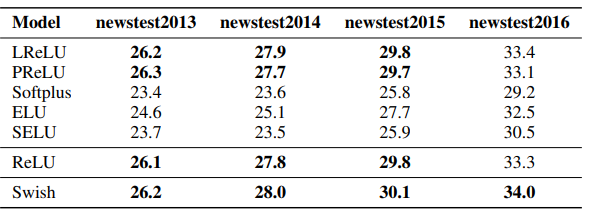
通过在多个挑战性数据集上进行的实验，论文展示了Swish在深层网络中往往比ReLU表现得更好。
易于实现和替换：Swish的简单性和与ReLU的相似性使得实践者可以轻松地在任何神经网络中用Swish单元替换ReLU。

Mish：

由Swish的自门控属性启发而来，提供了一种自我调节的平滑、连续且非单调的激活方式，旨在提高神经网络的准确性和泛化能力。

数学形式：

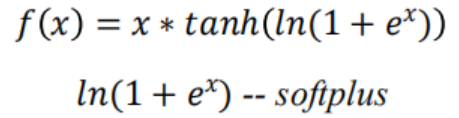
适用场景：

图像识别任务：Mish在处理图像识别任务时表现良好，因为它能够提供更平滑的梯度，有助于模型学习更复杂的特征。
泛化能力强：Mish的设计考虑了理想激活函数的特性，如平滑性和处理负号的能力，这使得它在各种数据集上都有很好的泛化能力。
神经网络架构：Mish可以用于各种神经网络架构中，包括但不限于卷积神经网络（CNN）和循环神经网络（RNN）。

源文：Mish: A Self Regularized Non-Monotonic Activation Function

方法论/创新点：

提出新型激活函数：定义了Mish激活函数，具有自正则化、非单调的特性。
性能提升：在图像分类和对象检测任务中，Mish相比其他激活函数显示出更好的性能。
数学特性分析：探讨了Mish与Swish函数家族的关系，并分析了其导数行为。
计算效率优化：开发了Mish-CUDA版本，提高了激活函数在实际应用中的计算效率。

非饱和激活函数

ReLU:

这是深度学习中最常用的激活函数之一，在输入值大于0时导数为1，小于0时导数为0，让网络能够有效地学习复杂的模式。

数学形式：

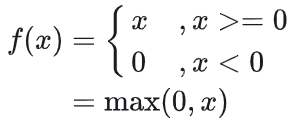
适用场景：

多层感知机（MLPs）：ReLU可以用于多层感知机网络中的隐藏层。它提供了非线性特性，使得MLP能够捕捉复杂的数据模式。
卷积神经网络（CNNs）：在卷积神经网络中，ReLU通常被用作卷积层之后的激活函数。它帮助网络学习图像、视频等数据的局部特征表示。
深度神经网络：ReLU激活函数有助于解决深度神经网络中的梯度消失问题，因为它的梯度在正值区间内是常数1，这有助于深层网络中梯度的有效传播。

例文：Exact Verification of ReLU Neural Control Barrier Functions

方法论/创新点：

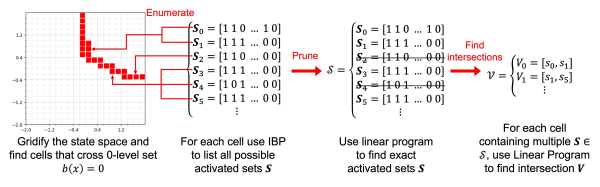
提出了一种新的算法来验证具有ReLU激活函数的神经网络控制障碍函数（NCBFs）的安全性，解决了传统方法无法处理的非可微分问题。
基于Nagumo定理的推广，提出了验证NCBFs安全性的精确条件。
设计了一种算法，通过分解NCBF并结合区间传播和线性松弛技术来降低计算复杂性。
验证方法不依赖于特定的控制策略，提高了设计的灵活性和可调性。

Leaky ReLU:

Leaky ReLU是ReLU的一个变种，解决了ReLU在输入小于0时导数为零的问题。

数学形式：

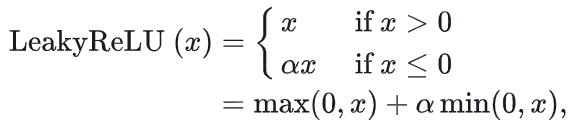
适用场景：

避免“死亡ReLU”问题：使用Leaky ReLU可以确保即使神经元接收到负输入，它们仍然能够学习并更新权重。
提高模型稳定性：Leaky ReLU提供了比标准ReLU更稳定的梯度，让模型能够更平稳地收敛。
处理稀疏数据：Leaky ReLU可以激活重要的神经元并抑制不重要的神经元，从而提高网络的泛化能力。

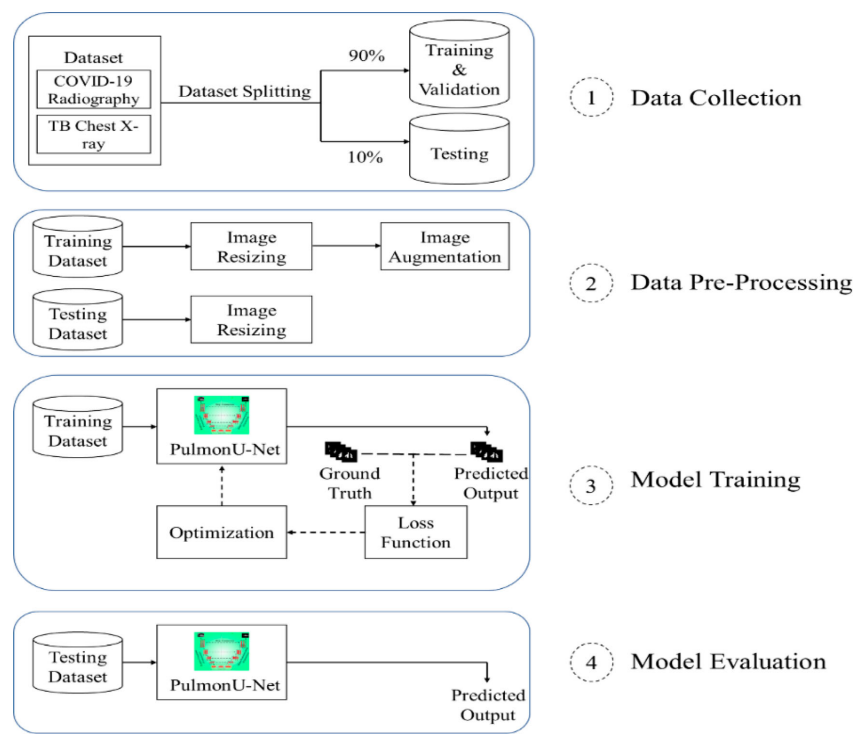
例文：PulmonU-Net: a semantic lung disease segmentation model leveraging the benefit of multiscale feature concatenation and leaky ReLU

方法论/创新点：

PulmonNet模块：这是一个创新的肺部疾病语义分割模型，利用不同尺寸的滤波器来处理多尺度的X射线特征，提高了对感染区域的识别能力。
多尺度特征融合：通过在编码器的深层中添加PulmonNet模块，模型能够有效地结合全局和局部特征，解决了消失梯度和过拟合问题。
Leaky ReLU激活函数：使用Leaky ReLU激活函数确保在学习过程中神经元的持续活动，从而提高了模型的稳定性和性能。
高准确度：模型在Dice相似性系数（DSC）上达到了94.25%，在IoU（交并比）上达到了88.3%，显示出其在肺部疾病分割任务中的高精度。

PReLU:

PReLU是Leaky ReLU的参数化版本，它允许学习alpha参数，而不是使用预设的值。

数学形式：

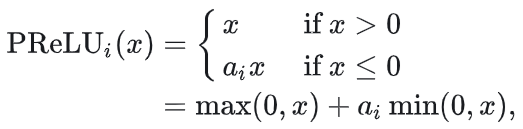
适用场景：

图像识别：PReLU已被证明在处理图像识别任务时，如ImageNet-2012分类数据集上，能够有效降低top-5错误率。这表明PReLU可以提升视觉识别系统的性能。
深度学习网络：PReLU引入了可学习的参数来优化模型的非线性特性，特别适用于深度神经网络。
过拟合控制：PReLU通过提供负数区间的线性响应，让模型学习更复杂的数据表示，从而在一定程度上减少过拟合现象。

源文：Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification

方法论/创新点：

参数化修正线性单元（PReLU）：提出了一种新的激活函数PReLU，它是传统ReLU的泛化形式。PReLU通过自适应学习激活函数的参数，提高了模型的拟合能力，同时几乎不增加额外的计算成本，并且只带来很少的过拟合风险。
针对深度修正模型的初始化方法：论文提出了一种新的初始化方法，特别针对修正激活函数（如ReLU/PReLU）的非线性特性，使得可以直接从零开始训练极深的修正模型，探索更深层次或更宽的网络架构。

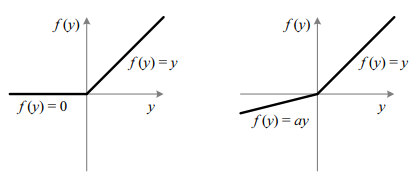
ELU:

ELU函数结合了Sigmoid和Leaky ReLU的特点，在负数区域的导数接近于零，有助于缓解梯度消失问题。

数学形式：

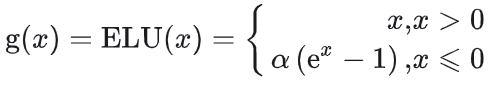
适用场景：

加速训练过程：与ReLU相比，ELU可以提供更快的训练时间。因为ELU对于所有负值的梯度都是非零的，有助于网络在训练过程中更快地传播和更新梯度。
避免神经元死亡：ELU没有所谓的“死亡神经元”问题，即在训练过程中某些神经元变得不活跃，不再更新权重的情况。这是因为ELU在输入为负值时仍然有非零梯度。
减少偏置偏移：ELU通过减少偏置偏移的影响，使得网络的梯度更加接近于单位自然梯度，这有助于网络的稳定性和收敛性。

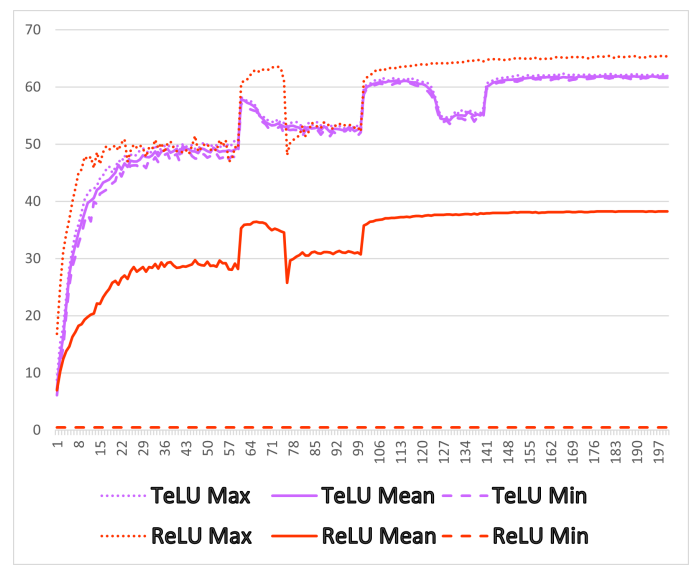
例文：STABLE AND ROBUST DEEP LEARNING BY HYPERBOLIC TANGENT EXPONENTIAL LINEAR UNIT (TELU)

方法论/创新点：

提出新的激活函数TeLU：引入了超双曲正切指数线性单元（TeLU），这是一种新型的激活函数，旨在解决现有激活函数（如ReLU、GELU等）的梯度消失和爆炸问题。
理论优势：TeLU的设计基于其在Fisher信息矩阵方面的理论优势，有助于形成更平滑的优化景观，从而提高训练的稳定性和收敛速度。
鲁棒性和稳定性：TeLU显示出对小噪声和扰动的高鲁棒性，以及在各种实验条件下的稳定性，这使其成为深度学习应用中潜在的新标准激活函数。
全局收敛性：论文还证明了在满足特定条件下，使用TeLU的神经网络能够全局收敛到最优解。

饱和激活函数

Sigmoid:

Sigmoid函数将输入映射到0和1之间，常用于二分类问题的输出层，缺点是容易产生梯度消失问题。

数学形式：

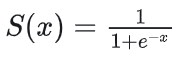
适用场景

逻辑回归模型：在二分类问题中，Sigmoid函数常用于模型的输出层，因为它可以将输出值映射到0和1之间，这可以解释为样本属于某个类别的概率。
神经网络隐藏层：Sigmoid函数也可用于神经网络的隐藏层，其平滑性和可微性有助于解决梯度消失问题，使得网络训练更加稳定。
边缘检测算法：在图像处理中，Sigmoid函数能将像素值映射到0和1之间，用以表示边缘的强度。

例文：Enhancing Convolutional Neural Network Performance through Optimized Sigmoid Activation Function Modeling

方法论/创新点：

优化Sigmoid激活函数：通过调整Sigmoid函数中的系数和常数，提出了一种改进的Sigmoid激活函数，以提高卷积神经网络（CNN）的性能。
参数调优：研究了在有限硬件条件下，通过微调CNN中Sigmoid激活函数的参数（包括α、β、γ、ε和δ）来提高准确性和计算效率。
性能提升：实验结果显示，通过优化Sigmoid函数的参数，可以在保持计算时间高效的同时，显著提高模型的准确性。

Tanh:

Tanh函数将输入映射到-1和1之间。与Sigmoid相比，Tanh的中心点在零点，因此在某些情况下效果更好。

数学形式：

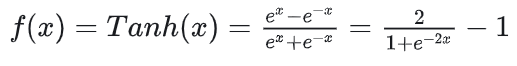
适用场景：

神经网络的隐藏层：由于tanh函数的输出范围是(-1, 1)，它是以0为中心的，这意味着它可以帮助模型学习到输入数据的对称性。
LSTM单元：在长短期记忆（LSTM）网络中，tanh函数通常用于控制信息的流向。它可以将细胞状态压缩到-1和1之间，这有助于保持网络的稳定性并防止梯度爆炸或消失。
特征缩放：在某些情况下，tanh函数可以用于特征缩放，将特征值缩放到一个固定的范围内，这有助于提高模型的训练效率和性能。

例文：Tanh Works Better With Asymmetry

方法论/创新点：

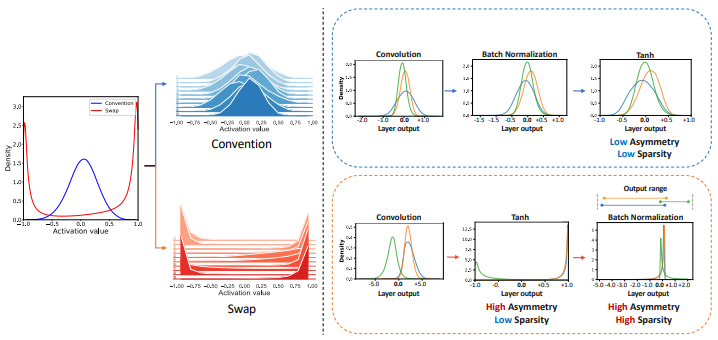
顺序交换现象：发现在使用Tanh等有界激活函数时，将批量归一化（Batch Normalization, BN）置于激活函数之后（Swap顺序）相比于传统的BN在激活函数之前（Convention顺序）能够显著提升模型性能。
不对称饱和分析：通过观察单个激活函数的输出分布，发现许多通道呈现出不对称饱和现象，这与整体层的对称分布不同。
性能提升机制：提出不对称饱和有助于提升模型性能的假设，并通过实验验证了这一假设。BN在有界激活函数之后能够将激活函数的输出重新定位到接近零的位置，从而增加了模型的稀疏性，进一步提升了性能。
移位Tanh函数：基于这些发现，提出了一种移位Tanh函数，通过引入不对称性来强制产生稀疏输出，实验结果显示这种移位Tanh函数在多种架构和数据集上都取得了更高的准确率。