avier初始化方法是一种常用的神经网络参数初始化方法，旨在有效地初始化权重，以促进神经网络的训练。该方法的提出者是Xavier Glorot和Yoshua Bengio，因此得名为“Xavier”。

在深度学习中，参数初始化是至关重要的，因为它直接影响着网络的收敛速度和性能。不恰当的初始化可能会导致梯度消失或梯度爆炸等问题，从而影响模型的训练效果。

Xavier初始化方法的主要思想是根据网络层的输入和输出的数量来确定权重的初始值，以保持信号在前向传播和反向传播过程中的稳定性。具体来说，对于一个具有n个输入和m个输出的全连接层（或卷积核），Xavier初始化将权重初始化为均值为0、方差为 2 / (n + m) 的高斯分布，或者在均匀分布中采样。公式表达为：

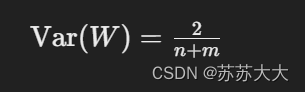
其中，\text{Var}(W)Var(W) 是权重的方差，nn 是输入数量，mm 是输出数量。

Xavier初始化的优点在于，它能够在避免梯度消失或梯度爆炸的同时，使得每一层的激活值保持在一个较合适的范围内，有利于提高模型的训练效率和性能。然而，对于某些特定的网络结构或激活函数，Xavier初始化可能并不是最佳选择，因此在实践中可能需要根据具体情况进行调整或改进。

总之，Xavier初始化方法为深度学习模型的参数初始化提供了一种简单而有效的策略，是目前广泛应用于各种神经网络架构中的一种常用方法。