海洋资料的获取与分析
相关数据代码等资料已上传入群中
海洋资料下载和介绍
AO和NAO指数均取自美国气候预测中心(Climate Prediction Center, CPC)发布的月平均指数,时间跨度为1950-2022年。由于AO和NAO在冬季最强,因此本文选取1950/1951-2021/2022年12月至次年2月作为冬季指数以及12月至次年2月平均值作为冬季平均来分别考察其周期变化。AO模态是由20oN以北的月平均1000hPa位势高度异常场的EOF第一特征空间向量场确定,第一主模态对应的时间系数为AO指数。利用20oN-90oN的月平均标准化的500mb位势高度异常的RPCA(Rotated Principal Component Analysis)进行分析得到NAO指数。
北大西洋涛动(NAO)指亚速尔高压和冰岛低压之间气压差的反向变化关系,即当亚速尔地区气压偏高时,冰岛地区气压偏低,反之亦然。NAO是北大西洋地区最显著的模态。1998年首次提出北极涛动(AO)的概念(Thompson and Wallace, 1998),用于描述北半球气候变率的主要模态。AO是指中纬度和极区反位相变化的南北振荡形式。AO与NAO在时间和空间特征上都表现出很强的相似性,Wallace(Wallace, 2000)指出,AO与NAO二者本质上是一致的,是同一事物在不同侧面的两种表现,实际上反映的都是中纬度西风的强弱;只不过AO尺度更大,而NAO是其在北大西洋区域的表现。但Chirstiansen(Chirstiansen, 2002)通过非线性分析讨论了AO和平流层变化之间的联系,将它与对流层的NAO区分开来。Kodera and Kuroda (2003) 从物理机制上解释了两者的区别, 认为AO是由对流层和平流层低层的行星波引起极区垂直运动变化而产生的。本文利用美国气候预测中心发布的AO和NAO指数进行傅里叶分析、功率谱分析、小波分析和经验模态分解四种方法,探讨这两种低频变化模态的时间尺度。
原始时间序列
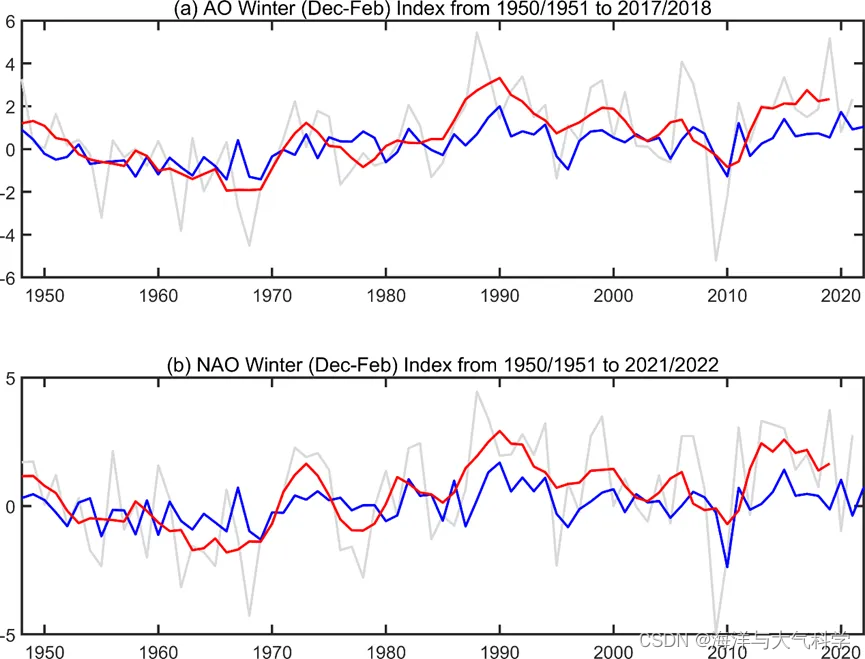
图1为1950/1951-2021/2022年冬季(Dec-Feb)AO月平均指数与NAO月平均指数及冬季平均值及5年滑动平均值。AO冬季指数在1950-1972/73为负相位占主导,正相位持续时间不长,1987-1994期间为正相位。NAO冬季指数呈现明显的多年代际变化(Hurrell 1995, Chelliah and Bell 2005)。1950-1972/73是NAO负相位占主导,1980-2008/09为正相位占主导,进而转入正相位。AO指数较NAO指数变化幅度较大,但整体上两者变化趋势一致。
图片
图 1 1950/1951 至 2021/2022年 AO 冬季(12-2 月)指数和 NAO 冬季(12-2 月)指数的时间序列。灰线为年平均(1-12月)指数,蓝色线条为冬季平均值的指数,红色线为冬季指数的 5 年平均值。
两种滑动相关系数
相关系数方法介绍
相关系数是描述两个不同物理量相关度的量。皮尔逊积距相关系数(Pearson product-moment correlation coefficient)(Pearson, 1896)是描写线性相关度的一种简单相关系数。
3.1.1 结果展示
以本文为例,1950-2022年AO年平均指数与NAO年平均指数的相关系数为0.8318;1950/1951-2021/2022年冬季(Dec-Feb)AO月平均指数与NAO月平均指数的相关系数为0.8799。
3.2 滑动相关系数方法介绍
在时间序列数据的分析中,人们不满足于两个时间序列的整体相关性,而是希望了解两个时间序列相关特性随时间的变化,这就需要计算滑动相关系数,即计算一段时间窗口内的相关系数,并通过移动时间窗口,得到相关系数随时间的变化。局域滑动相关系数(local running correlation coefficient,LRCC)只代表了距平变化的相关性,而合成滑动相关系数(SRCC)才反映了距平和均值都发生变化时的相关性。
3.2.1 结果展示
本文分别计算1950-2022年AO、NAO月平均指数及1950/1951-2021/2022年冬季(Dec-Mar)AO、NAO月平均指数的合成滑动相关系数(SRCC)以及局域滑动相关系数(LRCC),时间窗口分别为3和6。时间窗口为n=3时,滑动相关系数较为粗糙,存在季节变化的成分,而时间窗口为n=6时滤去年周期变化。而且可以观察看出,AO和NAO的相关系数始终保持在高相关。
(1)1950-2022年AO、NAO年平均指数
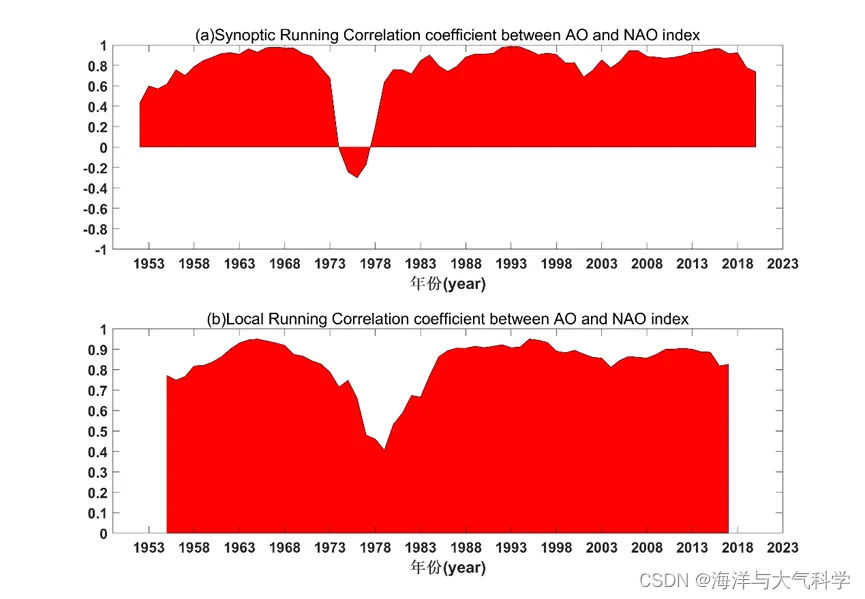
(2)1950-2022年AO、NAO月平均指数
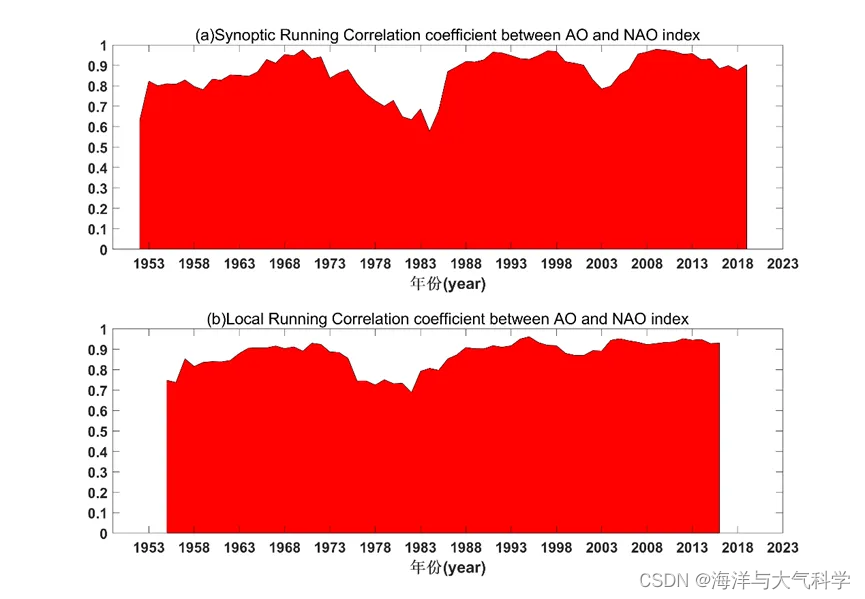
图 2 1950 至 2017 年 AO 与 NAO 指数之间的两个运行相关系数。不同窗宽计算的相关系数(上图nd=3;下图nd=6)。
总结:
时间窗口的选择会影响滑动相关系数的平滑程度,总体上看,各时间跨度的AO与NAO月平均指数的相关性都较好,其中冬季AO与NAO月平均指数相关性最好。根据Zhao and Cao (2018)提出的判断Rs(t)是比Rr(t)更好的滑动相关系数的判据,即:滑动相关系数的平均值应该接近总的相关系数。结果表明,SRCC与总相关系数接近,而LRCC有时差别很大。SRCC完好地体现了不同时段数据之间的可比性,可以真实地表现两个时间序列在物理上的一致程度,被证明是比LRCC更好的滑动相关系数,因而SRCC是比LRCC更好的滑动相关系数。
相关数据代码等资料已上传入群中。

)
)







)

安装docker)






—— Dropout和批归一化)