蓝桥杯

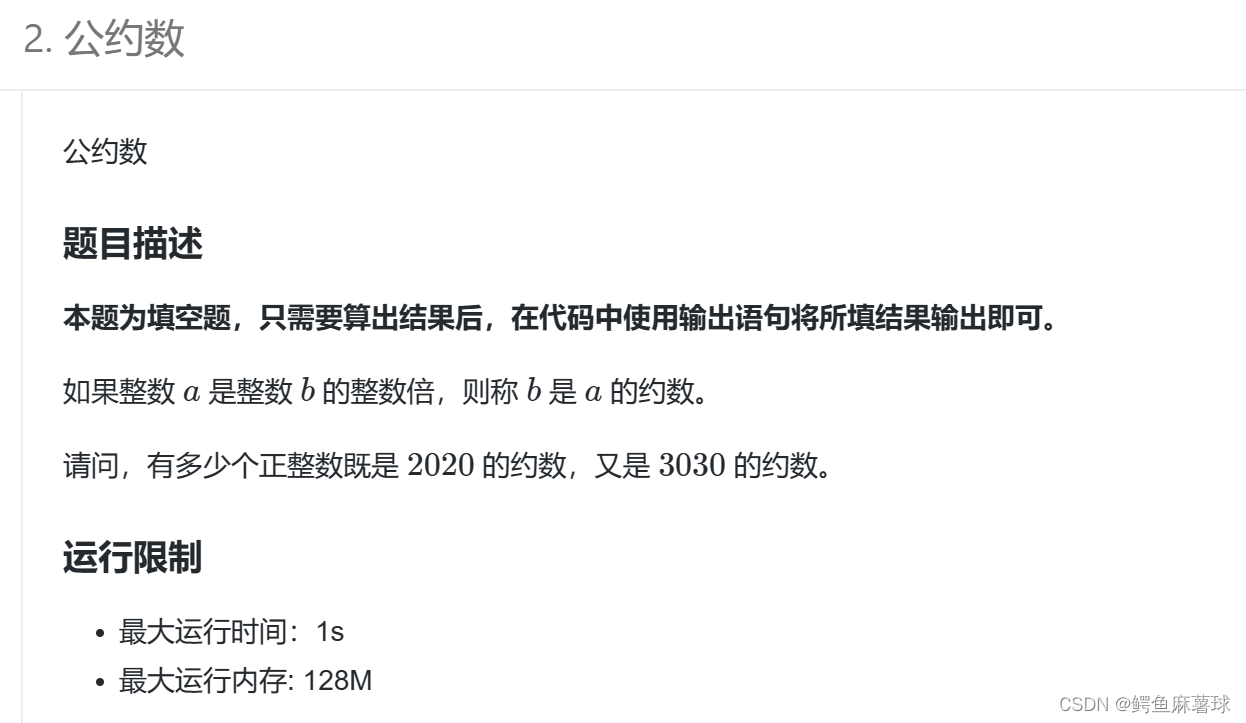
* 最大公约数

  两个整数的最大公约数等于其中较小的那个数和两数的差的最大公约数。通过不断地用较小的数替换较大的数，并用两数的差替换较小的数，最终会得到最大公约数。

  例如，计算 gcd(48, 18) 的过程如下：

  gcd(48, 18)
  gcd(18, 48 % 18) = gcd(18, 12)
  gcd(12, 18 % 12) = gcd(12, 6)
  gcd(6, 12 % 6) = gcd(6, 0)

  当 b 为零时，算法停止，返回 a（在这里是6），这是 48 和 18 的最大公约数。

int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}

  

  对于一些比较难以理解或者自己尝试书写有困难的算法，我们可以理解它的一些简单的例子并且尝试记下来，对于我们直接使用提高做题效率有很大的帮助。

#include <iostream>
using namespace std;int gcd(int a,int b)
{return b?gcd(b,a%b):a;
}int main()
{int ret=0;for(int i=1;i<=3030;i++){if(gcd(i,2020)==i&&gcd(i,3030)==i){ret++;}}cout<<ret;return 0;
}

  

#include <iostream>
using namespace std;int gcd(int a,int b)
{return b?gcd(b,a%b):a;
}int main()
{int n=0;cin>>n;int a=0,b=0;while(n--){cin>>a>>b;cout<<gcd(a,b)<<endl;}return 0;
}

  

#include <iostream>
using namespace std;int gcd(int a,int b)
{return b?gcd(b,a%b):a;
}int main()
{int x=0,y=0;cin>>x>>y;int ret=0;long long xy=x*y;for(int p=x;p<=y;p++){for(int q=x;q<=y;q++){if(q*p==xy&&gcd(q,p)==x){ret++;}}}cout<<ret<<endl;return 0;
}

            

欧拉函数模版

  欧拉函数是计算小于n的正整数中与n互质的数的数目。

// 欧拉函数模版
#include <iostream>
using namespace std;
int main()
{int n;cin >> n;while (n--){int a;cin >> a;int res = a;for (int i = 2; i <= a / i; i++){if (a % i == 0){res = res / i * (i - 1);while (a % i == 0) a /= i;}}if (a > 1) res = res / a * (a - 1);cout << res << endl;}return 0;
}

#include <iostream>
using namespace std;
int main()
{int n;cin>>n;while(n--){int a;cin>>a;int res=a;for(int i=2;i<=a/i;i++){if(a%i==0){res=res/i*(i-1);while(a%i==0) a/=i;}}if(a>1) res=res/a*(a-1);cout<<res<<endl;}return 0;
}

  

* 线性筛法 求欧拉函数

  欧拉函数计算小于或等于某个数 n 的所有正整数的欧拉函数值之和的。 欧拉函数，记作 φ(n)，表示小于 n 且与 n 互质的正整数的个数。

  get_eulers 函数是实现欧拉函数计算的核心部分。它首先初始化 phi[1] = 1，然后遍历从 2 到 n 的所有整数。对于每个整数 i，如果 i 是质数（即 st[i] 为假），则将其添加到 primes 数组中，并设置 phi[i] = i - 1，因为质数的欧拉函数值就是它自身减一。

  接着，对于每个质数 primes[j]，代码会计算 primes[j] * i 的欧拉函数值。这里使用了线性筛法的思想，避免了重复计算。如果 i 能够被 primes[j] 整除，那么 primes[j] * i 的欧拉函数值就是 phi[i] * primes[j]，并且内层循环会提前结束（因为 primes[j] 已经是 primes[j] * i 的一个质因子，无需继续筛选）。否则，primes[j] 是 primes[j] * i 的一个新质因子，所以 primes[j] * i 的欧拉函数值就是 phi[i] * (primes[j] - 1)。

const int N = 1000010;int primes[N], cnt = 0;
int phi[N];
bool st[N];// 线性筛法 求欧拉函数
ll get_eulers(int n)
{phi[1] = 1;for (int i = 2; i <= n; i++){if (!st[i]){primes[cnt++] = i;phi[i] = i - 1; // i如果是质数，那么i的欧拉函数就是i-1}for (int j = 0; primes[j] <= n; j++){st[primes[j] * i] = true;if (i % primes[j] == 0){phi[primes[j] * i] = phi[i] * primes[j]; //第primes[j]*i的 欧拉函数为phi[i]*primes[j] break; // 线性筛法}phi[primes[j] * i] = phi[i] * (primes[j] - 1);}}ll res = 0;for (int i = 1; i <= n; i++) res += phi[i];return res;
}int main()
{int n = 6;cout << get_eulers(n) << endl;return 0;
}

  

* 快速幂 a^k%p

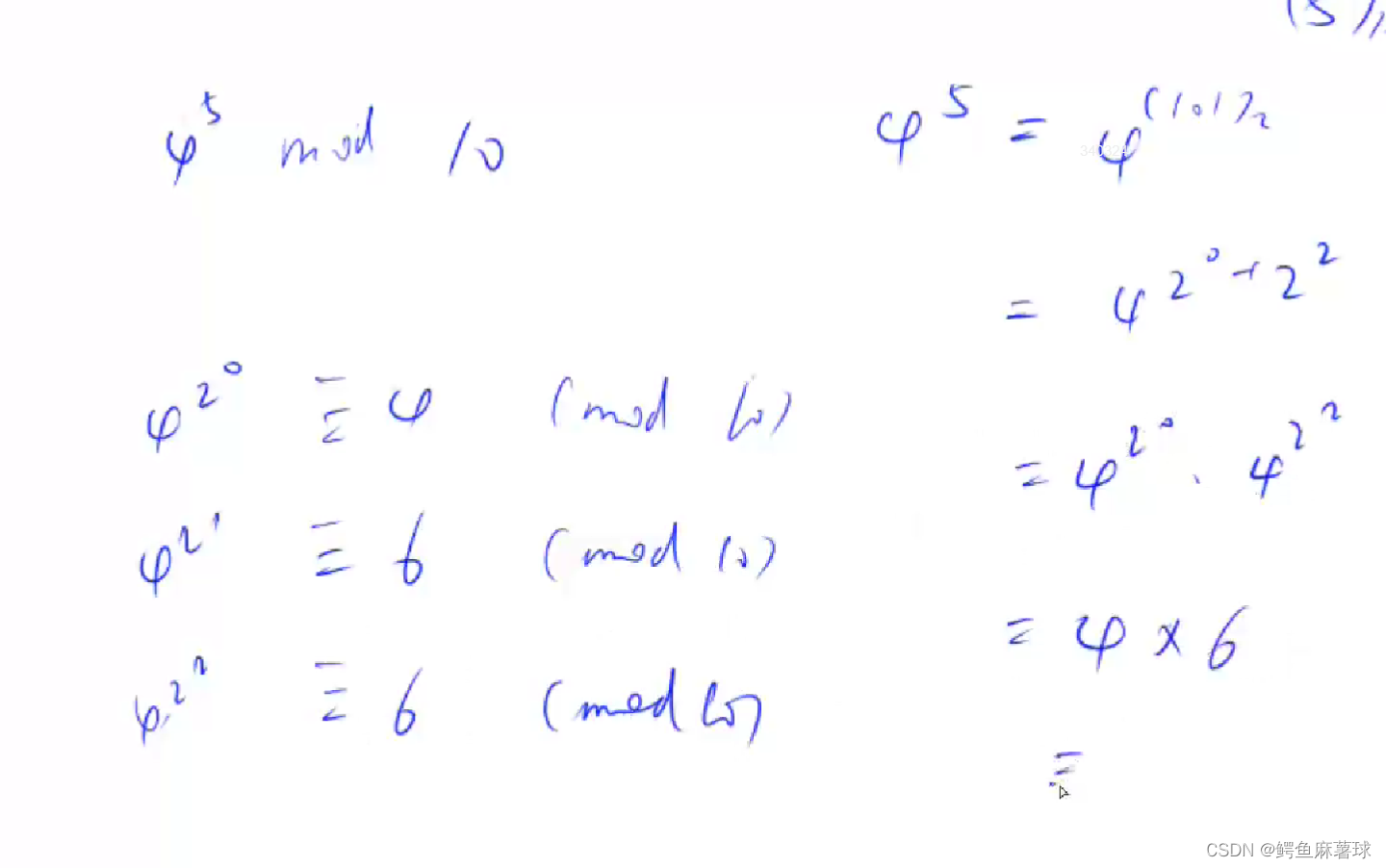
  if (k & 1) res = (ll)res * a % p;：如果 k 的二进制表示的最低位是 1，那么将 a 乘到 res 上，并对 p 取模。这里 (ll) 是为了将 res 和 a 转换为 long long 类型，以防止在计算过程中溢出。

  k >>= 1;：将 k 右移一位，相当于除以 2。

  a = (ll)a * a % p;：将 a 自乘，并对 p 取模。

// 快速幂 a^k%p
int qmi(int a, int k, int p)
{int res = 1;while (k){if (k & 1)res = (ll)res * a % p;k >>= 1;a = (ll)a * a % p;}return res;
}int main()
{int n=1;//cin >> n;while (n--){int a, k, p;cin >> a >> k >> p;cout << qmi(a, k, p);}return 0;
}

  

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;// 快速幂 a^k%p
int qmi(int a, int k, int p)
{int res = 1;while (k){if (k & 1)res = (ll)res * a % p;k >>= 1;a = (ll)a * a % p;}return res;
}int main()
{int n=1;//cin >> n;while (n--){int a, k, p;cin >> a >> k >> p;cout << qmi(a, k, p);}return 0;
}

  

扩展欧几里得算法

  除了计算a、b两个整数的最大公约数，此算法还能找到整数x、y。通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 a 与 b, 必存在有整数 x 与 y 使得ax + by = gcd(a,b)。

// 扩展欧几里得算法
int exgcd(int a, int b, int& x, int& y)
{if (!b){x = 1, y = 0;return a;}int d = exgcd(b, a % b, y, x);y -= a / b * x;return a;
}int main()
{int n;cin >> n;while (n--){int a, b, x, y;cin >> a >> b;exgcd(a, b, x, y);cout << x << " " << y;} return 0;
}