在大气表面层( atmospheric surface layer)中,MO参数是用来决定流动是中性或者非中性的一个重要参数。其定义是 z / L z/L z/L,其中 L L L为Obukhov长度,其含义是浮力产生的湍动能和剪切产生的湍动能之比(Hj h AIP 2023)(Monin IAS,1954),具体公式如下:

上面的公式中 Q Q Q为总热通量,包括对流传热热通量和热传导热通量。
根据我之前写过的计算Nu数的博客中,由具体公式
其有量纲形式如下
v T − α ∂ T / ∂ y vT-\alpha \partial T/\partial y vT−α∂T/∂y
Pirozzoli的文章中又另一个L的计算公式,其特别指出形式上与典型的L计算方法不同。

在KADER 1990 JFM中,也有相关定义,分别上面两种定义一致

这里插一句,这里热膨胀系数等于平均温度的倒数,我实验了一下,确实是,但是其原因并不清楚,从课程PPT中也看不出来,太菜了,,,

除此之外,还有另一种Obukhov长度计算方法,来自Hongyou Liu JFM 2022

而且Liu还计算了每个时刻的L,其应该是计算L时只进行了空间平均的操作。
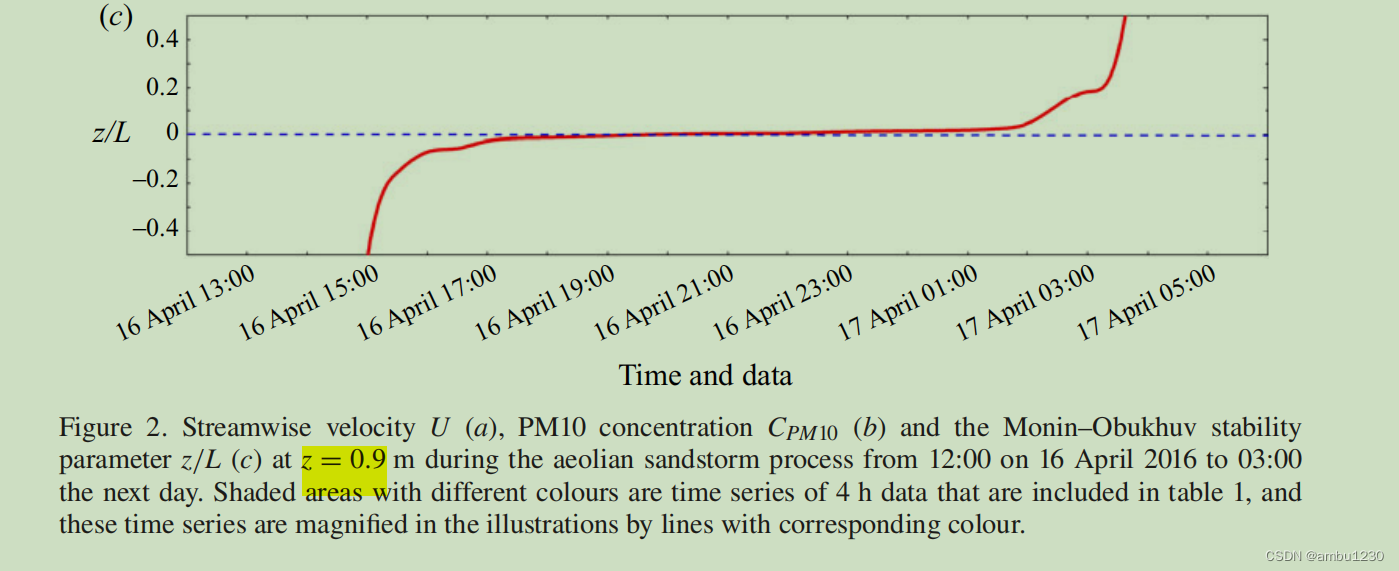
而且,其没有出现热膨胀系数,而是用平均温度来代替,KADER 1990 JFM的说法来看,这两者是等价的。
但是Liu将上面的热通量Q采用湍流热通量代替,即文中说是温度脉动和速度脉动的协方差,这个操作来源于Kapil Boundary-Layer Meteorol 2013,这个存在两个问题,
第一,没有包含热传导引起的热通量
第二,对流热通量不等于湍流对流热通量
第二点,在RB对流系统中是可以划等号的
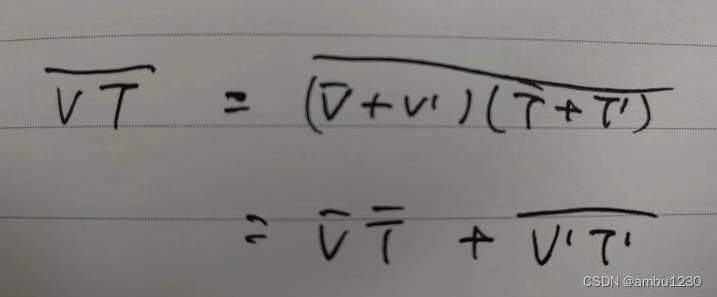
因为系统是上下对称的,平均场中, v ‾ T ‾ \overline{v}\overline{T} vT是等于0 的,但是对于大气边界层这类复杂的问题,显然这一项不等于0,那他们为啥还要这样做。
第一项热传导需要测量温度梯度,这一项对于试验可能很难得到,但是直接测量温度和速度得到对流热通量还是可以的吧,那为啥要用湍流热通量代替呢。不晓得,这帮人,写文章连最基本的Obukhov长度都不统一,无语死,这点东西看了一下午。



ALU)
 并查集)




)









主存)