【TD3思路及代码】【自用笔记】

1 组成（Target Network Delayed Training）

Actor网络：这个网络负责根据当前的状态输出动作值。在训练过程中，Actor网络会不断地学习和优化，以输出更合适的动作。
Critic网络：TD3中有两个Critic网络，也称为Twin Critic。这两个网络的主要功能是评估Q值（action的未来奖励值），也就是根据给定的状态和动作来估计未来的奖励。使用两个Critic网络可以减小估计的Q值的方差，使结果更加稳定。

目标网络：TD3还引入了目标网络的概念。目标网络是Actor和Critic网络的副本，它们用于在训练过程中提供稳定的目标值。这有助于防止训练过程中的震荡和不稳定。

2 特点

回放缓冲区（replay buffer）：Replay Buffer 是一个固定大小的循环队列，用于存储智能体与环境交互产生的经验（experience），四元组数据包含了不同时间步长的状态、动作、奖励和下一个状态（s,a,r,s_）。通过这些数据，TD3能够学习到如何在给定的状态下选择最优的动作，以最大化未来的奖励。 - store_transition()方法
TD3采用了截断双Q学习、在目标策略网络中加入噪声以及降低策略网络和目标网络的更新速度等策略，以进一步提高算法的稳定性和性能。
random noisy：指的是随机生成噪声，用于增加动作的多样性，避免策略过于稳定。体现：
MLP多层感知机（Multi-Layer Perceptron）：是一种基于神经网络的分类器，常用于解决分类问题。MLP 中的一层由若干个神经元组成，每个神经元接收上一层的输出，并对其进行加权和，再经过激活函数进行非线性变换。MLP 层可以被看作是一种前向传播过程，它将上一层的输出作为输入，经过若干次变换，最后得到输出结果。
在TD3中，有主网络+目标网络，每个网络又分别包含策略网络和Q值网络，主网络在训练过程中不断地更新其权重和偏置，通过梯度下降等优化算法直接更新参数，目标网络通过定期地从主网络中复制得到，polyak加权平均的以更新。这种定期复制参数的方式确保了目标网络能够跟随主网络的进步，同时又保持了相对的稳定性（训练会不太稳定）。这是因为目标网络在一段时间内是固定的，所以它提供的目标Q值是稳定的，这有助于减少训练过程中的波动，提高算法的稳定性。

3 代码
tf.placeholder是一个用于定义输入数据的占位符。当运行TensorFlow的会话（session）时，你需要为这些占位符提供实际的值。
self.x_ph = tf.placeholder(tf.float32, [None, obs_dim])
x_ph是一个占位符，本代码定义这个占位符，假设obs_dim是10，那么你可以为self.x_ph提供形状为[1, 10]、[10, 10]、[100, 10]等的张量，只要它们是浮点数类型且第二个维度是10。reward一般写为[None,] ，定义了一个一维张量，其长度可以是任意的，一般为批次大小。同时注意区分：
tf.variable_scope('main')定义了一个用于Actor-Critic方法的神经网络结构
with tf.variable_scope('main'):self.pi, self.q1, self.q2, self.q1_pi = mlp_actor_critic(self.x_ph, self.a_ph, **ac_kwargs)
    actor网络pi输出动作（策略）；两个critic网络q1、q2输出动作的q值；q1_pi也是一个critic网络，输出pi输出的动作的q值
最后是输出动作（策略）的q值
神经网络细节：hidden_sizes 是一个元组（tuple），它定义了多层感知机（MLP）中隐藏层的尺寸（即每个隐藏层中的神经元数量）。例如，如果 hidden_sizes=(400, 300)，那么 MLP 将有两个隐藏层，第一层有 400 个神经元，第二层有 300 个神经元。 list(hidden_sizes)+[act_dim] 的作用是将 hidden_sizes 元组转换为列表，并在其后追加一个新的元素 act_dim。这里的 act_dim 是动作空间的维度，即输出层的神经元数量。 list(hidden_sizes)+[act_dim] 则定义了整个神经网络（包括2个400尺寸和300尺寸的隐藏层和动作数量尺寸的输出层）的层尺寸。
一些参数含义及选择

4 步骤

4.1 initTD3
net = TD3(a_dim, s_dim, a_bound,batch_size=64)
（1）定义占位符x_ph(主网络S)、x2_ph(目标网络S)、a_ph(A)、r_ph(R)、d_ph(Done)
self.x_ph = tf.placeholder(tf.float32, [None, obs_dim])  # 输入self.x2_ph = tf.placeholder(tf.float32, [None, obs_dim])self.a_ph = tf.placeholder(tf.float32, [None, a_dim])  # actionself.r_ph = tf.placeholder(tf.float32, [None,])  # rewardself.d_ph = tf.placeholder(tf.float32, [None,])  # done标识
（2）定义主网络的actor-critic神经网络：actor策略网络pi输出动作，两个criticQ值网络q1、q2输出动作的q值(减少过估计)，q1_pi也是一个critic网络，输出pi输出的动作的q值。
with tf.variable_scope('target'):# 只关心第一个返回值pi_targ，它代表了目标策略网络的输出pi_targ, _, _, _ = mlp_actor_critic(self.x2_ph, self.a_ph, **ac_kwargs)
（3）定义目标网络的actor策略网络：只关心目标actor策略网络pi_targ的输出动作。（pi_targ 是一个与原始策略网络 pi 结构相同的神经网络输出，但它的权重在训练过程中会以不同的方式更新（通常是缓慢地跟踪原始网络的权重）。这种延迟更新的目标网络有助于稳定学习过程，因为它提供了一个更一致的目标来优化原始网络。在TD3中，目标网络通常用于计算目标Q值，这些目标Q值然后用于训练原始Q值网络。这种方法有助于减少过估计问题，提高算法的稳定性和性能。）

（4）目标策略平滑：在目标策略 pi_targ 上添加噪声 epsilon（噪声 epsilon 是一个正态分布，其均值为 0，标准差为 target_noise，最终将噪声大小修建到noise_clip范围内），添加后创建了一个新的动作 a2，修建到action_bound范围内。（目标策略平滑是一种正则化技术，它有助于减少过拟合，并鼓励算法探索不同的动作。在TD3中，它还可以帮助减少由于函数近似误差引起的Q值估计的过高问题。）

（5）定义目标网络的criticQ值网络：输入修改后的动作 a2（目标策略平滑后的策略）和状态，计算目标Q值 q1_targ 和 q2_targ。这些目标Q值将用于训练原始Q值网络。
 with tf.variable_scope('target', reuse=True):# 生成均值为0方差为target_noise的噪声epsilon = tf.random_normal(tf.shape(pi_targ), stddev=target_noise)# 噪声值被裁剪到[-noise_clip, noise_clip]的范围内epsilon = tf.clip_by_value(epsilon, -noise_clip, noise_clip)# 在目标策略pi_targ上添加噪声epsilona2 = pi_targ + epsilon# 加了噪声的动作再次被裁剪到动作空间的界限[-self.act_limit, self.act_limit]内a2 = tf.clip_by_value(a2, -self.act_limit, self.act_limit)# 输入平滑后的动作定义目标Q值网络_, q1_targ, q2_targ, _ = mlp_actor_critic(self.x2_ph, a2, **ac_kwargs)
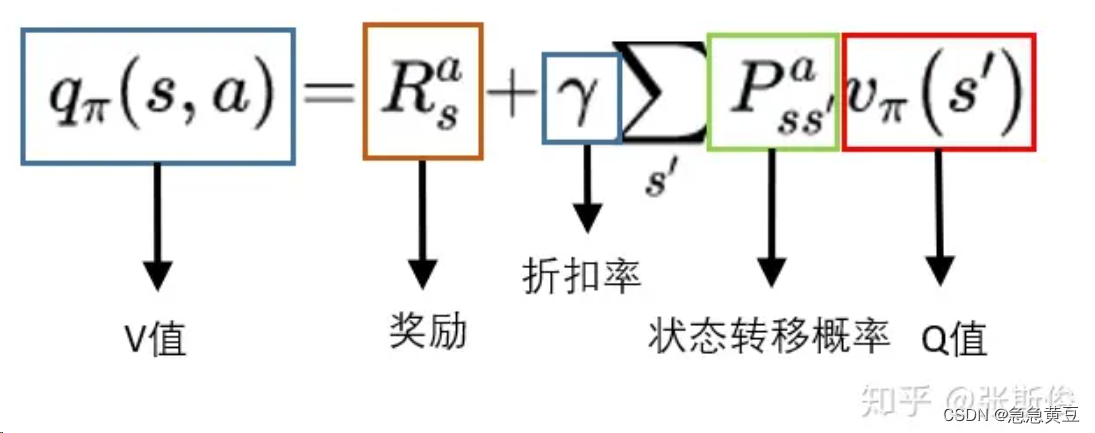
（6）取q1_targ 和 q2_targ这两个估计中的最小值作为最终的Q值目标。这样做可以进一步减少过估计的风险。
min_q_targ = tf.minimum(q1_targ, q2_targ)
（7）Bellman备份操作，描述了状态-动作值函数（Q函数）的递归更新规则。当前状态-动作对的值可以通过加上奖励（self.r_ph）和折扣后的下一个状态的最大Q值（gamma * (1 - self.d_ph) * min_q_targ）来计算。（当self.d_ph为1时，表示当前状态是终止状态，没有未来的奖励或状态）。同时使用tf.stop_gradient阻止梯度传播，不需要对备份backup变量进行梯度计算，因为它只是用于计算损失函数，而不是用于更新网络权重。
# Bellman备份并阻止梯度传播
backup = tf.stop_gradient(self.r_ph + gamma * (1 - self.d_ph) * min_q_targ)
（8）计算损失函数policy loss和Q-Value losses。

- 策略损失是策略网络输出的动作在Q网络中的Q值（q1_pi）期望的负数，策略网络的目标是最大化这个Q值，即选择能导致高回报的动作。因为优化器通常用于最小化损失，所以取负值来将问题转化为最小化问题。tf.reduce_mean 用于计算所有样本的平均损失。

- Q值损失是通过计算Q网络估计的两个Q值q1、q2与目标Q值（backup）之间的均方误差（MSE）来得到的。这样，通过最小化Q值损失，Q网络会逐渐学习到更准确的Q值估计。
self.pi_loss = -tf.reduce_mean(self.q1_pi)
q1_loss = tf.reduce_mean((self.q1 - backup) ** 2)
q2_loss = tf.reduce_mean((self.q2 - backup) ** 2)
self.q_loss = q1_loss + q2_loss
（9）定义策略网络优化器和Q值网络优化器，使用策略网络优化器来最小化策略损失函数pi_loss，指定了应该更新变量为主网络的策略网络main/pi；使用策略网络优化器来最小化策略损失函数pi_loss，指定了应该更新变量为主网络的策略网络main/pi
# 定义策略网络优化器
pi_optimizer = tf.train.AdamOptimizer(learning_rate=pi_lr)
# 定义Q值网络优化器
q_optimizer = tf.train.AdamOptimizer(learning_rate=q_lr)
# 使用pi_optimizer优化器来最小化self.pi_loss，指定了应该更新变量'main/pi'
self.train_pi_op = pi_optimizer.minimize(self.pi_loss,var_list=get_vars('main/pi'))
# 使用q_optimizer 优化器来最小化self.q_loss，指定了应该更新变量'main/q'
self.train_q_op = q_optimizer.minimize(self.q_loss,var_list=get_vars('main/q'))
（10）Polyak 平均用于目标变量的更新：目标网络的参数v_targ被更新为当前v_targ（0.995）和主网络参数v_main（0.005）的加权和，使得目标网络参数的变化比主网络更加平滑。polyak用于控制目标网络参数更新的速度，越小就变得越慢。
self.target_update = tf.group([tf.assign(v_targ, polyak * v_targ + (1 - polyak) * v_main)for v_main, v_targ in zip(get_vars('main'), get_vars('target'))])
（11）将目标网络的参数初始化为与主网络相同。这是训练开始时的常见做法，以确保两者在开始时是同步的。
target_init = tf.group([tf.assign(v_targ, v_main)for v_main, v_targ in zip(get_vars('main'), get_vars('target'))])
（12）TensorFlow 会话和变量初始化，执行（11）
# 创建一个TensorFlow会话
self.sess = tf.Session()
# 初始化所有全局变量
self.sess.run(tf.global_variables_initializer())
# 将目标网络的参数初始化为与主网络相同。
self.sess.run(target_init)
4.2 get_action方法：用于根据当前的状态 s 来选择一个动作，并在需要时添加一些噪声。给定一个缩放比例action_noise（noise_scale）为0.1

4.3 store_transition()方法：对1得到的a放入step中执行+随机事件影响=新的状态s_和奖励r，将（s,a,r,s_）放入replay buffer。

4.4 learn()方法：

- 算法从 Replay Buffer 中随机采样一小批经验用于更新Q值网络和策略网络（actor network）。这种随机采样有助于打破经验之间的相关性，使得训练更加稳定。从回放缓冲区中随机抽取一个大小为batch_size（64）的批次数据。

- 根据抽取的批次数据构建一个字典feed_dict

- Q值网络的更新：将字典中的数据依次喂给step进行q网络更新，每次都计算q1、q1的qloss（8）、更新q网络（9）

- 策略网络的更新（延迟更新）：只有当 self.learn_step 是 self.policy_delay 的整数倍时，才会更新策略网络。这有助于稳定训练过程，因为Q值网络通常比策略网络更容易训练。此外，除了更新策略网络，还执行了目标网络的更新 self.target_update（10），这是为了保持目标网络的稳定性。

** 延迟更新好处：在策略网络的更新和Q值网络的更新之间加入了一个时间差。这意味着Q值网络有更多的机会收敛到一个较为稳定和准确的预测，然后再将这些预测用于更新策略网络。这样，策略网络可以在更可靠的信息基础上进行更新，有助于减少由于Q值网络的不稳定性而导致的错误更新。

5 一些问题

为什么只优化主网络的策略网络和Q值网络，并不优化目标网络？

        目标网络在TD3中的主要作用是提供一个稳定的目标Q值来计算损失。在训练过程中，如果直接优化目标网络，那么目标Q值将会变得不稳定，从而影响训练的稳定性和收敛性。因此，在TD3中，我们固定目标网络的参数一段时间（例如，每更新几次主网络后，才更新一次目标网络），这样可以确保目标Q值在一段时间内是稳定的。这样，我们就可以在稳定的目标Q值基础上，优化主网络的Q值网络和策略网络。虽然不直接优化目标网络，但是通过定期将主网络的参数复制到目标网络，间接地实现了目标网络的更新。这种更新方式确保了目标网络的稳定性，同时又能跟上主网络的进步。

为什么目标网络是先通过策略网络生成动作a，再将经过平滑处理的a值送入Q值网络？

        在TD3中，目标网络的目的是提供一个稳定的目标Q值。首先，目标策略网络根据下一个状态生成一个动作，这个动作是通过策略网络的输出得到的。然后，这个动作会被加上一个小的噪声（通常是裁剪的正态分布噪声），以鼓励探索并减少过估计问题。最后，这个经过平滑处理的动作被送入目标Q值网络，以计算目标Q值。（理解为目标网络是给出结果，但主网络是给出a以及通过已知数据s、a、s_、r对两个网络进行更新，没有先后过程）

        主网络同时接收动作和状态，是因为主网络需要同时更新策略网络和Q值网络。策略网络用于生成当前状态下的动作，而Q值网络则用于评估这个动作的价值。这两个网络的输出共同决定了当前策略的好坏，因此需要同时更新。

为什么计算出来两个主Q值网络的损失之后，要将他们加起来？

        TD3使用两个Q值网络（Q1和Q2）来减少过估计问题。每个Q值网络都会独立地计算一个Q值，并分别计算损失。将这两个损失相加后，再进行反向传播更新网络参数。这样做的目的是同时优化两个Q值网络，确保它们都能提供准确的Q值估计。通过取两个Q值网络的最小值作为当前策略的Q值，可以进一步减少过估计问题。

为什么要对目标网络进行Polyak平均？

Polyak平均（也称为软更新）是一种平滑地更新目标网络参数的方法。在TD3中，目标网络的参数不是直接复制主网络的参数，而是通过一个较小的学习率（例如0.005）来逐步接近主网络的参数。这种更新方式确保了目标网络的稳定性，同时又能跟上主网络的进步。Polyak平均可以有效地减少训练过程中的波动，提高算法的稳定性。

         2. 反向传输

        在深度学习中，反向传播（Backpropagation）是一个用于训练神经网络的重要算法。它的核心思想是通过计算损失函数对模型参数的梯度，从输出层反向传递梯度信息，以便更新模型参数，从而最小化损失函数，使模型更好地拟合训练数据。

具体到“将这两个损失相加后，再进行反向传播更新网络参数”这一步骤，我们可以这样理解：

        首先，在训练神经网络时，通常会定义一个损失函数来表示预测值与实际值之间的误差。在这个场景中，由于有两个Q值网络（Q1和Q2），因此会有两个对应的损失函数，分别计算Q1和Q2网络的预测误差。

        接下来，这两个损失函数会分别计算出各自的损失值，然后将这两个损失值相加，得到一个总的损失值。这个总的损失值就代表了整个神经网络在当前状态下的预测误差。

        然后，进入反向传播阶段。在这个阶段，算法会使用链式法则来计算损失函数对每个模型参数的梯度。这些梯度表示了参数对损失函数的影响程度，即如果稍微调整这些参数，损失函数会如何变化。

        最后，根据计算出的梯度，使用优化算法（如梯度下降）来更新网络的参数。通过不断迭代这个过程，神经网络会逐渐学习到如何更好地拟合训练数据，从而提高预测性能。