0322. 零钱兑换 

题目：

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。

基本思路：将金币从大到小开始排列，先拿最大的，再拿后面次大的，以此类推。【失败】

class Solution {
public:int coinChange(vector<int>& coins, int amount) {sort(coins.begin(),coins.end());int size=coins.size();if(amount==0) return 0;int ans=0;int remains=amount;for(int i=size-1;i>=0;i--){while(remains>=coins[i]){remains-=coins[i];ans++;}}return (remains>0)?-1:ans;}
};

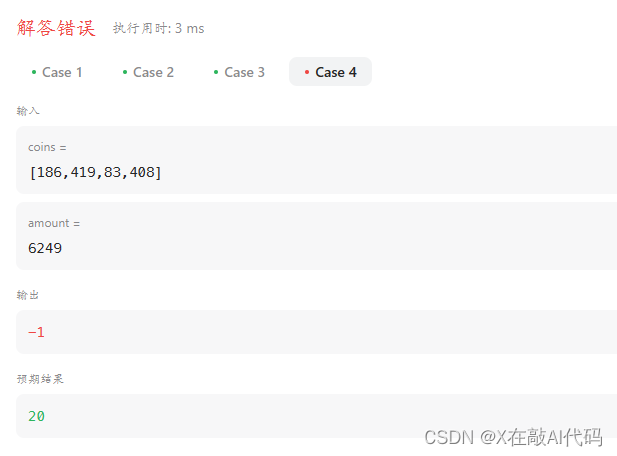
但显然有bug，思考一顿发现，他可能不需要最后一个，可以是倒数第二个拼起来 ，例如上面这个例子3+4可以出现7但运行时依然把5放上了：

所以进行改进： 如果再进行一层遍历，便从哪一个开始，显然复杂度太高。

这个时候想到了，动态规划。

创建了一个长度为 amount+1 的数组 dp，dp[i] 表示凑齐金额 i 所需的最少硬币数目。然后通过迭代更新 dp 数组，最终返回 dp[amount]。如果 dp[amount] 大于 amount，则表示无法凑出总金额，返回 -1。

代码：

class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, amount + 1);dp[0] = 0; // if(amount==0)return 0;for (int i = 1; i <=amount; i++) {for (int j = 0; j < coins.size(); j++) {if (coins[j] <= i)//硬币数值小于总数dp[i] = min(dp[i],dp[i-coins[j]]+1);//可以选择放还是不放。}}return dp[amount]>amount?-1:dp[amount];}
};

每一次dp都可以选择放还是不放。不放就是dp[i]=dp[i];放的话，首先数量要＋1，谁的数量呢？是（当前存放金钱总额-放入的金币额 ）所需的数量加1。

vector<int> dp(amount + 1, amount + 1);

创建了一个名为 dp 的整型向量（vector），并初始化该向量的大小为 amount + 1，所有元素的初始值都设置为 amount + 1。

具体来说，这行代码创建了一个大小为 amount + 1 的整型向量 dp，并且用 amount + 1 来填充所有的元素。在动态规划问题中，通常会使用类似这样的数组来记录中间状态或者保存子问题的解，以便后续计算。在这个特定的动态规划问题中，dp[i] 代表凑齐金额 i 所需的最少硬币数量，初始值设为 amount + 1 也是为了确保后续更新时能正确比较和更新数值。

本题over

---

78. 子集

题目：

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

思路：这道题自己想的就是遍历。思考用两层for循环，控制左右界限，放之间的元素。后来的时候，又看到一个题解

遍历枚举：

大概意思是：最外层遍历数组的元素，内层循环：复制上一步的子集，然后将当前元素加到复制的子集里面 ，构成新的子集。

举个例子：比如{1,2,3} ：

• 我先产生{1}的子集--》ans={{}，{1}}，
• 我复制这个子集subset={{}，{1}}；此时数组元素遍历到‘2’；
• 把‘2‘’这个元素加到subset里面subset={{2}，{1，2}}；
• 把subset’这个元素加到ans里面此时ans={{}，{1}，{2}，{1，2}}
• 3同理  1）subset={{}，{1}，{2}，{1，2}}；2）subset={{3}，{1，3}，{2，3}，{1，2，3}}
• 3）ans={{}，{1}，{2}，{1，2}，{3}，{1，3}，{2，3}，{1，2，3}}

代码 

class Solution {
public:// 生成一个整数数组的所有可能子集vector<vector<int>> subsets(vector<int>& nums) {// 初始化结果集，包含空集vector<vector<int>> ans = {{}};// 遍历原数组中的每个元素for (int num : nums) {// 获取当前结果集的大小int n = ans.size();// 遍历当前结果集中的每个子集for (int i = 0; i < n; ++i) {// 复制当前子集vector<int> subset = ans[i];// 将当前元素加入子集中subset.push_back(num);// 将更新后的子集加入结果集ans.push_back(subset);}}// 返回生成的所有子集return ans;}
};

二进制位法 

还有使用二进制位来编写的，看了半天没看懂，后来求助解释一下吧

• 对于长度为 n 的原始数组，通过遍历 0 到 2^n - 1 的所有数字，可以表示所有可能的子集。
• 在内层循环中，根据当前数字 i 的二进制表示中的 1，将对应位置的元素加入当前子集。
• 最终将每个生成的子集添加到结果集中，得到所有可能的子集

举个例子

当我们具体遍历生成子集的过程时，以数组 {3,2,1} 为例：当 i = 0 时，二进制表示为 000，对应空集 {}。内层循环不执行，因为没有任何元素被选中。
当 i = 1 时，二进制表示为 001，对应子集 {3}。内层循环执行，检查第 0 位是否为 1，发现是，将 nums[0]（即 3）加入到当前子集中。
当 i = 2 时，二进制表示为 010，对应子集 {2}。内层循环执行，检查第 1 位是否为 1，发现是，将 nums[1]（即 2）加入到当前子集中。
当 i = 3 时，二进制表示为 011，对应子集 {2, 3}。内层循环执行，检查第 0 和第 1 位是否为 1，发现都是，将 nums[0] 和 nums[1] 加入到当前子集中。
当 i = 4 时，二进制表示为 100，对应子集 {1}。内层循环执行，检查第 2 位是否为 1，发现是，将 nums[2]（即 1）加入到当前子集中。
当 i = 5 时，二进制表示为 101，对应子集 {1, 3}。内层循环执行，检查第 0 和第 2 位是否为 1，发现第 0 位和第 2 位为 1，将 nums[0] 和 nums[2] 加入到当前子集中。
当 i = 6 时，二进制表示为 110，对应子集 {1, 2}。内层循环执行，检查第 1 和第 2 位是否为 1，发现第 1 位和第 2 位为 1，将 nums[1] 和 nums[2] 加入到当前子集中。
当 i = 7 时，二进制表示为 111，对应子集 {1, 2, 3}。内层循环执行，检查所有位都为 1，将所有元素 {1, 2, 3} 加入到当前子集中。
通过这样的遍历过程，我们可以逐步生成出数组 {1, 2, 3} 的所有可能子集。

代码： 

class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> ans; // 存储所有可能的子集int n = nums.size(); // 原始数组的长度// 遍历所有可能的子集长度for (int i = 0; i < (1 << n); i++) {vector<int> subset; // 当前子集// 对于每个子集长度，遍历原始数组for (int j = 0; j < n; j++) {// 检查第 j 位是否在当前子集中if (i & (1 << j)) {subset.push_back(nums[j]); // 将元素加入当前子集}}ans.push_back(subset); // 将当前子集加入结果集}return ans;}
};

 其实这道题最最重要的是回溯思想！！

• .  -. - 力扣（LeetCode）总结了回溯问题类型，带你搞懂回溯算法(大量例题)
• 看这个题解就可以

本题over

221. 最大正方形

思想：动态规划

我们可以使用动态规划来解决这个问题。以

假设我们有一个二维矩阵 matrix，其中每个元素是 '0' 或 '1'。我们定义一个额外的二维数组 dp 来存储在以当前位置为右下角的情况下的最大正方形边长。

1. 首先，将 dp 数组初始化为与原始矩阵相同大小，类型为整数。将第一行和第一列直接复制为原始矩阵的值（因为在边界上无法形成正方形）。

2. 对于其余位置 (i, j)，如果 matrix[i][j] 是 '1'，则考虑它左侧、上方和左上方三个位置的 dp 值，取它们的最小值并加 1，即 dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1。

3. 在更新 dp 的过程中，记录下出现的最大边长值，即可得到最大正方形的边长。

4. 最后，返回最大正方形的面积，即边长的平方。

这样，通过动态规划算法，我们可以高效地找到给定矩阵中的最大正方形的边长。

dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1。
如图，当dp[i][j] 来存储在以当前位置[i][j]为右下角的情况下的最大正方形边长时，
dp的值就与上[i-1][j] 左[i][j-1] 左上[i-1][j-1]三个位置的dp相关。看图可以发现与他们最小值相关。
为什么要加1，因为当前位置计算的话，可定是1，可以构成一个小正方形

图解 

代码如下：一定要分清行列

class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {int n = matrix.size();int m = matrix[0].size();if (m == 0 || n == 0)return 0;int max_len = 0;vector<vector<int>> dp(n, vector<int>(m));for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (matrix[i][j] == '1') {if (i == 0 || j == 0) {//第一行第一列dp值=matrix值dp[i][j] = 1;} else {dp[i][j] = min({dp[i - 1][j], dp[i][j - 1],dp[i - 1][j - 1]}) +1;}max_len = max(max_len, dp[i][j]);}}}return max_len * max_len;}
};