概念

1.为了解决二叉搜索树有序插入，会退化成链表，导致效率低下。

AVL树的左右子树高度差不超过1，所以AVL树的查找效率为logn。

2.在左子树高度增加，平衡因子减一，在右子树高度增加，平衡因子加一。

节点的定义

template<class key, class value>struct TreeNode{typedef TreeNode Node;TreeNode< key, value>* left;TreeNode< key, value>* right;TreeNode< key, value>* _parent;std::pair <key, value> data;int bf;//平衡因子TreeNode(const std::pair<key, value>& kv = kv()):left(nullptr), right(nullptr), _parent(nullptr), data(kv), bf(0){}};

插入

这种情况是最简单的情况，只需找到插入位置即可，

当插入节点小于当前节点，那么去左子树找插入位置。

插入节点大于当前节点，那么去右子树寻找插入位置。

当前节点为空时，就是插入位置。

调平衡因子

1.插入之后树高度不变

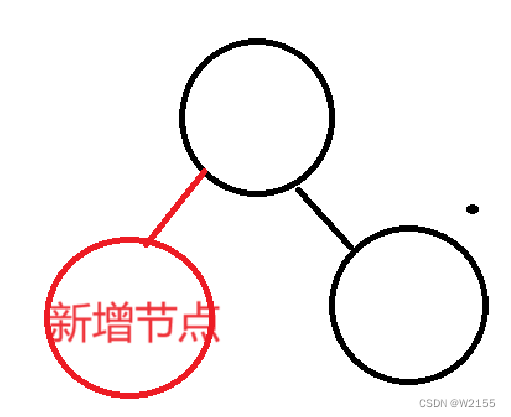
这种情况插入只会影响父亲，不会影响祖先。

所以只需要修改父亲的平衡因子。

2.插入之后，高度增加

这种情况，树的高度增加，会影响整棵树的平衡因子，需要一直向上调整，直到当前节点为根节点。

旋转

在向上调节平衡因子的时候，发现|bf| > 1 ,进行旋转。

1.父亲和孩子在一条直线上

调节到黑色节点时bf == -2，进行右旋转，bf == 2 ，进行左旋转。

将橙色节点，连入黑色的左节点

黑色节点变为红色的右节点

红色在与黑色的父亲节点连接，没有父亲父亲节点变为nullptr

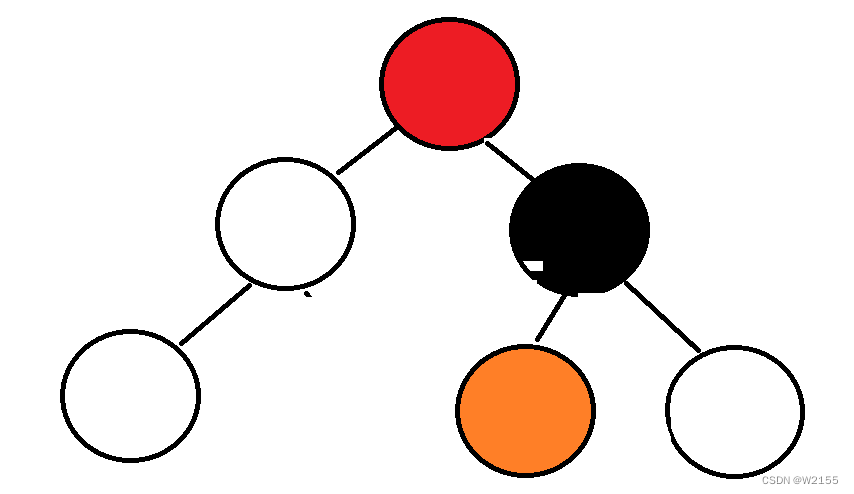
将黑色节点，和红色节点的平衡因子置为0。

2.父亲和孩子不在同一条直线上

如果只进行一次右旋还是会不平平衡。

调节到黑色节点时bf == -2，进行左右双旋转，bf == 2 ，进行右左双旋转。

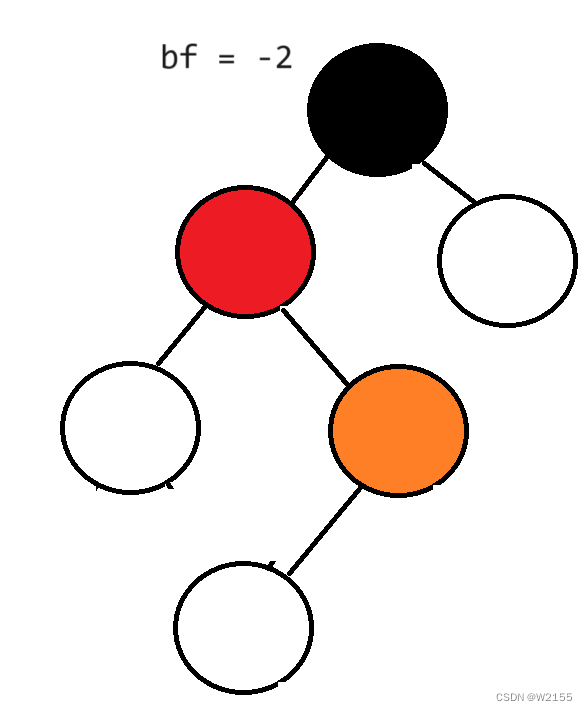
先对红色节点进行一次左旋

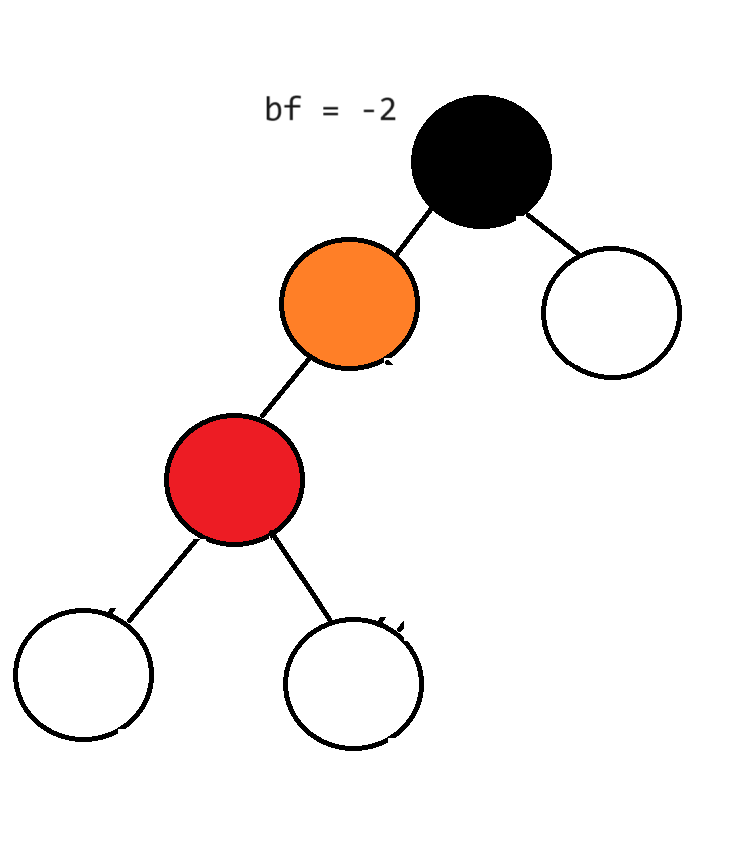
在对黑色节点进行一次右旋

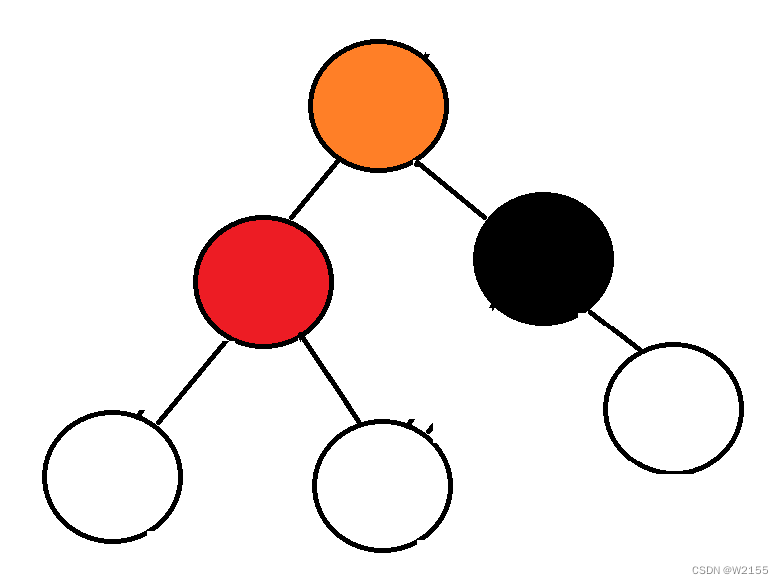
最后调平衡因子分三种情况

经过上图发现，橙色的左节点，变成了红色的右节点。

橙色的右节点，变成黑色的左节点。

1.当橙色的bf == -1

红 bf = 0

黑 bf = 1

橙 bf = 0

2.当橙色bf == 1

红 bf = -1

黑 bf = 0

橙 bf = 0

3.当橙色bf == 0 说明橙是新插入节点

红 bf = 0

黑 bf = 0

橙 bf = 0

完整代码

#pragma once
#include<iostream>
#include<assert.h>namespace AVL
{template<class key, class value>struct TreeNode{typedef TreeNode Node;TreeNode< key, value>* left;TreeNode< key, value>* right;TreeNode< key, value>* _parent;std::pair <key, value> data;int bf;TreeNode(const std::pair<key, value>& kv = kv()):left(nullptr), right(nullptr), _parent(nullptr), data(kv), bf(0){}};template<class key, class value>class AVLTree{typedef TreeNode<key, value> Node;public:bool insert(std::pair< key, value> p){Node* cur = _root;if (cur == nullptr){_root = new Node(p);return true;}Node* parent = nullptr;while (cur){if (cur->data.first > p.first){parent = cur;cur = cur->left;}else if (cur->data.first < p.first){parent = cur;cur = cur->right;}else if (cur->data.first == p.first){return false;}}//bf 左负 右正cur = new Node(p);if (p.first < parent->data.first){parent->left = cur;}else{parent->right = cur;}cur->_parent = parent;//parent 的左右都不为空，只影响父亲//parent的左右有一个为空，影响祖先while (parent){if (cur == parent->left){parent->bf--;}else{parent->bf++;}if (parent->bf == 0){break;}else if (parent->bf == -1 || parent->bf == 1){cur = cur->_parent;parent = parent->_parent;}else if (parent->bf == -2 || parent->bf == 2)//开始旋转{if (parent->bf == 2 && cur->bf == 1)//左单旋{RotateL(parent);}else if (parent->bf == -2 && cur->bf == -1)//右单旋{RotateR(parent);}else if ((parent->bf == 2) && (cur->bf == -1))//右左双旋{RotateRL(parent);}else if ((parent->bf == -2 )&& (cur->bf == 1))//左右双旋{RotateLR(parent);}break;}}return true;}void inorder(){_inorder(_root);}void RotateL(Node* parent){Node* subR = parent->right;Node* subRL = subR->left;Node* ppNode = parent->_parent;subR->left = parent;parent->_parent = subR;parent->right = subRL;if(subRL != nullptr){subRL->_parent = parent;}if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (parent == ppNode->left){ppNode->left = subR;}else{ppNode->right = subR;}subR->_parent = ppNode;}subR->bf = 0;parent->bf = 0;}void RotateR(Node* parent){Node* subL = parent->left;Node* subLR = subL->right;Node* ppNode = parent->_parent;subL->right = parent;parent->_parent = subL;parent->left = subLR;if(subLR != nullptr){subLR->_parent = parent;}if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (parent == ppNode->left){ppNode->left = subL;}else{ppNode->right = subL;}subL->_parent = ppNode;}parent->bf = 0;subL->bf = 0;}void RotateRL(Node *parent){Node* subR = parent->right;Node* subRL = subR->left;int bf = subRL->bf;RotateR(parent->right);RotateL(parent);subRL->bf = 0;//RL的右给R的左  左子树给P的右if (bf == 1){subR->bf = 0;parent->bf = -1;}else if (bf == -1){subR->bf = 1;parent->bf = 0;}else if(bf == 0){subR->bf = 0;parent->bf = 0;}else{assert(false);}}void RotateLR(Node* parent){Node* subL = parent->left;Node* subLR = subL->right;int bf = subLR->bf;RotateL(parent->left);RotateR(parent);subLR->bf = 0;if (bf == 1){parent->bf = 0;subL->bf = -1;}else if (bf == -1){parent->bf = 1;subL->bf = 0;}else if(bf == 0){parent->bf = 0;subL->bf = 0;}else{assert(false);}}bool check(){int height = 0;return _check(_root,height);}private:Node* _root = nullptr;bool _check(Node* root,int &height){if (root == nullptr){height == 0;return true;}//检查左右子树高度差是否为1int leftheight = 0, rightheight = 0;if (!_check(root->left, leftheight) || ! _check(root->right, rightheight)){return false;}if (abs(rightheight - leftheight) >= 2){std::cout << "高度错误" << std::endl;return false;}if (rightheight - leftheight != root->bf){std::cout << "平衡因子错误" << std::endl;return false;}height = leftheight > rightheight ? leftheight+1 : rightheight+1;return true;}void _inorder(Node* root){if (root == nullptr){return;}_inorder(root->left);std::cout << "key:" << root->data.first << " " << "bf:" << root->bf << std::endl;check();			_inorder(root->right);}};}