ETLCloud介绍

ETLCloud是一款旨在解决企业数据集成挑战的最新一代平台,它集成了离线数据集成ETL、ELT、CDC实时数据集成、编排调度和数据服务API等功能,形成了一体化的DataOps数据集成平台。该平台提供私有化部署以及云原生架构,能够满足企业不同发展阶段的业务需求。此外,ETLCloud还提供开放的组件市场,使企业能够快速搭建大数据基础底座,并实现ERP、MES、OA、SaaS、API、MQ、IOT等数据的快速集成,从而构建完善的数据仓库。
数据平台集成的必要性在于整合企业内部和外部的各种数据源,实现全面的数据统一管理和分析。具体来说,数据平台集成的必要性包括以下几点:
-
提升数据价值:通过将多个数据源整合到一个平台上,可以更全面、准确地分析数据,挖掘数据背后的潜在价值,帮助企业作出更明智的决策。
-
提高工作效率:数据平台集成可以减少数据收集和整理的时间成本,让数据分析师和决策者能够更快速地获取所需数据,提高工作效率。
-
强化数据安全:通过数据平台集成,可以建立统一的数据安全管理机制,有效保护数据不被泄露或篡改,提升数据安全性。
-
促进业务创新:数据平台集成可以促进不同部门间的数据共享与交流,推动业务创新和跨部门合作,帮助企业更好地适应市场变化。
-
降低管理成本:整合多个数据源到一个平台上管理,可以降低维护和管理成本,提高资源利用率,为企业节约资金和人力成本。 综上所述,数据平台集成对企业来说至关重要,有助于提升数据价值、提高工作效率、强化数据安全、促进业务创新和降低管理成本。
通过ETLCloud演示如何集成有成财务并拉取单据数据同步
官网搜索对应组件购买安装,可以参考帮助文档的组件安装部分,这边选择有成财务的拉取单据列表组件;
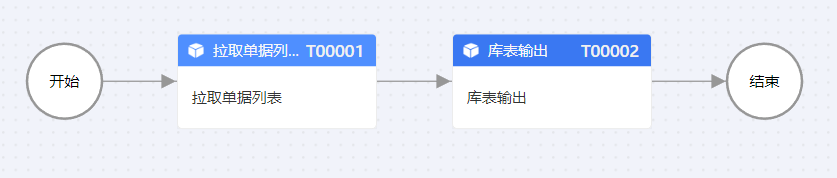
按照操作文档,安装ETL平台,运行成功后,新建离线集成流程,使用之前下载安装好的拉取单据数据组件;
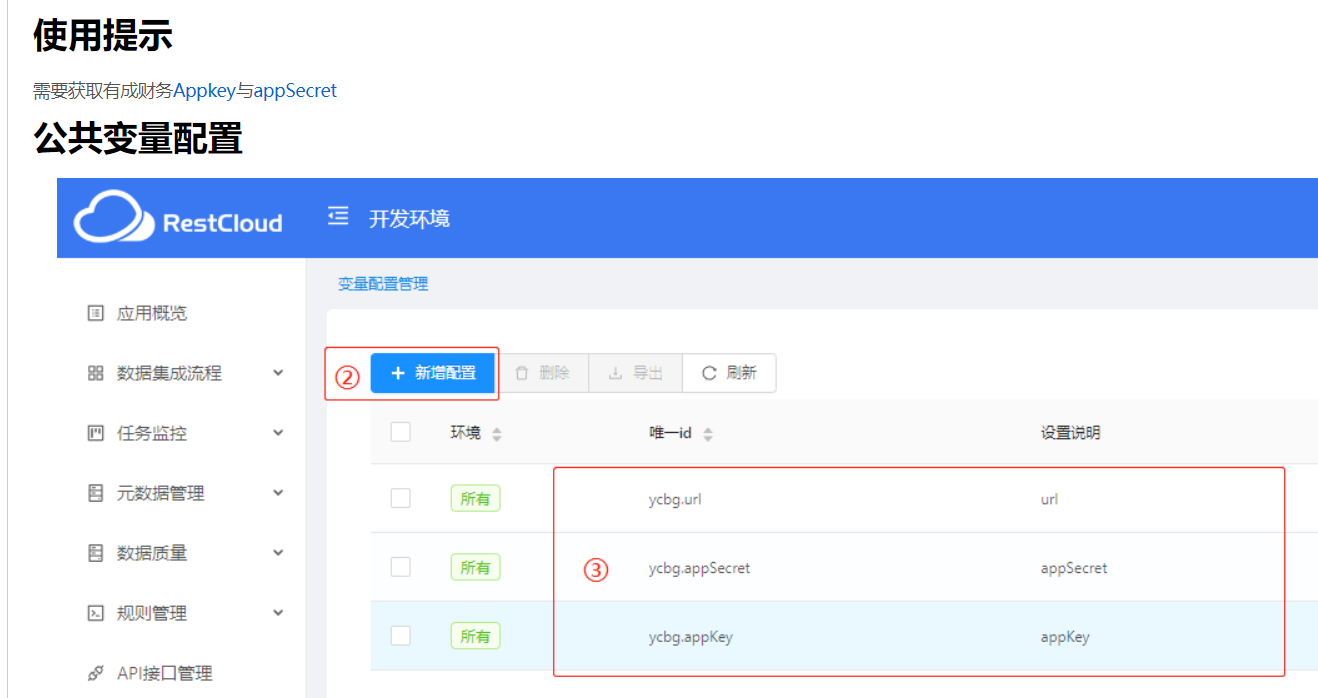
根据下载界面的组件说明来配置环境变量参数
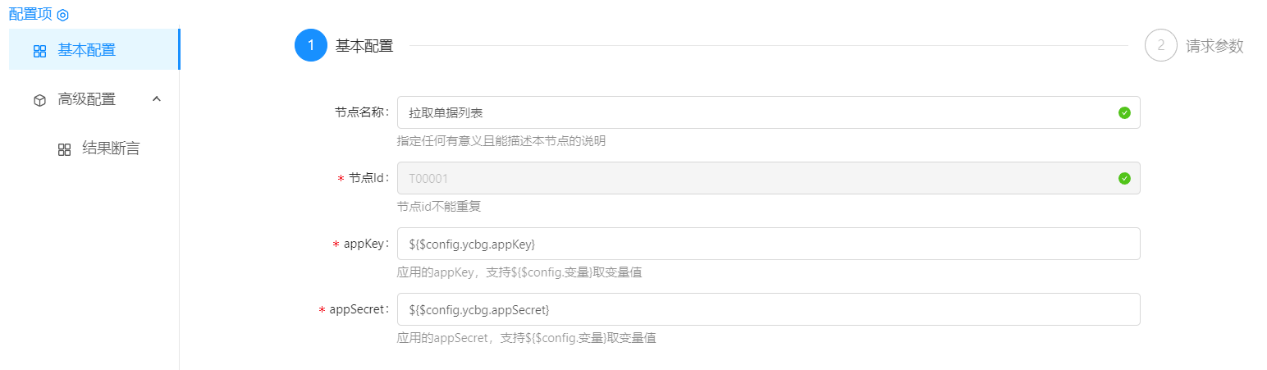
配置流程组件节点
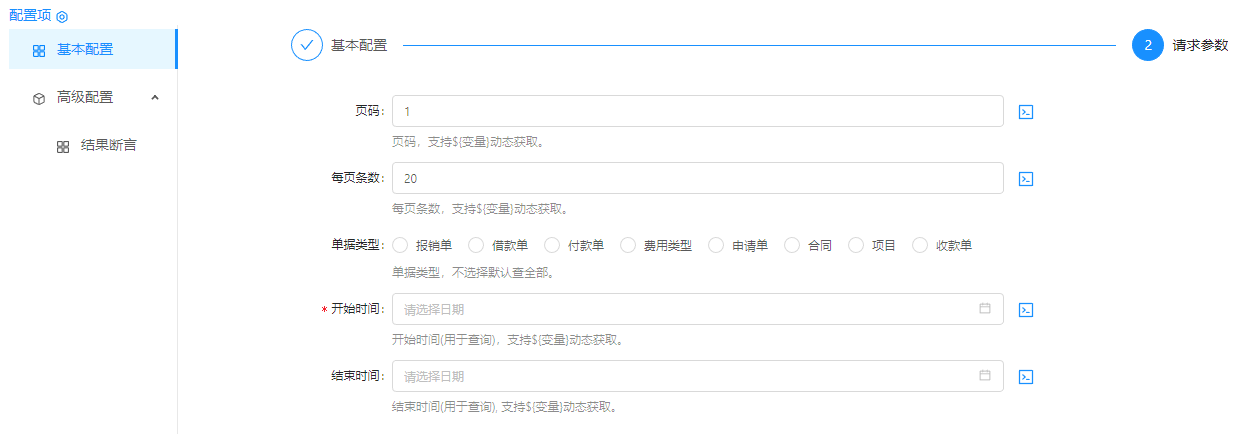
运行ETL流程后,同步到本地目标数据库后查询输出数据:

在完成上述步骤后,ETLCloud成功从有成财务系统中拉取了单据数据,并通过预配置的转换规则和清洗流程,将原始数据转化为结构化、标准化的数据格式。这一过程不仅确保了数据的质量和一致性,还大大简化了数据集成的复杂性,使得非技术人员也能方便快捷地进行数据同步操作。
借助ETLCloud企业能够高效且安全地完成跨系统的数据集成工作,有效提升数据驱动决策的能力,降低运维成本,进一步推动企业的数字化转型和业务创新。通过演示的有成财务单据数据集成案例,充分展示了ETLCloud在解决企业实际数据集成挑战方面的强大功能与灵活性。





DRF相关)






)






