在正文开始之前，我们先来聊一聊什么是集成学习？
集成学习是一种算法思想：将若干个弱学习器分组之后，产生一个新的学习器

	弱学习器指预测误差在50%以下的学习器，其中弱学习器可以是分类器、回归器弱分类器：其分类准确率仅比随机猜测的分类器好一点，因为随机猜测的准确率通常是50%（在二分类问题中）

集成学习的成功在于保证弱分类器的多样性
下面我们来介绍集成学习的三种重要思想：

• Bagging
• Boosting
• Stacking

一. Bagging思想

1. Bagging 算法

Bagging算法又称自举汇聚法

	思想：在原始数据集上通过有放回抽样(bootstrap)的方式，重新选择出S个新数据集通过训练S个新数据集得到S个分类器/回归器的集成技术处理操作：Bagging算法训练出来的模型：在分类问题中，会使用多数投票统计结果在回归问题中，会使用求均值统计结果bagging算法的弱学习器：基本的算法模型，如: Linear、Ridge、Lasso、Logistic、Softmax、ID3、C4.5、CART、SVM、KNN均可

注意：

1. bagging算法抽取出来的S个数据集是不同的，数据集内有重复样本，且重复样本各不相同；即构造了多个学习器&数据的多样性
2. bagging算法只有数据不同，弱学习器相同
3. bagging算法在抽样时，每个子集的样本数量必须和原始样本数量一致，因此抽取的子集中存在重复数据
4. bagging算法在模型训练时，允许存在重复数据

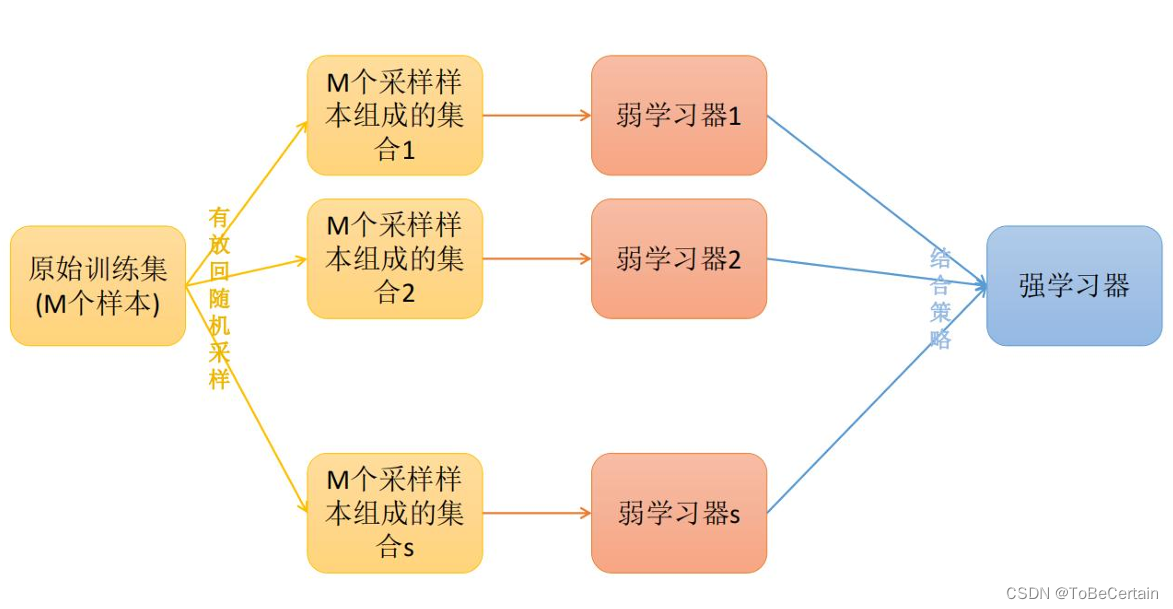
	结合策略一般为：多数投票(分类)/求均值(回归)

2. 随机森林(Random Forest)算法

随机森林算法在Bagging算法的基础上进行修改后的一种算法

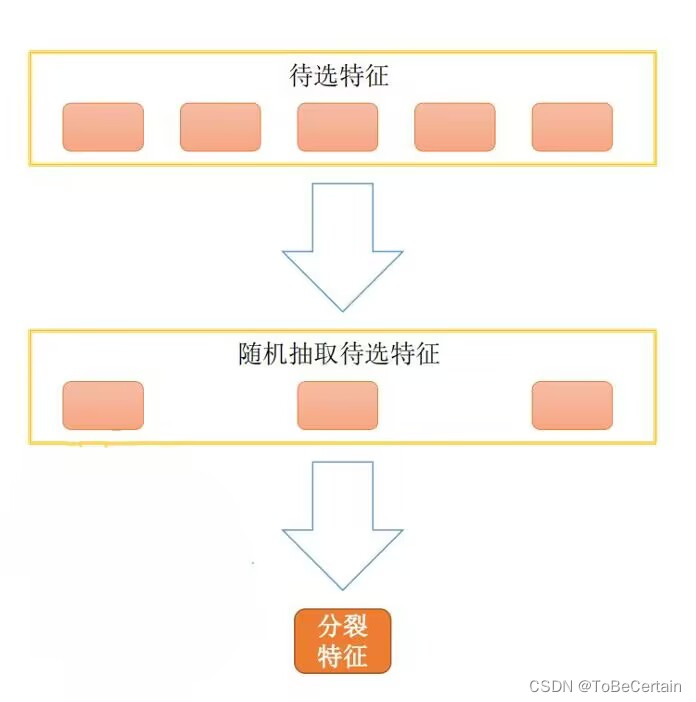
	思想：1. 在原始样本集(n个样本)上通过有放回抽样(bootstrap)的方式，选出n个样本，共m个数据集2. 将抽取出来的子数据集(存在重复数据)进行决策树训练：从抽样采集到的所有属性中，随机选择K个属性从K个属性中选择出最佳分割属性作为当前节点的划分属性按照这种方式来迭代的创建m棵决策树3. 这m个决策树形成随机森林，通过投票表决结果决定数据属于那一类处理操作：Random Forest算法在得到m个决策树形成随机森林后，通过投票表决结果/求均值决定最终数据Random Forest算法的弱学习器：一定是决策树

注意：

1. Random Forest算法抽取出来的m个数据集是不同的，每个数据集中的随机k个属性是不同的，这就导致构建的决策树也不相同；即构造了多个不同的学习器&数据的多样性
2. Random Forest算法数据不同，弱学习器构造不同
3. Random Forest算法在抽样时，每个子集的样本数量必须和原始样本数量一致，因此抽取的子集中存在重复数据
4. Random Forest算法在模型训练时，允许存在重复数据
   

---

感谢阅读🌼
如果喜欢这篇文章，记得点赞👍和转发🔄哦！
有任何想法或问题，欢迎留言交流💬，我们下次见！
本文相关代码存放位置
    【Bagging思想 代码实现】

祝愉快🌟！

---