• 三种算术表达式

  • 中缀表达式

    ((15/(7-(1+1)))*3)-(2+(1+1))

    由三个部分组成：操作数、运算符、界限符

    运算符在两个操作数中间：a+b；a+b-c；a+b-c*d

  • ❗后缀表达式 = 逆波兰表达式

    运算符在两个操作数后面：ab+；ab+c-或abc-+；ab+cd*-

  • 前缀表达式 = 波兰表达式

    运算符在两个操作数前面：+ab；-+abc；-+ab*cd

后缀表达式相关考点

中缀表达式转后缀表达式

• 中缀转后缀的方法（手算）：

  1.确定中缀表达式中各个运算符的运算顺序

  2.选择下一个运算符，按照[左操作数 右操作数 运算符]的方式合成一个新的操作数

  运算顺序不唯一，因此对应的后最表达式也不唯一

  

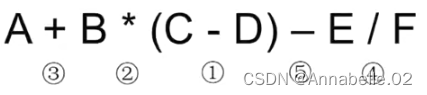
• A B C D - * + E F / -

• ---

  

  A B C D - * E F / - +

  ---

  · 这两种都是正确的，只是“机算”结果是前者

  ·🤔 “左优先”原则：只要左边的运算符能先机算，就优先算左边的

  why：确保算法的“确定性”

  3.如果还有运算符没被处理，就继续2.

• ！中缀转后缀的方法（机算，用栈实现）：

  初始化一个栈，用于保存暂时还不能确定运算顺序的运算符。

  从左到右处理各个元素，直到末尾。可能遇到三种情况：

  1. 遇到操作数。直接加入后缀表达式
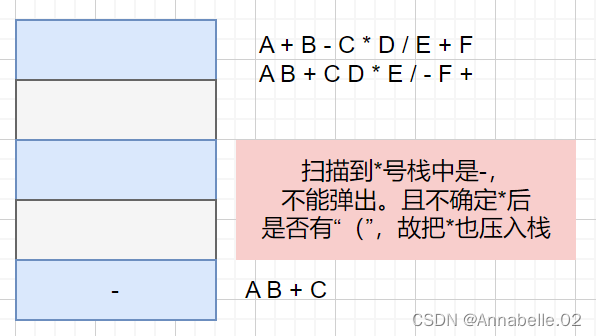
  2. 遇到界限符。遇到“（”直接入栈；遇到“）”则依次弹出站内运算符并加入后缀表达式，直到弹出“（”为止。注意：“（”不加入后缀表达式
  3. 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符，并加入后缀表达式，若碰到“（”或栈空则停止。之后再把当前运算符入栈。

  按上述方法处理完所有字符后，将栈中剩余运算符依次弹出，并加入后缀表达式。

 后缀表达式求值：

后缀表达式的手算方法：

//例子
//中缀表达式
((15/(7-(1+1)))*3)-(2+(1+1))
//后缀表达式
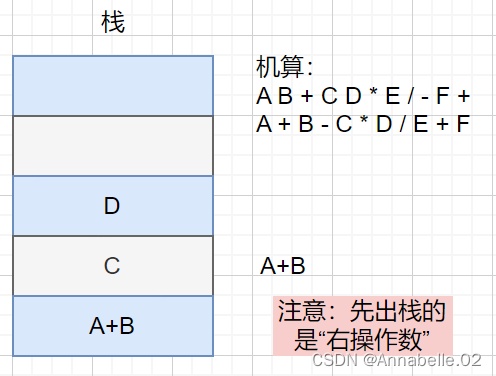
15 7 1 1 + - / 3 * 2 1 1 + + -

从左往右扫描，每遇到一个运算符，就让运算符前面最近的两个操作数执行对应运算，合体为一个操作数

👩‍💻 注意：两个操作数的左右顺序

💡 特点：最后出现的操作数先被运算 → LIFO(后进先出)栈！

• 后缀表达式的机算（机算）：

  用栈实现后缀表达式的机算：

  1. 从左到右扫描下一个元素，直到处理完所有元素
  2. 若扫描到操作数则压入栈，并回到1；否则执行3
  3. 若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到1

 👍 若表达式合法：则最后栈中只会留下一个元素，就是最终结果

• 前缀表达式相关考点

  • 中缀表达式转前缀表达式

    · [运算符 左操作数 右操作数]

    · “右优先”原则

  • 

    +A - * B - C D / E F

    · 先出栈的是“左操作数”

  • 前缀表达式求值

  💡 与中缀转后缀的内容类似

• 中缀表达式的机算（用栈实现）

  🤔 中缀转后缀+后缀表达式求值 两个算法的结合

  初始化两个栈，操作数栈和运算符栈

  若扫描到操作数，压入操作数栈

  若扫描到运算符或界限符，则按照“中缀转后缀”相同的逻辑压入运算符栈（期间也会弹出运算符，每当弹出一个运算符时，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，运算结果再压回操作数栈）