动态规划章节理论基础:
https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
01背包理论基础
链接:https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE
416. 分割等和子集
题目链接:https://leetcode.cn/problems/partition-equal-subset-sum/
思路:
动规五部曲:
(1)确定dp数组以及下标含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
拿输入数组 [1, 5, 11, 5],举例, dp[7] 只能等于 6,因为 只能放进 1 和 5。
而dp[6] 就可以等于6了,放进1 和 5,那么dp[6] == 6,说明背包装满了。
(2)确定递归公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
(3)dp数组初始化
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
本题题目中 只包含正整数的非空数组,所以非0下标的元素初始化为0就可以了。
(4)确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
(5)举例推导dp数组
dp[j]的数值一定是小于等于j的。
如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j,理解这一点很重要。
用例1,输入[1,5,11,5] 为例,如图:
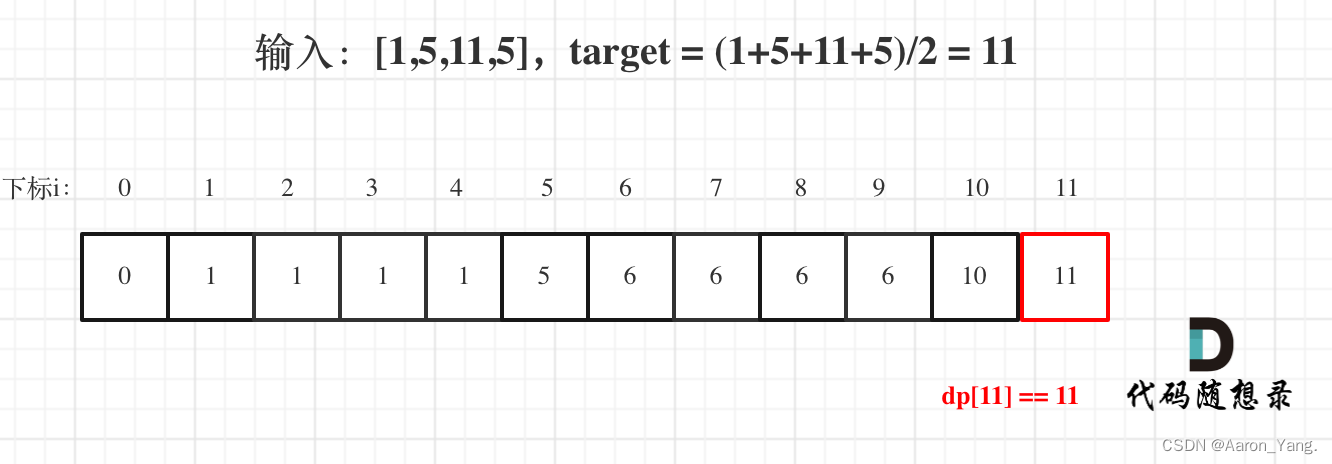
最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
代码:
class Solution {public boolean canPartition(int[] nums) {int sum = 0;for(int i:nums)sum += i;// 奇数不能平分if(sum % 2 == 1) return false;int target = sum >> 1;int[] dp = new int[target+1];for(int i=0 ; i< nums.length ; i++){for(int j=target ; j>= nums[i] ;j--){dp[j] = Math.max(dp[j],dp[j-nums[i]]+ nums[i]);}// 剪枝if(dp[target] == target) return true;}return dp[target] == target;}
}





)
|基本语法概述)




)


的人面定位算法,Matlab实现)
)



