久违的没做太出来的题目，leetcod 685. 冗余连接 II
题目
在本问题中，有根树指满足以下条件的 有向 图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。
输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。
返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。
示例 1：
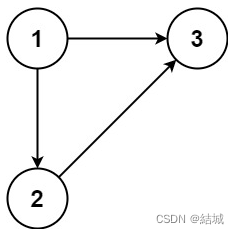
输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]
示例 2：
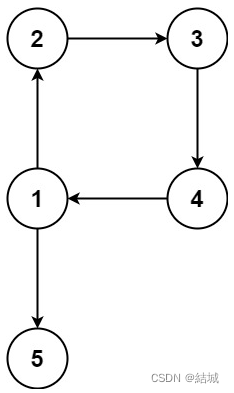
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]
提示：
n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ui, vi <= n
思路
本来还想直接像684一样直接并查集查到属于同一个祖先下的就返回直接ac了。没想到给我上了一课。事实上，这道题一共分三种情况讨论：
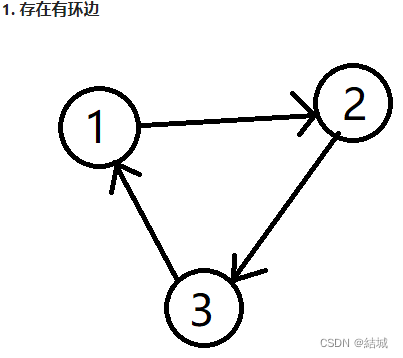
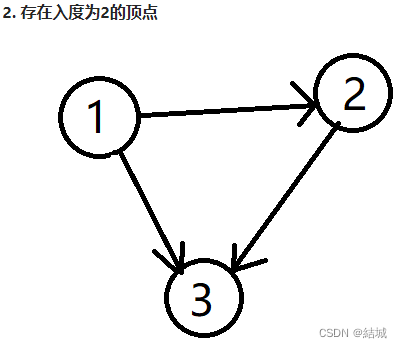
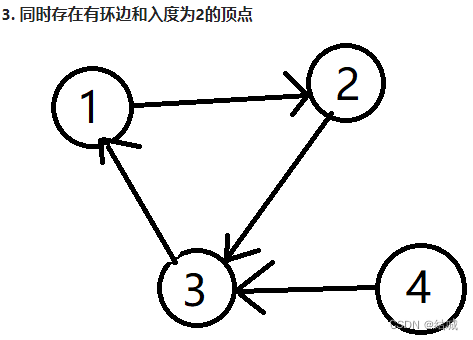
题解
class Solution {int[] p;int n;public int[] findRedundantDirectedConnection(int[][] edges) {n = edges.length;int[] inDegree = new int[n+1];int node = -1;// 记录有没有入度为2的节点for (int i=0;i<n;i++) {if (++inDegree[edges[i][1]] > 1) {node = edges[i][1];}}// 如果有入度为2的节点，就倒着找这个入度为2的节点的入度连接去删除，看看是不是一个树if (node > -1) {for (int i=n-1;i>=0;i--) {if (edges[i][1] == node) {if (check(edges, edges[i])) {return edges[i];}}}}// 如果没有入度为2的树那就是图里有环了，删除最后一个出现的就可以破坏环p = new int[n+1];for (int i=1;i<=n;i++) {p[i] = i;}for (int i=0;i<n;i++) {int a = edges[i][0], b = edges[i][1];int pa = find(a), pb = find(b);if (pa != pb) {p[pa] = pb;}else {return edges[i];}}return null;}public int find(int x) {if (p[x] != x) {p[x] = find(p[x]);}return p[x];}public boolean check(int[][] edges, int[] edge) {p = new int[n+1];for (int i=1;i<=n;i++) {p[i] = i;}for (int i=0;i<n;i++) {if (Arrays.equals(edge, edges[i])) {continue;}int a = edges[i][0], b = edges[i][1];int pa = find(a), pb = find(b);if (pa != pb) {p[pa] = pb;}else {return false;}}return true;}
}
