软考77-上午题-【面向对象技术3-设计模式】-创建型设计模式02

一、生成器模式

1-1、意图

将一个复杂对象的构建与它的表示分离，使得同样的构建过程可以创建不同的表示。

1-2、结构图

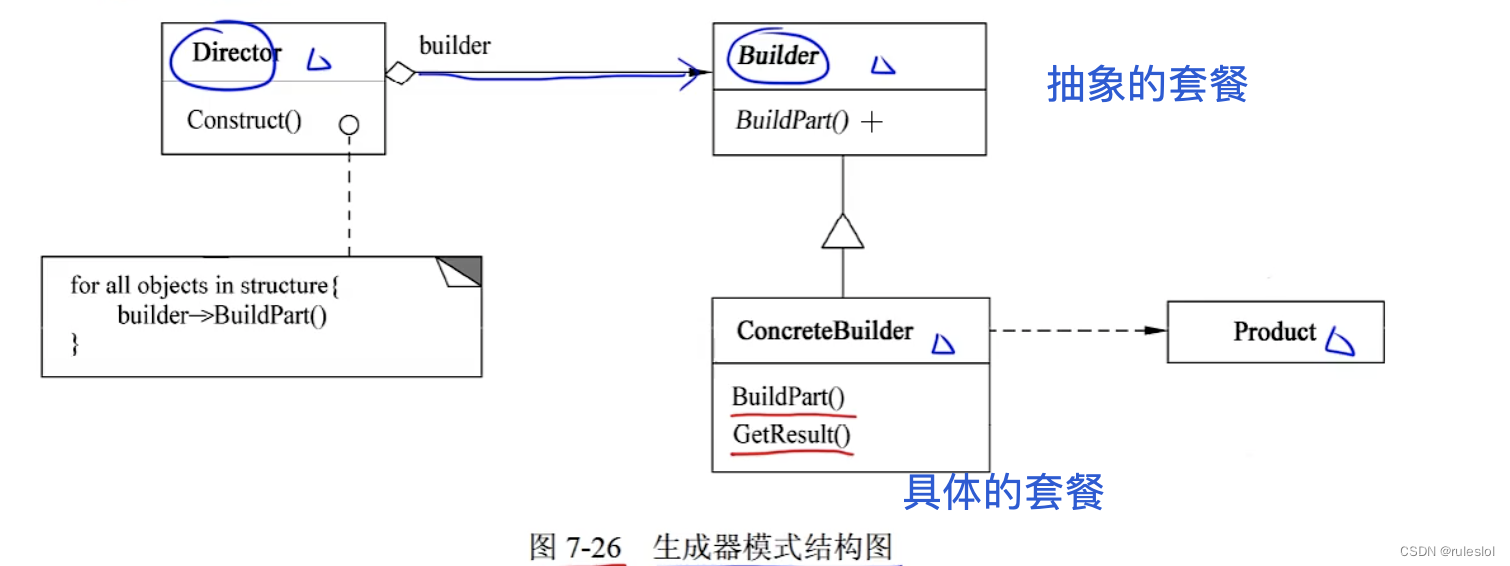
Builder 为创建一个 Product 对象的各个部件指定抽象接口。
ConcreteBuilder 实现 Builder 的接口以构造和装配该产品的各个部件，定义并明确它所创建的表示，提供一个检索产品的接口。
Director 构造一个使用 Builder 接口的对象。
Product 表示被构造的复杂对象。
ConcreteBuilder 创建该产品的内部表示并定义它的装配过程。包含定义组成组件的类，包括将这些组件装配成最终产品的接口。

1-3、代码表示

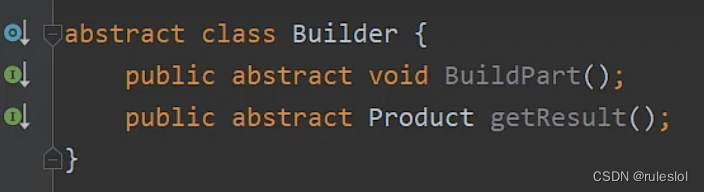
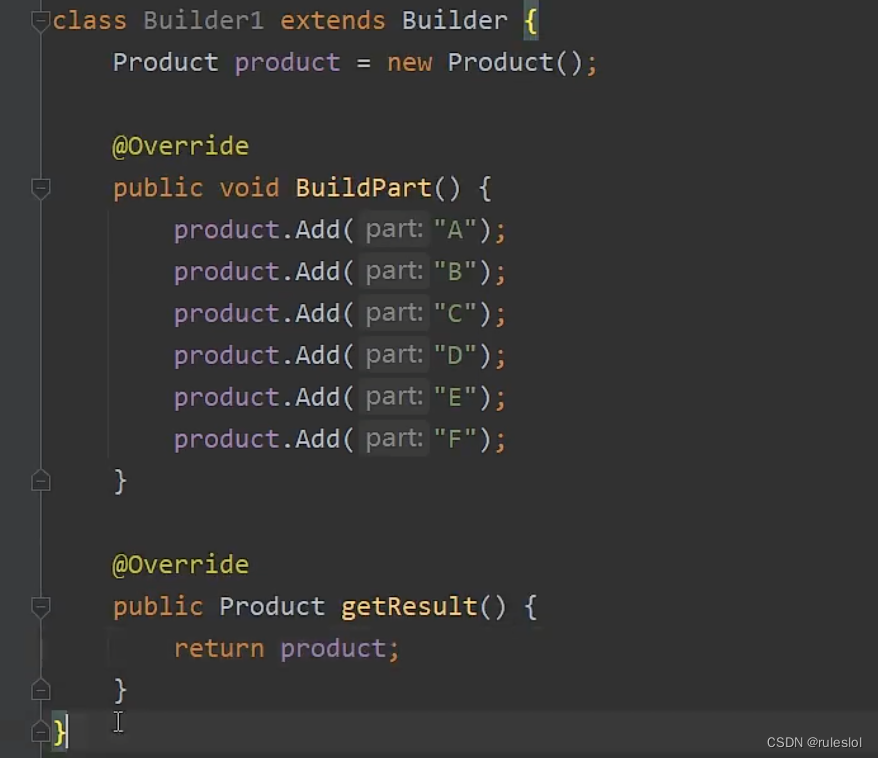
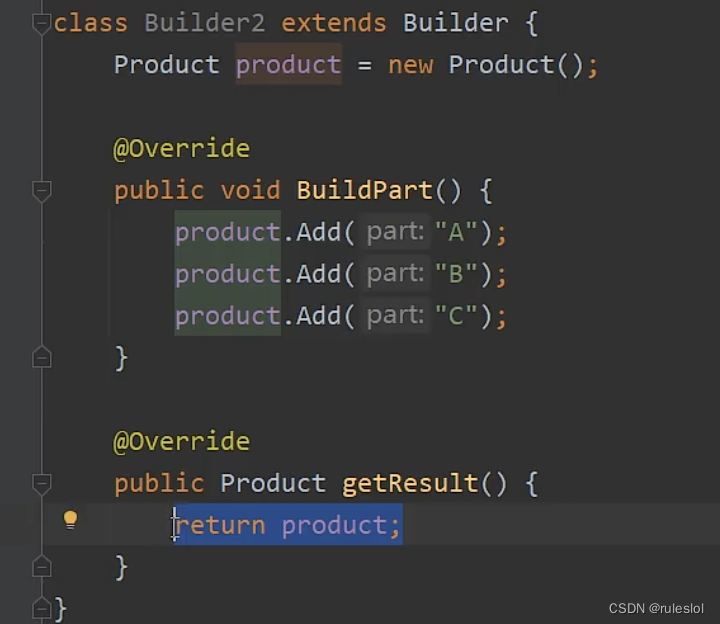
1-4、适用性

当创建复杂对象的算法应该独立于该对象的组成部分以及它们的装配方式时。

当构造过程必须允许被构造的对象有不同的表示时。

1-5、真题

真题1：

真题2：

真题3：

二、原型模式

上午题没怎么考过，考下午题。

2-1、意图

用原型实例指定创建对象的种类，并且通过复制这些原型创建新的对象。

2-2、结构图

Prototype 声明一个复制自身的接口。
ConcretePrototype 实现一个复制自身的操作。
Client 让一个原型复制自身从而创建一个新的对象。

2-3、代码表示

抽象原型：

interface ProtoType {public Object Clone();
}

具体原型：

package Design23;public class Product implements ProtoType{private int id;private double price;public Product(){}public Product(int id, double price){this.id = id;this.price = price;}public int getId() {return id;}public double getPrice() {return price;}@Overridepublic Object Clone() {Product product = new Product();product.id = this.id;product.price = this.price;return product;}
}

客户端：

java中已经提供了一个克隆的接口：

package Design23;public class Product implements Cloneable{private int id;private double price;public Product(){}public Product(int id, double price){this.id = id;this.price = price;}public int getId() {return id;}public double getPrice() {return price;}@Overridepublic Object clone() throws CloneNotSupportedException {return super.clone();}
}

2-4、适用性

当一个系统应该独立于它的产品创建、构成和表示时。
当要实例化的类是在运行时刻指定时，例如，通过动态装载。
为了避免创建一个与产品类层次平行的工厂类层次时。
当一个类的实例只能有几个不同状态组合中的一种时。建立相应数目的原型并克隆它们，可能比每次用合适的状态手工实例化该类更方便一些。

三、单例模式

只考上午题。

3-1、意图

保证一个类仅有一个实例，并提供一个访问它的全局访问点。

3-2、结构图

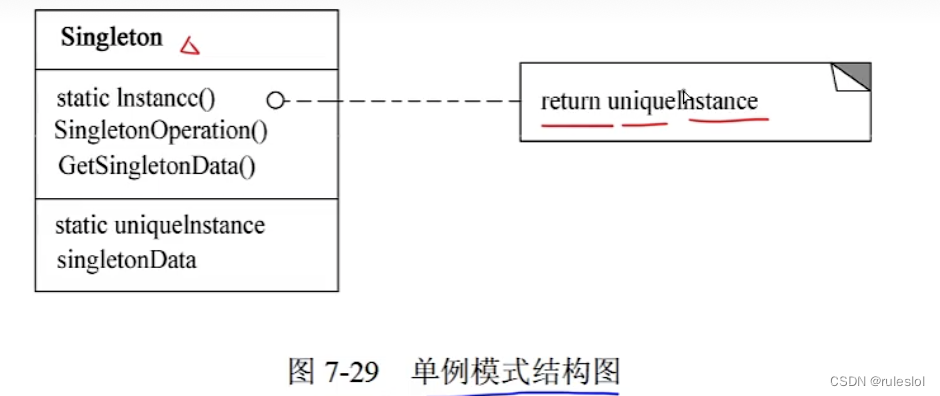
3-3、代码实现

package Design23;public class Singleton {private int number = 2024;public int getNumber() {return number;}public void setNumber(int number) {this.number = number;}// 创建一个唯一的实例static Singleton instance = new Singleton();// public Singleton(){}private Singleton(){}// 访问它的全局访问点public static Singleton getInstance(){return instance;}}

public class SingletonMain {public static void main(String[] args) {Singleton singleton1 = Singleton.getInstance();Singleton singleton2 = Singleton.getInstance();System.out.println(singleton1.getNumber() + " " + singleton2.getNumber());singleton1.setNumber(22);System.out.println(singleton1.getNumber() + " " + singleton2.getNumber());}}