堆的概念
1.堆是一个完全二叉树
2.小堆(任何一个父亲<=孩子),大堆(任何一个父亲>=孩子)
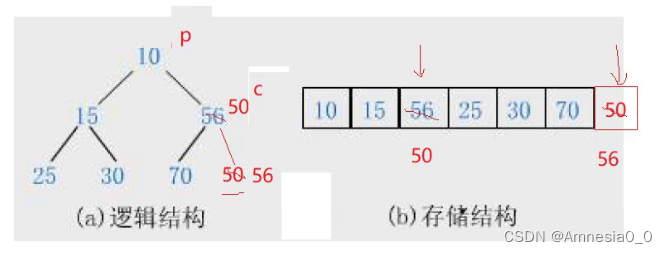
堆的结构
物理结构:数组
逻辑结构:二叉树
#pragma once
#include<assert.h>
#include<iostream>
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;// 堆的构建
void HeapInit(Heap* hp);
void HeapInitArray(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);
#include"标头.h"
void HeapInit(Heap* hp)
{assert(hp);hp->_a = NULL;hp->_capacity = 0;hp->_size = 0;
}void HeapInitArray(Heap* hp, HPDataType* a, int n)// 一次性初始化堆,插入所有值
{assert(hp);hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * n);memcpy(hp->_a, a, sizeof(HPDataType) * n);
//第一个节点不用调,时间复杂度为O(n*logn)//for (int i = 1; i < n; i++)//向上调整建堆//{// AdjustUp(hp->_a, i);//}
//叶节点不用调(没有子节点),时间复杂度为O(N)for (int i = (hp->_size-1 - 1) / 2; i >= 0; i--)//向下调整建堆//(hp->_size-1 - 1) / 2第一个-1是下标,后面的-1和/2是求父节点的公式{AdjustDown(hp->_a, hp->_size, i);}
}void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = 0;hp->_size = 0;
}void Swap(HPDataType* px, HPDataType* py)
{HPDataType temp = *px;*px = *py;*py = temp;
}
void AdjustUp(HPDataType* a, int child)//向上调整数据,是它成小堆/大堆
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_size == hp->_capacity){size_t newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;HPDataType* temp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);if (temp == NULL){perror("realloc fail");return;}hp->_a = temp;hp->_capacity = newcapacity;}hp->_a[hp->_size] = x;hp->_size++;AdjustUp(hp->_a, hp->_size - 1);
}void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//假设法选出小的孩子while (child < n){if (a[child + 1] < a[child] && child + 1 < n){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void HeapPop(Heap* hp)//删除堆顶的数据
{assert(hp);assert(hp->_size > 0);//不可以挪动覆盖来删除堆顶数据//问题1.挪动覆盖时间复杂度O(N)// 2.堆结构被破坏,父子变兄弟,兄弟变父子//因此可以将首尾数据交换,删除尾部数据,然后进行向下调整算法Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;AdjustDown(hp->_a, hp->_size, 0);
}HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->_a[0];
}int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}bool HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}堆排序
堆排序的本质是利用堆的性质,取出堆顶的数(最大或最小),然后将堆顶换成第二小/大的数
void HpSort(HPDataType* a, int n)
{Heap hp;HeapInitArray(&hp, a, n);int i = 0;while (!HeapEmpty(&hp)){a[i++] = HeapTop(&hp);HeapPop(&hp);}HeapDestory(&hp);
}当然,这样的排序存在一定的缺点:
1.空间复杂度为O(N),太大了
2.使用是需要有堆这个数据结构
为了节省空间,可以通过将原数组改造成堆来排序,
排列出升序的数组采取堆排序应当使用大堆,因为小堆的堆顶是最小的数,堆顶的数已经是最小的了,不能改了
因此需要其他的数重新组成一个新堆,但是原本的堆全部乱了,父子变兄弟等问题会出现,只能重新建堆,浪费了时间因此需要采用大堆
大堆的堆顶是最大的,因此可以进行首尾交换,最大值就在数组尾部了,然后不把最后一个数看作堆内的数,继续进行向下调整,就可以选出次大的数
//创建大堆的向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//假设法选出小的孩子while (child < n){if (a[child + 1] > a[child] && child + 1 < n){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void HpSort(HPDataType* a, int n)
{//先将数组建堆,时间复杂度O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i)//调整叶子上一层(叶子(最后面)在最后,不需要调整){AdjustDown(a, n, i);}//int end = n - 1;//end为数组下标while (end > 0){Swap(&a[0], &a[end]);//交换首尾AdjustDown(a, end, 0);//将堆首下调--end;}
}int main()
{int a[9] = { 9,8,7,6,5,4,3,2,1 };HeapSort(a, 9);for (int i = 0; i < 9; i++){printf("%d ", a[i]);}return 0;
}
这样,一个简单的堆排序就完成了




详解)



)



 - SignalTrack信号轨道和自定义带参数的Marker信号和轨道)






