最近在看Gemma代码感觉比LLama的代码看的方便点， 看到RoPE代码跟常规的方式不太一样（也不算常规，就是我理解的方式），特此记录一下。我的RoPE入门代码参考：Rotary Position Embedding (RoPE, 旋转式位置编码) | 原理讲解+torch代码实现
原理我就不讲了，直接贴一下图，图源自于上面的链接。
我们先粘贴一下代码，逐步讲解：
dim:单头维度信息
end:序列长度
theta:10000
def precompute_freqs_cis(dim: int,end: int,theta: float = 10000.0) -> torch.Tensor:"""Precomputes the frequency cis."""freqs = 1.0 / (theta**(torch.arange(0, dim, 2)[:(dim // 2)].float() / dim))t = torch.arange(end, device=freqs.device)freqs = torch.outer(t, freqs).float()freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64return freqs_cisx:输入特征维度[batch, end, num_head, dim]
freqs_cis:上个函数获取的结果
def apply_rotary_emb(x: torch.Tensor, freqs_cis: torch.Tensor) -> torch.Tensor:"""Applies the rotary embedding to the query and key tensors."""x_ = torch.view_as_complex(torch.stack(torch.chunk(x.transpose(1, 2).float(), 2, dim=-1),dim=-1))x_out = torch.view_as_real(x_ * freqs_cis).type_as(x)x_out = torch.cat(torch.chunk(x_out, 2, dim=-1), dim=-2)x_out = x_out.reshape(x_out.shape[0], x_out.shape[1], x_out.shape[2],-1).transpose(1, 2)return x_out
precompute_freqs_cis
- freqs = 1.0 / (theta**(torch.arange(0, dim, 2)[:(dim // 2)].float() / dim))
这个代码主要是实现一下公式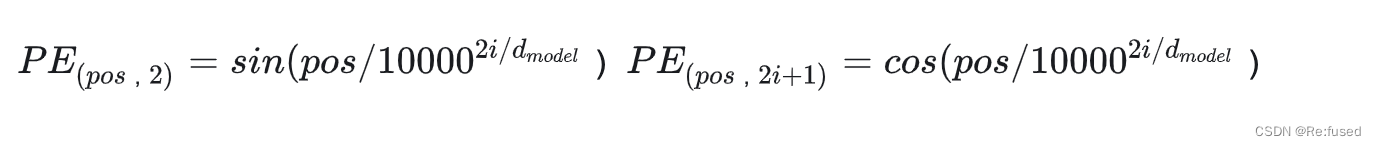
torch.arange(0, dim, 2),生成列表 [0,2, …d_model//2] - t = torch.arange(end, device=freqs.device)
生成序列长度， [0, 1, …, end(也就是序列长度)] - freqs = torch.outer(t, freqs).float()
进行笛卡尔积，维度变成[end, dim//2]
- freqs_cis = torch.polar(torch.ones_like(freqs), freqs)
通过polar函数生成cos和sin值，为什么要使用torch.ones_like(freqs)， 下面公式，abs为1，不就是cos值和sin值了
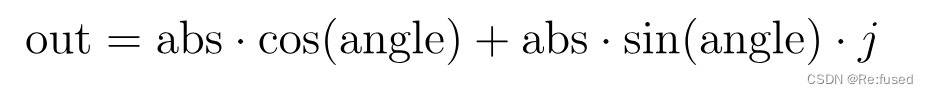
apply_rotary_emb
- x_ = torch.view_as_complex(
torch.stack(torch.chunk(x.transpose(1, 2).float(), 2, dim=-1),
dim=-1))
x.transpose(1, 2).float()将输入维度变为[batch, num_head, end, dim]
torch.chunk将数据前dim//2 和后dim//2分开，我理解的是[q0, q1, …qn]是奇偶分开，而不是前后分开，可能无所谓吧。
torch.stack则是对维度进行合并，产生[batch, num_head, end, dim//2, 2]这种维度。
我简单举例子验证一下：
import torch
a = torch.arange(10)
print(a)
b = torch.chunk(a, 2, dim=-1)
print(b)
c = torch.stack(b, dim = -1)
print(c)
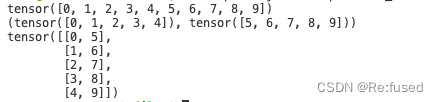
并且用torch.view_as_complex转为复述的形式
- x_out = torch.view_as_real(x_ * freqs_cis).type_as(x)
x_ * freqs_cis实现复述的预算
举例子解释一下：
x_为：q0+q1 i
freqs_cis:cos+sin i
实部为：q0cos -q1sin
虚部为：q1cos + q1sin
torch.view_as_real函数则是把转为实数的形式，a+bi->[a, b]形式 - x_out = torch.cat(torch.chunk(x_out, 2, dim=-1), dim=-2)
则是把维度转为[batch, num_head, end, dim]的形式 - x_out = x_out.reshape(x_out.shape[0], x_out.shape[1], x_out.shape[2],
-1).transpose(1, 2)
转为输入的形式
下面为LLama的RoPE实现：
def apply_rotary_emb(xq: torch.Tensor,xk: torch.Tensor,freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))freqs_cis = reshape_for_broadcast(freqs_cis, xq_)xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)return xq_out.type_as(xq), xk_out.type_as(xk)
LLama我理解，他则是采用类似于奇偶分开的方式，我简单尝试了一下：
import torch
a = torch.arange(10)
print(a)
b = a.reshape(5,2)
print(b)
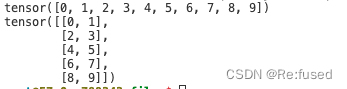
总结：
以上就是我对RoPE代码实现的理解，相比原来理解的方式，这种相对更加简洁，但是略有一些绕
