GSC（generalized sidelobe canceller, 广义旁瓣消除器）可以将有约束的LCMV算法转换为无约束的实现结构。网上关于GSC的介绍对细节方面介绍得不详细，并且主要是应用在窄带。宽带的GSC应用范围也比较广泛，例如在智能音箱等产品的麦克风阵列信号处理中，GSC作为核心算法。本文介绍了GSC的结构以及相关的公式推导，主要关注时域宽带GSC的实现，并给出了python的实现代码示例。关于波束形成基础知识，请参考宽带波束形成，窄带波束形成

GSC的结构

将有约束的LCMV（线性约束最小方差） 波束形成器转换为无约束的GSC结构，如下图所示

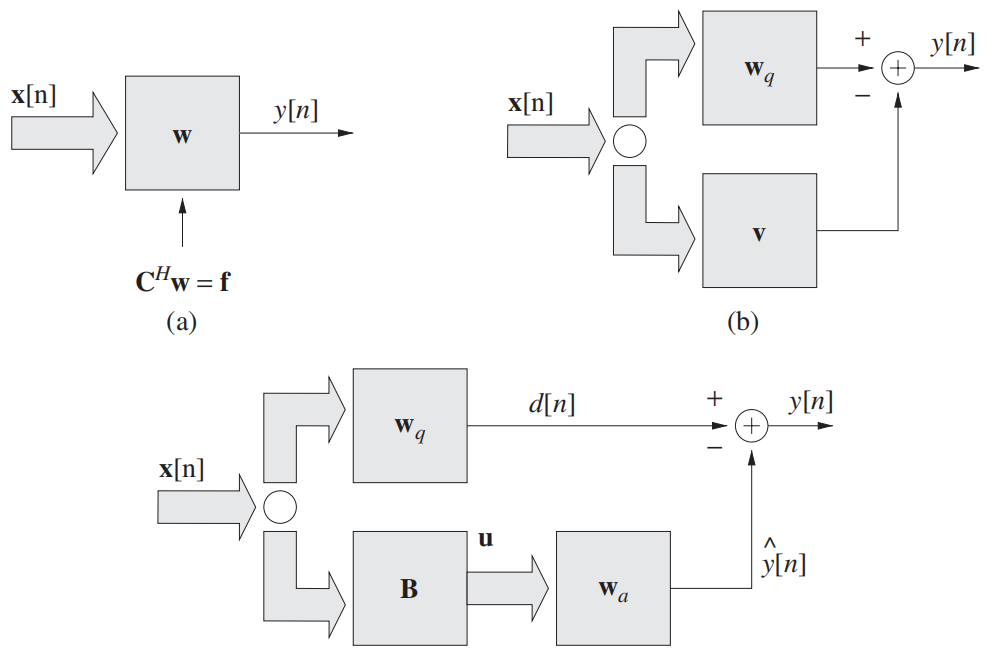
(a) 有约束的LCMV波束形成器

(b) 将权重向量分解为两个正交的成分和，即，，

(c) 进一步将补空间分解为自适应部分和固定部分，从而得到无约束自适应问题

上面是对通过伪逆的方法求的解。

定义（矩阵的秩，线性独立的部分），因为向量位于的补空间，所以阻塞矩阵有列，行

可以通过正交方法例如QR分解从中获取。还可以通过CCD方法以及SVD分解方法，我们在后面的博客文章中介绍。

上图的GSC是时域的处理结构，输入是n时刻的，的表达式请参考上一篇博客：宽带波束形成

的是长度为的列向量。

python的宽带（如麦克风阵列信号处理）GSC实现代码

import numpy as npmatrices = (C,fr,Bk) # C,fr,Bk是固定的矩阵系数，计算方法下一篇博客会讲到coeficientes = np.dot(matrices[0],np.dot(np.linalg.inv(np.dot(matrices[0].T, matrices[0])),matrices[1])) # wq
w_adp = np.zeros(Bk.shape[1])muu = 2e-10 # LMS步长
err = np.zeros(M_Sigs.shape[1])
Xd = np.zeros((M,J))
M_S = np.concatenate((M_Sigs[:,::-1],Xd),axis=1)
for i in range(1,M_S.shape[-1]-J):Xmj = M_S[:,-i-J:-i].T.flatten()out_up = np.dot(coeficientes,Xmj) # 固定滤波x_u = np.dot(matrices[2].T,Xmj) # 经过阻塞矩阵err[i] = out_up - np.dot(x_u,w_adp) # 计算输出（误差信号）w_adp += muu*err[i]*x_u # 更新自适应滤波器的权重

后面会进一步介绍GSC的加速算法，如子带GSC，PBFDAF GSC等等。