参加了大大小小很多场比赛了，但是都是混子，但还是打算记录一下吧，系统认真过一遍。后续功力深厚，会拓展写的文章，目前是干货，一些背景啥的还都未介绍。

1.介绍

随机抽样，求取近似解。
当无法求得精确解时，进行随机抽样，根据统计试验求近似解，
我的理解就是从一个样本抽取一些数据，进而估计整体的解，由于是抽取的样本数据，因此是近似解。
样本越大，越接近真实值，也就是数学统计值，

！！！注意：蒙特卡洛法是个思路，不是算法，具体问题具体分析。

2.可以做的题型

概率模型：蒙特卡洛算法可以用于模拟复杂的概率模型。例如，在金融领域中，可以使用蒙特卡洛方法来模拟股票价格的随机演化，并进行风险估计和投资组合优化。
最优化问题：蒙特卡洛算法可以用于求解最优化问题。例如，在运筹学中，可以使用蒙特卡洛方法来求解旅行商问题、装箱问题等。
数值计算：蒙特卡洛算法在数值计算中很有用。例如，在微分方程的数值求解中，可以使用蒙特卡洛方法来模拟随机扰动，从而获得系统的稳定解。
随机模型：蒙特卡洛算法可以用于研究随机模型的性质和行为。例如，在生物学中，可以使用蒙特卡洛方法来模拟基因演化和遗传算法。
不确定性分析：蒙特卡洛算法可以用于分析模型的不确定性。例如，在环境科学中，可以使用蒙特卡洛方法来进行不确定性分析和灾害模拟。
等等。

3.实战

3.1求pi的值

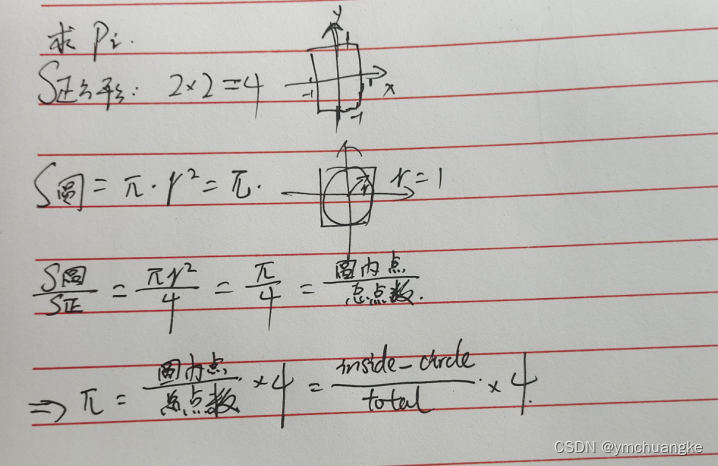
import random #导入random生成随机数#d定义一个估计pi的函数，传入形参num_saamples
def estimate_pi(num_samples):# 定义变量inside_circle = 0  #园内点数total = 0  #总点数#定义for循环，下划线表示在循环中未使用这个变量的值#正常for应该是for 变量 in xxx（范围）：for _ in range(num_samples):#定义xy坐标，正方形面积为2*2=4x = random.uniform(-1, 1) #random随机函数y = random.uniform(-1, 1)#求距离distance = x ** 2 + y ** 2#判断if distance <= 1: #园内点inside_circle += 1 #园内加一total += 1 #循环一次，总点数加一pi_estimate = 4 * inside_circle / total #pi的估计值return pi_estimate  #这个函数返回的是pi的估计值num_samples = 100000 #定义循环次数
pi = estimate_pi(num_samples) #求pi的估计值
print("Estimated value of pi:", pi) #打印pi的估计值

3.2求定积分x^2 的值

import random #导入randomdef monte_carlo_integration(func, a, b, num_samples): #定义求取定积分的函数，传入形参func，a，b，numsamplestotal = 0.0 #定义浮点型变量for _ in range(num_samples):# 定义一个循环，只需要循环，不需要值，用c的话相当于#for(int i=0;i<=inum_samples;i++;)x = random.uniform(a, b) #产生一个【0，1】的数total += func(x)  #算函数值累计求和average = total / num_samples #求平均integral = average * (b - a) #算面积（积分值）return integral #返回积分值def f(x): #定义一个函数，返回x^2的值return x**2a = 0
b = 1
num_samples = 100000integral = monte_carlo_integration(f, a, b, num_samples) #形参传入函数的名字，a,b，num_samples
print("The integral of f(x) = x^2 from", a, "to", b, "is approximately:", integral)