小波分析是较好的非平稳信号分析方法之一，它通过伸缩和平移运算对信号进行多尺度细化分析，能够在不同的尺度上描述信号的局部特征，为微弱故障特征信号的检测提供了有效的工具。小波尺度谱可看作一个有恒定相对带宽的谱图，能够反映信号的时频信息，广泛应用于非平稳信号分析。
信号的连续小波变换对时间不敏感而对尺度敏感，在信号的小波变换尺度域实际上对应了信号的频率，并且信号的能量在不同的运行模式与不同的频率处是不同的。所以，可以将信号转化为对尺度的表示，提取信号在各尺度下的能量或与能量相对应的值作为特征信息。的时间平均小波谱反映了小波功率谱沿尺度方向的分布情况，尺度间隔选的足够小，即可达到比较精细的尺度分割。
Morlet 小波是由Gauss函数调制的连续性平面波，在时频两域都具有很好的局部性，其函数表达式为：
采用Morlet小波方法进行时间序列的周期性分析用于样本长度的计算。考虑到实际应用，再结合移动窗方法完成样本提取的同时，提升数据利用率，实现数据扩充。
该程序绘制一维时间序列信号的小波尺度谱和时间平均小波谱，基于Morlet小波，运行环境为Python，部分代码如下：
import scipy.io as load
Signal = load.loadmat('SCGwithResp.mat')
resp = Signal['resp'].ravel()
scg = Signal['scg'].ravel()
from scipy import signal
resp = signal.resample(resp, int(len(resp)*5/100))
scg = signal.resample(scg, int(len(scg)*5/100))
部分出图如下·：
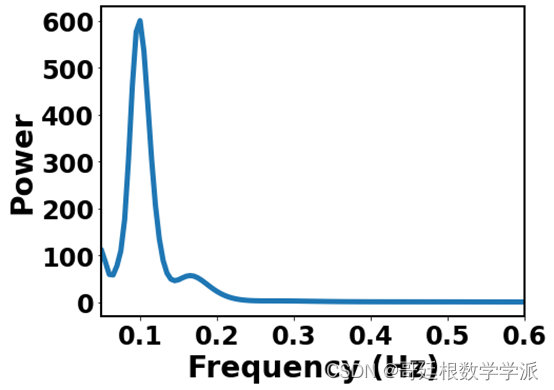
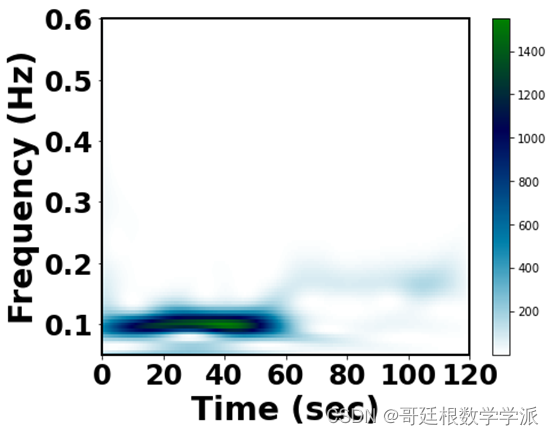
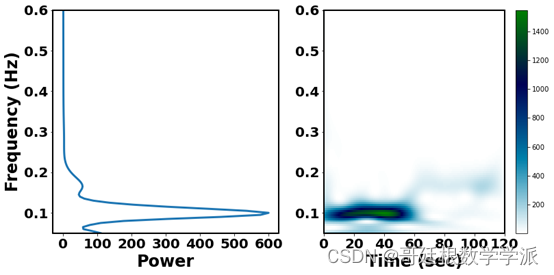
完整代码：Python环境下一维时间序列的小波尺度谱和时间平均小波谱（基于Morlet小波）
工学博士，担任《Mechanical System and Signal Processing》审稿专家，担任《中国电机工程学报》优秀审稿专家，《控制与决策》，《系统工程与电子技术》，《电力系统保护与控制》，《宇航学报》等EI期刊审稿专家。
擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
