第五题:T5推箱子
标签:排序、数学、思维
题意:给定 t t t组数据,每组数据给定长度为 n n n的字符串, @ @ @表示箱子, _ \_ _表示空格,求把箱子都推到一起(即两两箱子之间没有空格),最少移动次数。
题解:我们稍微把题意变下,给定 n n n个点在 x x x轴上的的坐标,求把这些点移到同一个位置的最少移动次数。
举个例子(坐标): 3 5 8 10 3 \ 5 \ 8 \ 10 3 5 8 10
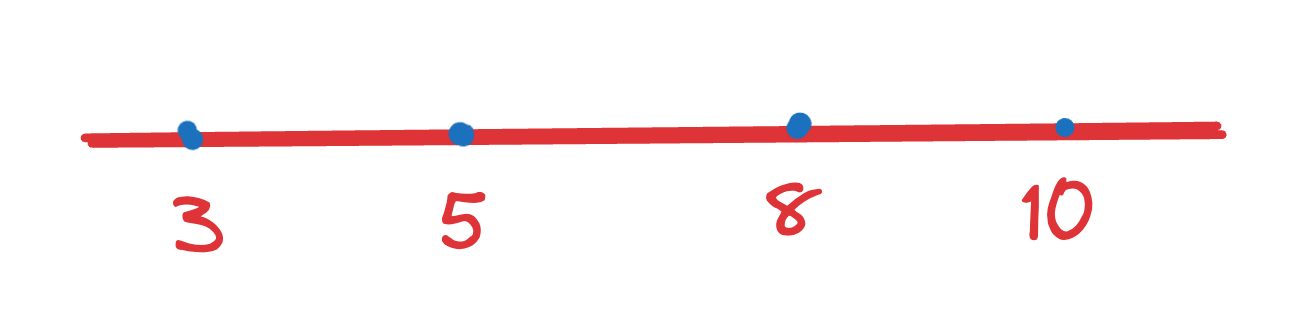
如果把这些点都移到 2 2 2的坐标,移动次数为: 1 + 3 + 6 + 8 = 18 1+3+6+8=18 1+3+6+8=18
如果把这些点都移到 3 3 3的坐标,移动次数为: 0 + 2 + 5 + 7 = 14 0+2+5+7=14 0+2+5+7=14
如果把这些点都移到 5 5 5的坐标,移动次数为: 2 + 0 + 3 + 5 = 10 2+0+3+5=10 2+0+3+5=10
如果把这些点都移到 6 6 6的坐标,移动次数为: 3 + 1 + 2 + 4 = 10 3+1+2+4=10 3+1+2+4=10
如果把这些点都移到 8 8 8的坐标,移动次数为: 5 + 3 + 0 + 2 = 10 5+3+0+2=10 5+3+0+2=10
会发现把点移到这些点中最中间那个点,移动次数最少,推箱子问题同理,只不过得去考虑每个箱子会占一个位置,在中间位置( k k k)左边的第一个箱子推到 k − 1 k-1 k−1的位置,其他的同理,即对于第 i i i 个箱子来说,需要移动的距离为 a[k] - a[i] - (k-i)(i<k);在中间位置右边的第 i i i个箱子,同理,需要移动的距离为 a[i] - a[k] - (i-k)(i>k)。
代码:
#include <bits/stdc++.h>
using namespace std;typedef long long ll;
string s;
ll a[1000005];int main() {ll t, n;cin >> t;while (t--) {cin >> n >> s;ll c = 0, ans = 0;for (int i = 0; i < n; i++) {if (s[i] == '@') a[++c] = i;}sort(a + 1, a + 1 + c);ll k = (c + 1) / 2;for (int i = 1; i <= c; i++) {if (i < k) ans += (a[k] - a[i] - (k - i));else ans += (a[i] - a[k] - (i - k));}cout << ans << endl;}return 0;
}


















)
