目录
- 1.激活函数由来
- 2. 常见激活函数
- 2.1 Sigmoid
- 2.2 Tanh
- 2.3 relu
1.激活函数由来
科学家对青蛙的神经元进行研究的时候发现,只有超过一定的阈值青蛙才会有反应,因此不能将多个输入做简单的加权平均,而需要一个阶梯函数也就是激活函数,激活的概念也就是
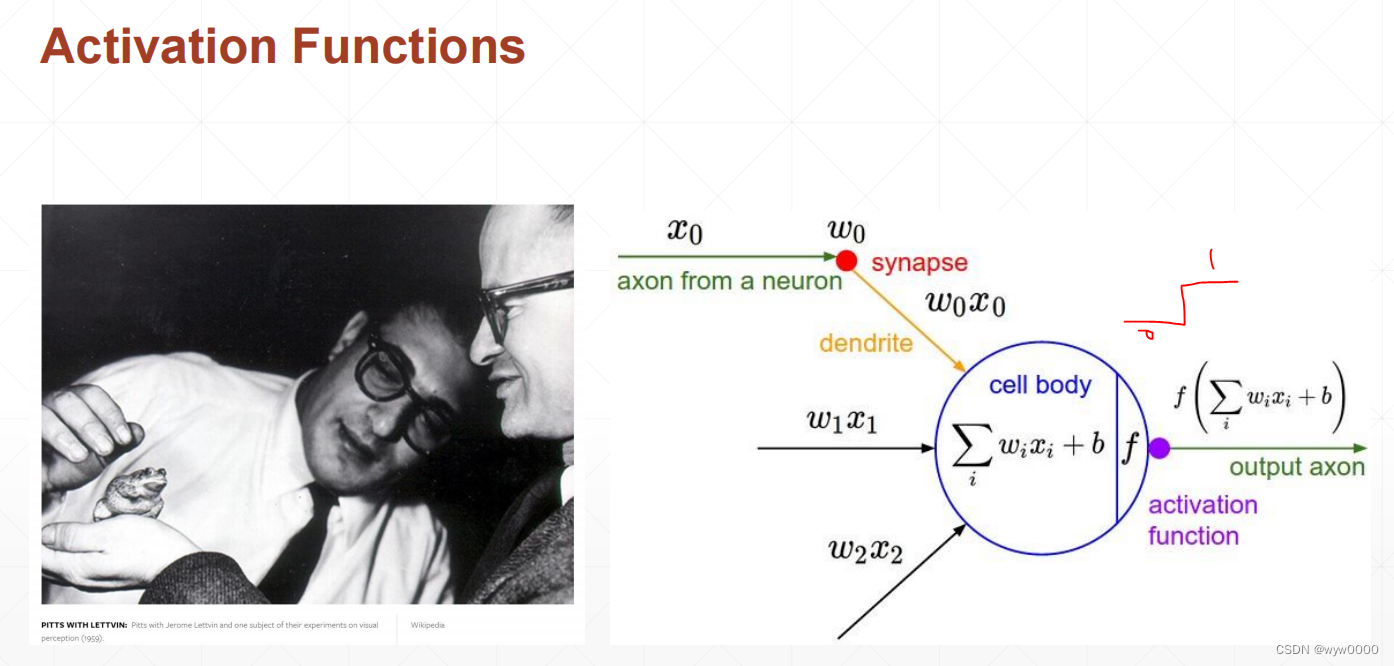
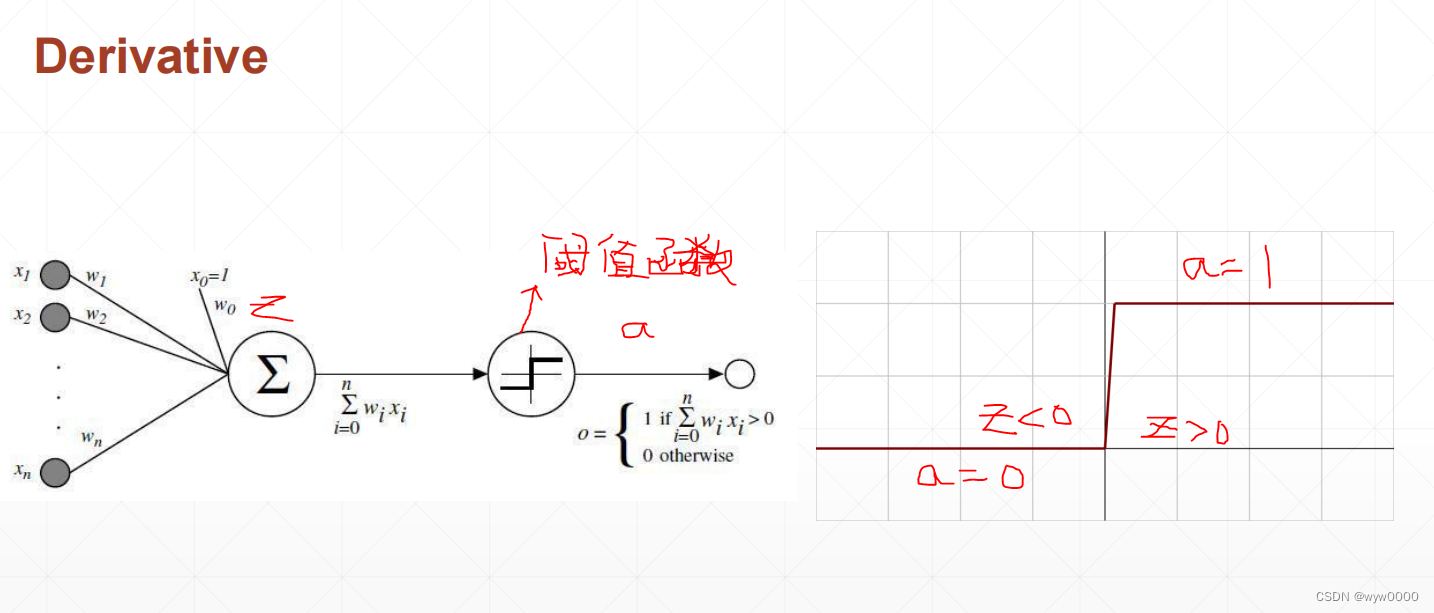
单层感知机阶梯函数不连续,因此不可导
计算机神经元模型
2. 常见激活函数
2.1 Sigmoid
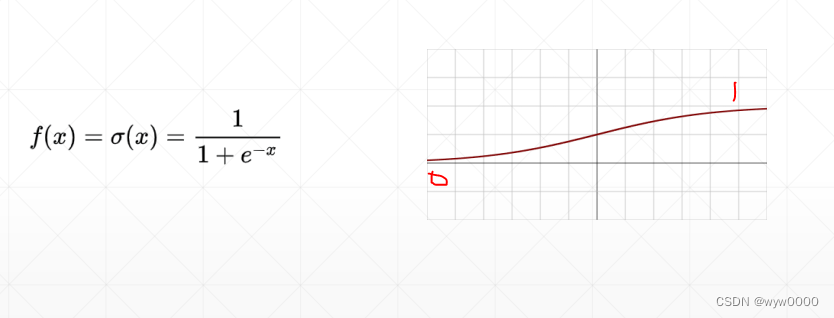
为了解决阶梯函数不可导的问题,科学家发明了sigmoid激活函数,sigmoid的值范围(0,1)
sigmoid常用于0~1的概率问题以及颜色RGB值的表示
sigmoid函数当x值趋于正无穷时,函数值接近1导数为0使得梯度一直得不到更新,从而产生梯度弥散的问题
梯度推导
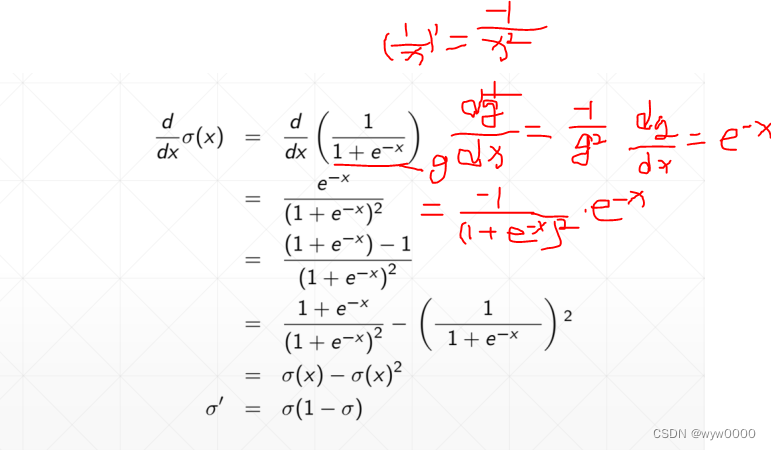

2.2 Tanh
Tanh多用于循环神经网络RNN,Tanh值的范围为[-1,1]

梯度推导
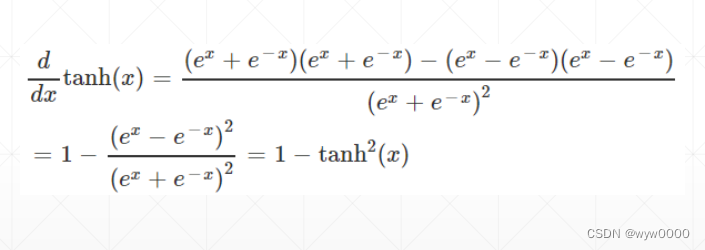

2.3 relu
relu函数是目前用的最多的激活函数,当x<0时导数为0,x>0时导数为1,函数值x<0时为0,x>0时线性变换。
relu梯度在x>0时是1,使得梯度计算时,梯度不会放大也不会缩小,因此不容易出现梯度弥散和梯度爆炸的情况




)

![[vscode]将命令行参数传递给调试目标](http://pic.xiahunao.cn/[vscode]将命令行参数传递给调试目标)
)



)


组合结构的贝叶斯优化)
)


)
-67二进制求和)

