给定一棵二叉树的后序遍历和中序遍历，请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式：
输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式：
在一行中输出该树的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。
输入样例：
7
2 3 1 5 7 6 4
1 2 3 4 5 6 7输出样例：
4 1 6 3 5 7 2解题思路
解决这个问题，我们首先需要理解二叉树的后序遍历、中序遍历以及层序遍历的基本概念：
- 后序遍历：首先访问左子树，然后访问右子树，最后访问根节点。
- 中序遍历：首先访问左子树，然后访问根节点，最后访问右子树。
- 层序遍历：按照树的层次从上到下、从左到右进行访问。
要根据给定的后序遍历和中序遍历结果重建二叉树，然后进行层序遍历。这个过程可以分为两个步骤：
步骤一：重建二叉树
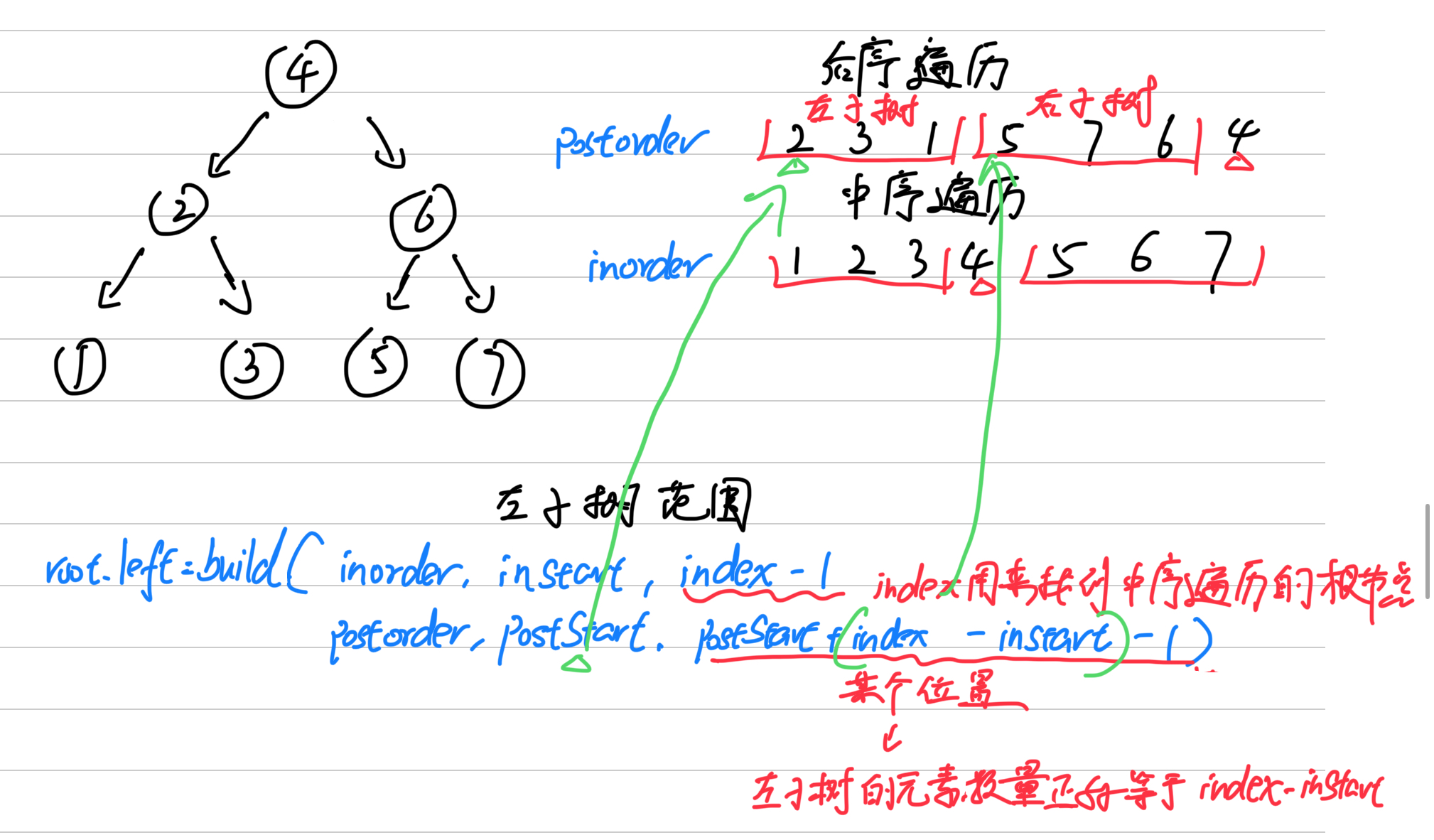
- 后序遍历的最后一个元素为树的根节点。利用这一点，我们可以在中序遍历的序列中找到根节点的位置，从而确定左右子树的中序遍历序列。
- 在中序遍历序列中，根节点左边的为左子树，右边的为右子树。根据左、右子树的节点数量，我们可以在后序遍历的序列中分别找到左右子树的后序遍历序列。
【补充：
当我们找到根节点在中序遍历数组中的位置index后：
- 左子树的中序遍历结果是inorder数组中从inStart到index-1的部分。
- 右子树的中序遍历结果是inorder数组中从index+1到inEnd的部分。
对于后序遍历数组：
- 左子树的后序遍历结果是postorder数组中从postStart到某个位置的部分。这个“某个位置”需要根据中序遍历结果来确定，具体是postStart + index - inStart - 1。这是因为左子树的元素数量正好等于index - inStart，即中序遍历中根节点左侧元素的数量。
- 右子树的后序遍历结果是postorder数组中从postStart + index - inStart到postEnd-1的部分。
】
- 重复上述过程，对左右子树分别递归执行，直到所有的节点都被处理。
步骤二：层序遍历重建后的二叉树
- 使用队列进行层序遍历。首先将根节点加入队列，然后：
-
- 从队列中取出一个节点。
- 访问该节点。
- 如果左子节点存在，将左子节点加入队列。
- 如果右子节点存在，将右子节点加入队列。
- 重复步骤1-4，直到队列为空。
解题代码
import java.io.BufferedReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;public class Main {static class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val = x; }}// 重建二叉树public static TreeNode buildTree(int[] inorder, int[] postorder) {if (inorder == null || postorder == null || inorder.length != postorder.length) {return null;}return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);}private static TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {if (postStart > postEnd) {return null;}TreeNode root = new TreeNode(postorder[postEnd]);int index = inStart;while (index <= inEnd && inorder[index] != postorder[postEnd]) {index++;}root.left = build(inorder, inStart, index - 1, postorder, postStart, postStart + index - inStart - 1);root.right = build(inorder, index + 1, inEnd, postorder, postStart + index - inStart, postEnd - 1);return root;}// 层序遍历public static void levelOrder(TreeNode root) {if (root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);boolean isFirst = true; // 添加标志变量while (!queue.isEmpty()) {TreeNode node = queue.poll();if (isFirst) {System.out.print(node.val);isFirst = false;} else {System.out.print(" " + node.val); // 在每个数字前添加空格}if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);// 假设这些值是通过输入获取的int N = scanner.nextInt();int[] postorder = new int[N];int[] inorder = new int[N];for (int i = 0; i < N; i++) {postorder[i] = scanner.nextInt();}for (int i = 0; i < N; i++) {inorder[i] = scanner.nextInt();}TreeNode root = buildTree(inorder, postorder);levelOrder(root);}
}
