数据结构与算法第二套试卷大题

1.选择排序，插入排序的思路

1.1选择排序思路：
1.每次在数组中选一个最小的元素与第一个元素进行交换——>2.然后逐步缩小数组，重复第一，二步
1.2举例：
假设有一个无序数组 [5, 2, 8, 3, 1]，使用选择排序的思路，首先找到最小的元素 1，与数组的第一个元素 5 交换位置，得到 [1, 2, 8, 3, 5]，然后在剩余的部分中找到最小的元素 2，与第二个元素 2 交换位置，得到 [1, 2, 8, 3, 5]，以此类推，最终得到有序数组 [1, 2, 3, 5, 8]；
时间复杂度：0(n^2)，空间复杂度：0(1)

2.1插入排序思路：
1.从第二个元素开始，与前面的元素对比，排序到合适的位置——>2.然后重复遍历后面的元素，重复1，2操作
2.2举例：
假设有一个无序数组 [7, 3, 5, 1, 9]，使用插入排序的思路，首先将第二个元素 3 插入到已排序部分 [7] 的正确位置，得到 [3, 7, 5, 1, 9]，然后将第三个元素 5 插入到已排序部分 [3, 7] 的正确位置，得到 [3, 5, 7, 1, 9]，以此类推，最终得到有序数组 [1, 3, 5, 7, 9]
插入排序最优：0(n)，平均为0(n^2)，空间与上述类似

2.链表操作：

设指针变量p指向双向链表中结点A，指针变量q指向被插入结点B，要求给出在结点A的后面插入结点B的操作序列（设双向链表
中结点的两个指针域分别为llink和rlink）。
答案：

q->left=p;
q-right=p->right;
p->right->left=q;
p->right=q;

3.孩子兄弟表示法画二叉树

设一棵树T中边的集合为{(A，B)，(A，C)，(A，D)，(B，E)，(C，F)，(C，G)}，要求用孩子兄弟表示法（二叉链表）表示出该树的存储结构并将该树转化成对应的二叉树
方法：抓住左孩子右兄弟即可
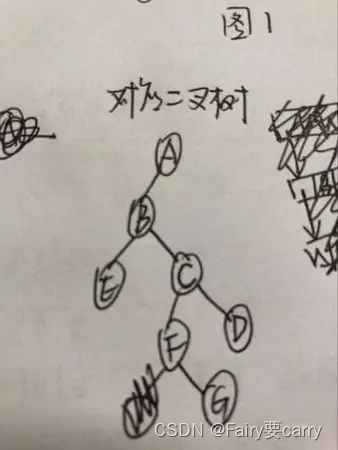
在这里插入图片描述

4.二叉排序树

核心： 左边小，根节点第二，右子树最大即可

5.prim算法构造最小生成树

根贪心类似，1.从第一个顶点搜索权值最小的第二节点，绘制路线后，2.从第二各节点再往后搜**（需要判断之前的节点是否有较小的相邻路径**，如果有，就走之前节点的，其次是需要判断是否构成环 ）
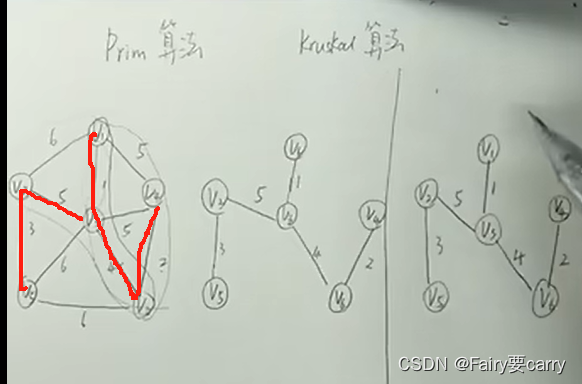
请添加图片描述
而克鲁斯卡尔算法的话，他是先把边全部排序好，按权值从小到大进行绘制，如果构成环就跳过

6.集合的表示问题

设有两个集合A和集合B，要求设计生成集合C=A∩B的算法，其中集合A、B和C用链式存储结构表示。

//1.节点结构
typedef struct Node{int data;struct Node* next;
}Node; //后续表示节点直接Node* node即可//2.链表结构
typedef struct LinkedList{Node* head; //节点
}LinkedList; //LinkedList* list表示链表//3.初始化链表
void initLinkedList(LinkedList* list){list->head=NULL;
}//4.向链表中插入元素
void insert(LinkedList* list,int data){//1.创建节点newNode并赋值Node*new_node=(Node*)malloc(sizeof(Node));new_node->data=data;new_node->next=NULL;//2.插入if(list->head==NULL){list->head=new_Node;}else{//2.2得到头节点Node* current=list->head;//2.3遍历到尾部while(current->next){current=current->next;}//2.3将新的节点插入链表尾部current->next=new_Node;}}// 生成集合C = A ∩ B
LinkedList inersect(LinkedList* list_a,LinkedList* list_b){LinkedList* result;//1.初始化链表initLinkedList(result);//2.遍历Node* current_a=list_a->head; //先得到链表a的头节点while(current_a!=NULL){Node* current_b=list_b->head; //链表b的头节点while(current_b!=NULL){if(current_a->data==current_b->data){//满足条件：两链表出现节点相同时，插入cinsert(result,current_a->data);break;  }//没有找到与a链表相同的节点，继续遍历current_b=curent_b->next;}//遍历a链表current_a=current_a->next;}return result;
}