【MATLAB第98期】基于MATLAB的MonteCarlo蒙特卡罗结合kriging克里金代理模型的全局敏感性分析模型【更新中】

【MATLAB第98期】基于MATLAB的Monte Carlo蒙特卡罗结合kriging克里金代理模型的全局敏感性分析模型【更新中】

PS:因内容涉及较多，所以一时半会更新不完
后期会将相关原理，以及多种功能详细介绍。
麻烦点赞收藏，及时获取更新消息。

引言

在前面几期，介绍了局部敏感性分析法和sobol全局敏感性分析模型，本期介绍基于kriging克里金模型的GSA全局敏感性分析方法。

往期文章：

【MATLAB第31期】基于MATLAB的降维/全局敏感性分析/特征排序/数据处理回归问题MATLAB代码实现(持续更新)
【MATLAB第32期】【更新中】基于MATLAB的降维/全局敏感性分析/特征排序/数据处理分类问题MATLAB代码实现
【MATLAB第63期】基于MATLAB的改进敏感性分析方法IPCC，拥挤距离与皮尔逊系数法结合实现回归与分类预测
【MATLAB第64期】【保姆级教程】基于MATLAB的SOBOL全局敏感性分析模型运用（含无目标函数，考虑代理模型）

一、Kriging克里金模型

克里金模型讲解参考博主：
steelDK
傻傻虎虎

克里金（Kriging）模型是一种基于空间相关性的插值方法，通过建立半变异函数来描述空间相关性，并利用已知观测点的数值和空间位置来预测未知点的数值。常用于地质、地理和环境科学等领域。
克里金模型的基本原理是通过建立半变异函数来描述空间相关性。半变异函数可以测量两个点之间的相似性程度，它表示两个点之间的数值差异随距离增加而变化的速率。常见的半变异函数包括指数模型、高斯模型和球模型等。克里金模型在应用时有如下假设条件：
(1)、克里金法假设所有数据之间都服从n维的正态分布。
(2)、无偏。
————————————————

克里金模型优点：
1.精度高
Kriging模型通过对已有数据的空间相关性进行建模，能够较准确地估计未观测点的数值，尤其适用于连续变量的插值。
2.不受外部影响
Kriging模型不仅仅依赖于周围点的数值，还考虑了点之间的空间相关性。因此，它对异常值和局部波动有较好的免疫性，能够提供相对稳定的估计结果。
3.提供不确定性估计
Kriging模型不仅能够给出点估计值，还能给出估计的不确定性。通过计算协方差函数，可以得到预测值的方差和置信区间，提供了对预测结果的可靠性评估。

克里金模型缺点：
1.数据需满足空间相关性
Kriging模型的建立基于变量的空间相关性，因此，如果数据的空间相关性很弱或不存在，模型可能不适用。此外，Kriging模型对于大数据量的计算需求较高。
2.对模型参数的选择敏感
Kriging模型的结果受到模型参数的影响，包括半方差函数的参数和拟合方法等。选择合适的参数值对于结果的准确性很重要，但也较为困难。
3.不适用于非线性插值
Kriging模型是一种线性插值方法，对于非线性、非正态的数据拟合效果较差。在这种情况下，可能需要使用其他插值方法。
4.计算复杂度较高
Kriging模型在进行预测时需要计算协方差矩阵的逆矩阵，这一过程的计算复杂度较高，尤其是当数据量较大时会增加计算的困难度。

二、蒙特卡洛模拟

（1）评价指标

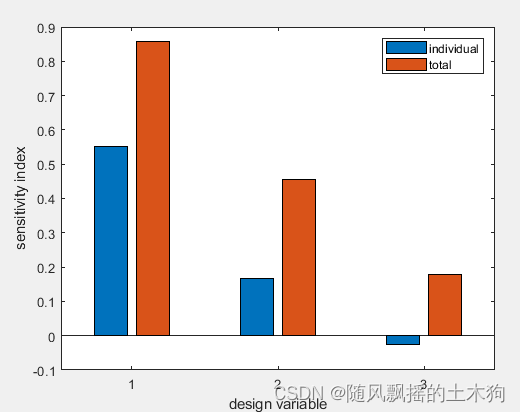
评价指标包括：一阶影响指数S，总效应指数ST**

*一阶影响指数S：*显示由各个输入变量的方差产生的因变量的方差，根据一阶影响指数可以量化单个变量对模型的敏感程度

总效应指数ST：显示由每个输入变量的方差及其与其他输入变量的相互作用而产生的因变量的方差。

（2）参数

使用MCGSA函数蒙特卡罗进行全局灵敏度分析，即使用蒙特卡罗模拟计算个体效应和总效应（仿照Sobol方差计算）。其中，四个参数包括（func、str、bounds、npop）：
输入参数：

func是代理结构
str是字符串标识代理项
bounds是定义用于拟合代理项的输入空间的矩阵（第一行和第二行分别是下限和上限）
npop是蒙特卡罗样本的数量（npop一般大于5000）

输出参数：

output是指分析结果（结构变量）：

其中，individual ：个体效应矩阵结构（一阶影响指数S）
total：总效应矩阵结构（总效应指数ST）。

三、全局敏感性分析（有目标函数）

VarMin=[0 0 0];%各个参数下限
VarMax=[10  10 10];%各个参数上限
bounds=[VarMin;VarMax]% 创建DoEdim       = 3;% 优化变量数量numpop = 20;%采样点个数,也就是参数水平数 ,取大了好，比如4000，但慢X = lhsdesign(numpop, dim);% 拉丁超立方抽样%X= sobolset(dim);%或者参考64期sobol抽样方法。 % 目标函数响应
for i=1:numpopY(i,:) = myfun(X(i,:)); %
end

A、设定目标函数（3个变量，即维度D=3）
Y=X1^2+2*X2+X3-1

y=x(1)^2+2*x(2)+x(3)-1;

B、设定变量上下限

VarMin=[0 0 0];%各个参数下限
VarMax=[10  10 10];%各个参数上限

C、建立克里金模型

训练集输入输出建立：

X = lhsdesign(numpop, dim);% 拉丁超立方抽样%X= sobolset(dim);%或者参考64期sobol抽样方法。 % 目标函数响应
for i=1:numpopY(i,:) = myfun(X(i,:)); %
end

模型拟合：

opt  = krigingtrain(X, Y);kopt = krigingfit(opt );

D、设定MC参数

npop = 200; %蒙特卡罗模拟的点数

% 创建A矩阵
Xa = rand(npop, dim);
Xa = SV(Xa, [zeros(1,dim); ones(1,dim)], Xa);% 创建B矩阵
Xb = rand(npop, dim);
Xb = SV(Xb, [zeros(1,dim); ones(1,dim)], Xa);

E、GSA分析