一、特征工程

1. 为什么需要对数值类型的特征做归一化？

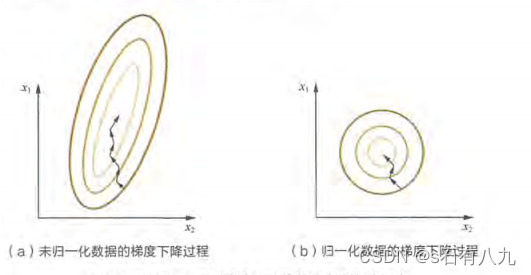
（1）对数值类型的特征做归一化可以将所有的特征都统一到个大致相同的数值区间内；
（2）可以加快梯度下降收敛的速度，归一化后让等高线的分布更加均匀在一个范围内，类似于一个圆，减少求解过程中参数寻优的震荡，更加快找到最优解。

2. 文本表示模型

• 词袋模型（ Bag of Words，把每篇文章看成一袋子词，忽略顺序，用频率估量单词重要性) ；
• TF-IDF (Term Frequency-Inverse Document Frequency ）；
• 主题模型（ Topic Model ，从文本库中发现有代表性的主题，计算主题分布）；
• 词嵌入模型（ Word Embedding ，是将每个词都映射成低维空间上的K维向量) Word2Vec 是目前最常用的词嵌入模型之 一。Word2Vec 实际是一种浅层的神经网络模型， 有两种网络结构，分别是 CBOW (Continues Bag of Words ）和 Skip-gram。

3. 图像数据不足的处理方法

（1）一定程度内的随机旋转、平移、缩版、裁剪、填充、左右翻转等，这些变换对应着同个目标在不同角度的观察结果。
（2）对图像中的像素添加躁声扰动，比如椒盐噪声、高斯白噪声等。
（3）颜色变换。
（4）改变图像的亮度、清晰度、对比度、锐度等。

二、模型评估

1.常见的评估指标

准确率（ Accuracy ），精确率（ Precision ），召回率（ Recall ），均方根误差(Root Mean Square Error, RMSE)。F1 score ROC 曲线也能综合地反映一个排序模型的性能。
F1 score 是精准率和召回率的调和平均值

RMSE 能够很好地反映回归模型预测值与真实值的偏离程度。但在实际问题中，如果存在个别偏离程度非常大的离群点( Outlier ）时，即使离群点数 非常少，也会让 RMSE 指标变得很差。可以使用平均绝对百分比误差（ Mean Absolute Percent Error, MAPE）相比 RMSE, MAPE 相当于把每个点的误差进行了归一化，降低了个别离群点带来的绝对误差的影响。

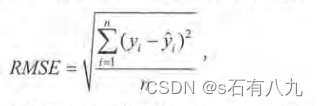
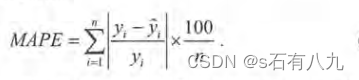
2.ROC曲线

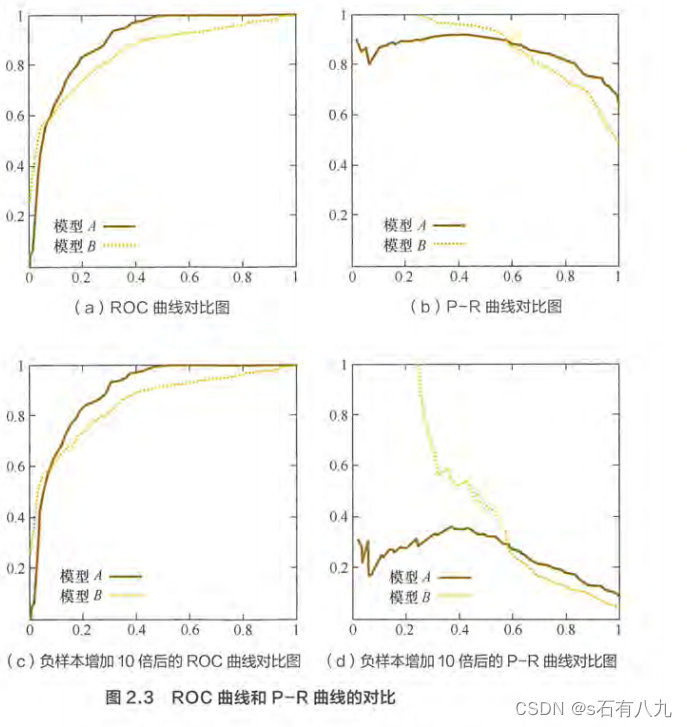
ROC 曲线，曲线下的面积（ Aera Under Curve, AUC) ；P-R曲线

• ROC 曲线的横坐标为假阳性率（ False Positive Rate, FPR ），纵坐标为真阳性率（ True Positive Rate, TPR）①真阳性（True Positive，TP）：样本的正例被预测为正例，预测正确；②假阳性（False Positive，FP）：样本的负例被预测成正例，预测错误。AUC指的是 ROC 曲线下的面积大小，AUC越大，说明分类器越可能把真正的正样本排在前面 分类性能越好。
• 在样本不均衡时，选择ROC曲线能更好的反映模型本身好坏，适用场景多。（当 负样本的分布发生变化时， ROC 曲线的形状能够基本保持不变，而P-R曲线的形状一般会发生较剧烈的变化）
  

3.为什么在一些场景中要使用余弦相似度而不是欧氏距离？

（1）欧氏距离体现数值上的绝对差异，而余弦相似度体现方向上的相对差异。
（2）欧式距离的数值受维度的影响，范围不固定。余弦相似度更关注相对差异，即向量之间的角度关系。不论是在高维还是低维空间，依然保持“相同时为1，正交时为0，相反时为-1”的性质。
（3）例如，用户A（1,0）和用户B（0,1），采用欧氏距离会很小，采用余弦相似度会很大。如果想要表示用户之间的相对差异时，余弦相似度会更好。
再比如，用户A（1,10）和用户（1,100），采用欧氏距离会很大，采用余弦距离会很近。如果更关注数值绝对差异，使用欧氏距离会更好。

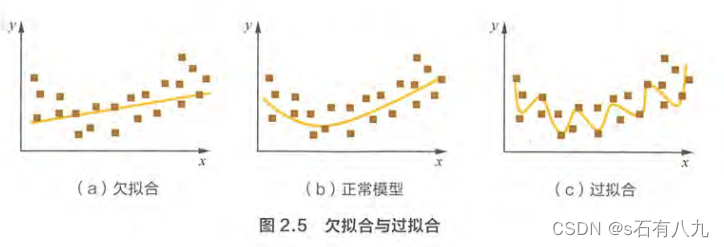
4.过拟合和欠拟合

过拟合：对训练数据拟合太过贴合，训练集上很好，测试集很差；
欠拟合：训练和预测都不好，没学到位。

• 降低“过拟合”：
  （1）数据上，更多数据（扩充、数据增强、生成式对抗网络合成数据）；
  （2）降低模型复杂度；
  （3）正则化，避免权值过大带来过拟合；
  （4）集成学习，集成多个模型。
• 降低“欠拟合”：
  （1）添加新特征；
  （2）增加模型复杂度；
  （3）减小正则化系数。

三、经典算法

1.支持向量机SVM

SVM 模型推导，核函数，SMO (Sequential Minimal Optimization ）算法
支持向量机（support vector machines, SVM）是一种二分类模型，①它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；②SVM还包括核技巧，这使它成为实质上的非线性分类器。
（SVM 实际上是在为找到木棒的最佳放置位置，使得两边的球都离分隔它们的木棒足够远。）

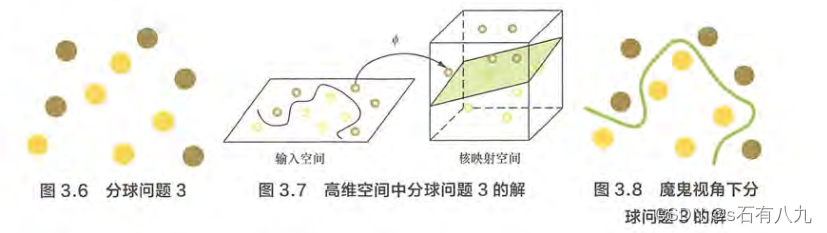
• 对于任意线性可分的两组点， 它们在 SVM 分类的超平面上的投影都是线性不可分的。
• 核函数的引入一方面减少了我们计算量，另一方面也减少了我们存储数据的内存使用量。常用核函数有：线性核函数、多项式核函数、高斯核函数。

优点：

• 数学理论支持，可解释性强；
• 采用核技巧之后，可以处理非线性分类/回归任务。

缺点：

• 训练时间长。
• 模型预测时，预测时间与支持向量的个数成正比。当支持向量的数量较大时，预测计算复杂度较高。

因此支持向量机目前只适合小批量样本的任务，无法适应百万甚至上亿样本的任务。

2.逻辑回归

逻辑回归，线性回归，多标签分类， Softmax

1. 逻辑回归处理的是分类问题，分类问题是指因变量是离散的，比如二分类（0或1），多分类（A，B，C等）。
   线性回归处理的是回归问题，回归问题是指因变量是连续的，比如房价，身高等。这是两者的最本质的区别。
2. 线性回归使用最小二乘法（使所有点到直线的距离之和最小，就是使均方误差最小化）作为参数估计方法，逻辑回归使用极大似然法（极大似然函数反映了参数与数据的匹配程度，越大说明越匹配，越有可能是真实的参数值）作为参数估计方法。

线性回归的模型如下：

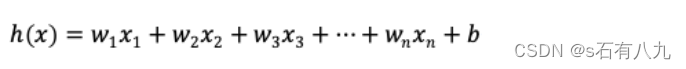
线性回归得出的模型不一定是一条直线，在只有一个变量的时候，模型是平面中的一条直线；有两个变量的时候，模型是空间中的一个平面；有更多变量时，模型将是更高维的。

3. 非线性回归: 非线性回归模型的形式可以是任意的非线性函数，例如多项式函数 (至少有一个变量的指数不是1)、指数函数、对数函数等。它的形态是曲线形态。非线性回归模型假设因变量与自变量之间的关系是非线性的。

问题：当使用逻辑回归处理多标签的分类问题时，有哪些常见做法，分别应用于哪些场景，他们之问又有怎样的关系？
当存在样本可能居于多个标签的情况时，我们可以训练k个二分类的逻辑回归分类器。第i个分类器用以区分每个样本是否可以归为第i类，训练该分类器时，需要把标签重新整理为“第i类标签”与“非第i类标签”两类。

3.决策树

决策树的决策过程，例子如下：

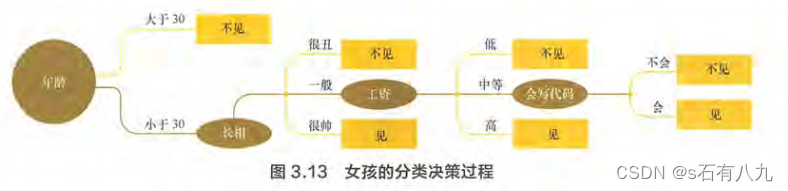
将决策树应用集成学习的思想 以得到随机森林、梯度提升决策树等模型。
决策树的生成包含了特征选择、树的构造、树的剪枝三个过程。

问题1：决策树有哪些常用的启发函数？

1. ID3一一最大信息增益
   只能处理离散型变量；
   用于分类任务；
   对样本特征缺失值比较敏感；
   通过剪枝来权衡树的准确性与泛化能力。
2. C4.5一一最大信息增益比
   处理连续型变量，将连续型变量转换为多个取值区间的离散型变量；
   用于分类任务；
   通过剪枝来权衡树的准确性与泛化能力。
3. CART一一最大基尼指数（ Gini )
   构建是每次都会对特征进行二值划分，很好适用于连续型变量；
   分类、回归都可以；
   用全部数据发现所有可能的树结构进行对比。

问题2：如何对决策树进行剪枝？
决策树很可能会过拟合，需要剪枝来提升模型泛化能力。
剪枝两种方法：预剪枝和后剪枝。

• 预剪枝： 在生成决策树的过程中提前停止树的增长。
  结点拓展之前，若计算不能带来模型能力提升，不再生长子树。
  简单高效，适合解决大规模问题。不易估计何时停止树的生长，有欠拟合风险。

• 后剪枝： 先生成完全的决策树，再从底层向上计算是否剪枝。
  剪枝过程将子树删除，用一个叶子结点替代。
  可以得到泛化能力更强的决策树，但时间开销会更大。

四、降维

1.主成分分析（ Prinal Components Analysis, PCA ）降维中最经典的方法

问题1：如何定义主成分？从这种定义出发，如何设计目标函数使得降维达到提取主成份的目的？针对这个目标函数，如何对 PCA 问题进行求解？
PCA 旨在找到数据中的主成分，并利用这些主成分表征原始数据从而达到降维的目的。PCA 的求解方法如下：

问题2：PCA 求解的真实是最佳投影方向，即一条直线，这与数学中线性回归问题的目标不谋而合，能否从回归的角度定义 PCA 的目标并相应地求解问题呢？
从最小化回归误差来定义和求解 PCA 的问题。这时，我们可以把 PCA 看作是一种无监督的回归方法，它没有区分输入变量和输出变量，而是将所有的变量都视为同等重要的。我们的目标是找到一个 d 维超平面，使得数据点到这个超平面的距离平方和最小。这相当于用一个低维的线性模型来拟合数据的分布，从而达到降维的目的。

2.线性判别分析LDA（有监督，对数据降维）

问题：LDA、PCA 作为经典的降维算法，他们的不同是？

1. 目标不同： ①PCA 选择的是投影后数据方差最大的方向，也就是保留了数据的最大信息量。PCA 是无监督的，它不考虑数据的类别标签，只是用主成分来表示原始数据，去除冗余的维度，达到降维的目的。②LDA 选择的是投影后类内方差小、类间方差大的方向，也就是使得数据的判别性最强。LDA 是有监督的，它利用了数据的类别标签信息，为了找到数据中具有判别性的维度，使得原始数据在这些方向上投影后，不同类别尽可能区分开。
2. 结果不同： ①PCA 降维后的数据可能会混合不同类别的数据，导致分类效果不佳。②LDA 降维后的数据能够较好地保留类别信息，提高分类效果。
3. 应用不同： ①PCA 主要在无监督的任务中使用，例如数据压缩、降噪、可视化等。②LDA 主要在有监督的任务中使用，例如分类、特征选择等。一般来说，对于无监督的任务，可以使用 PCA 先进行降维，过滤掉一些噪声和冗余的特征。对于有监督的任务，可以使用 LDA 对数据进行降维，提取出具有判别性的特征。

一个基本的原则一一对无监督的任务使用 PCA 进行降维，对有监督的则应用 LDA。