八数码难题
题目描述
在 3 × 3 3\times 3 3×3 的棋盘上,摆有八个棋子,每个棋子上标有 1 1 1 至 8 8 8 的某一数字。棋盘中留有一个空格,空格用 0 0 0 来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局(初始状态)和目标布局(为了使题目简单,设目标状态为 123804765 123804765 123804765),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
输入格式
输入初始状态,一行九个数字,空格用 0 0 0 表示。
输出格式
只有一行,该行只有一个数字,表示从初始状态到目标状态需要的最少移动次数。保证测试数据中无特殊无法到达目标状态数据。
样例 #1
样例输入 #1
283104765
样例输出 #1
4
提示
样例解释
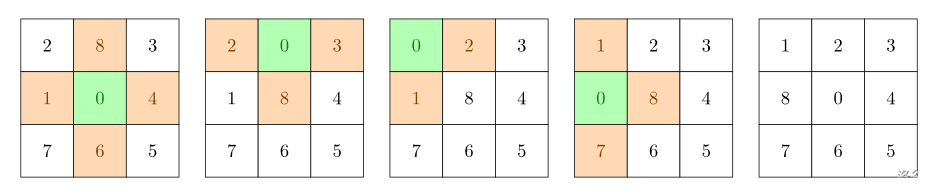
图中标有 0 0 0 的是空格。绿色格子是空格所在位置,橙色格子是下一步可以移动到空格的位置。如图所示,用四步可以达到目标状态。
并且可以证明,不存在更优的策略。
广度优先搜索
算法思想
根据题目描述,输入一个棋盘的初始状态,求从初始状态到目标状态需要的最少移动次数,可以用广度优先搜索求解,基本思想如下:
- 将初始状态 start \text{start} start的移动步数设为 0 0 0,然后将其加入队列
- 只要队列不为空
- 从队首取出一个状态 state \text{state} state
- 如果 state = end \text{state}=\text{end} state=end结束状态,则搜索结束,返回到达的 state \text{state} state移动步数
- 否则,找到 state \text{state} state中字符 0 0 0的位置,向相邻方向进行扩展
- 如果扩展到一个新的状态,则计算扩展到新状态的步数,并将新状态加入队列
代码实现
#include <bits/stdc++.h>
using namespace std;
queue<string> q;
unordered_map<string,int> dis;int dx[]={-1, 1, 0, 0}, dy[]={0, 0, -1, 1};int bfs(string start)
{string end = "123804765";dis[start] = 0;q.push(start);while(!q.empty()){string state = q.front(); q.pop();int step = dis[state];if(state == end) return step;int k = state.find('0'); //在当前状态的字符串中找到字符0int x = k / 3, y = k % 3; //将字符串中的位置转换为矩阵中的坐标for(int i = 0; i < 4; i ++){int a = x + dx[i], b = y + dy[i]; if(a < 0 || a >= 3 || b < 0 || b >= 3) continue; //越界swap(state[k], state[a * 3 + b]); //将数字字符与0进行交换,转移到新状态if(!dis.count(state)) //没有访问过{ dis[state] = step + 1; //转移到state状态的最小步数q.push(state); //入队}swap(state[k], state[a * 3 + b]); //恢复现场,交换回来,为下次转移做准备}}return -1;
}int main()
{string start;char c;for(int i = 0; i < 9; i ++){cin >> c;start += c;}cout << bfs(start) << endl;return 0;
}
A*算法
通过BFS可以发现,对每个状态都可以将 0 0 0向上右下左四个方向进行扩展,在最坏情况下要搜索的状态空间为 4 9 4^9 49,指数级别,搜索的效率比较低。在这种情况下,可以使用A*算法进行求解。
A*(A Star)算法是一种很常用的路径查找和图形遍历算法,它有较好的性能和准确度。
A*算法通过下面的函数来计算每个状态的优先级:
f ( n ) = g ( n ) + h ( n ) f(n)=g(n) + h(n) f(n)=g(n)+h(n)
其中:
- f ( n ) f(n) f(n)是当前状态 n n n的综合优先级。当选择下一个要扩展的状态时,我们总会选取综合优先级最高(值最小)的状态。
- g ( n ) g(n) g(n)是状态距离起点(初始状态)的代价
- h ( n ) h(n) h(n)是状态 n n n距离终点(目标状态)的预计代价,这也就是A*算法的启发函数。
算法思想
A*算法与BFS类似,不同之处在于A*算法使用优先队列,选取 f ( n ) f(n) f(n)值最小(优先级最高)的状态作为下一个待扩展的状态。基本思想如下:
- 将初始状态 start \text{start} start的移动步数设为 0 0 0,然后其综合优先级和初始状态加入优先队列
- 只要队列不为空
- 取出优先队列中综合优先级最高(值最小)的状态 state \text{state} state
- 如果 state = end \text{state}=\text{end} state=end结束状态,则搜索结束,返回到达的 state \text{state} state移动步数
- 否则,找到 state \text{state} state中字符 0 0 0的位置,向相邻方向进行扩展
- 如果扩展到一个新状态,或者到达该状态的步数减少,将状态的综合优先级和状态本身继续加入优先队列
启发函数
从算法的基本思想可以看出来,启发函数会影响A*算法的行为。
- 在极端情况下,当启发函数 h ( n ) h(n) h(n)为0时,则将由 g ( n ) g(n) g(n)决定状态的优先级,此时算法就退化成了Dijkstra算法。
- 如果 h ( n ) h(n) h(n)始终小于等于状态 n n n到终点的代价,则A*算法保证一定能够找到最短路径。但是当 h ( n ) h(n) h(n)的值越小,算法将遍历越多的状态,也就导致算法越慢。
- 如果 h ( n ) h(n) h(n)完全等于状态 n n n到终点的代价,则A*算法将找到最佳路径,并且速度很快。可惜的是,并非所有场景下都能做到这一点。因为在没有达到终点之前,很难确切算出距离终点还有多远。
- 如果 h ( n ) h(n) h(n)的值比状态 n n n到终点的代价要大,则A*算法不能保证找到最短路径,不过此时会很快。
通过调节启发函数我们可以控制算法的速度和精确度。因为在一些情况,可能未必需要最短路径,而是希望能够尽快找到一个路径即可,这也是A*算法比较灵活的地方。
对于网格形式的图,有以下这些启发函数可以使用:
- 如果图形中只允许朝上下左右四个方向移动,则可以使用曼哈顿距离(Manhattan distance)。
- 如果图形中允许朝八个方向移动,则可以使用对角距离。
- 如果图形中允许朝任何方向移动,则可以使用欧几里得距离(Euclidean distance)。
代码实现
#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>
using namespace std;
typedef pair<int, string> PIS;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
//启发函数取当前状态中每个数字与其目标位置的曼哈顿距离之和
int h(string state)
{int res = 0;for(int i = 0; i < state.size(); i ++){if(state[i] != '0'){int t = state[i] - '1';res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3); //累加每个数字到其正确位置的曼哈顿距离}}return res;
}
int bfs(string start)
{string end = "123804765";priority_queue<PIS, vector<PIS>, greater<PIS>> heap; //小顶堆unordered_map<string, int> dis; //记录到达每一种状态的步数//g(start)返回起点到终点的预估距离heap.push({0 + h(start), start});dis[start] = 0;while(heap.size()){PIS t = heap.top(); heap.pop();string state = t.second;if(state == end) break; //终点第一次出队,搜索结束int step = dis[state];int k = state.find('0'); //找到0所在位置int x = k / 3, y = k % 3; for(int i = 0; i < 4; i ++){int a = x + dx[i], b = y + dy[i];if(a < 0 || a >= 3 || b < 0 || b >= 3) continue;swap(state[x * 3 + y], state[a * 3 + b]); //将0和目标交换if(!dis.count(state) || dis[state] > step + 1) //如果扩展到一个新的状态,或者能够缩短到state的距离{dis[state] = step + 1;heap.push({dis[state] + h(state), state}); //将综合优先级和状态加入优先队列}swap(state[x * 3 + y], state[a * 3 + b]);//恢复现场}}return dis[end];
}
int main()
{char c;string start;for(int i = 0; i < 9; i ++){cin >> c;start += c;}cout << bfs(start);return 0;
}
-- 算法导论16.1 1题)




常见算法的基本结构)






栈与队列:用栈实现队列(leetcode232))

)

(加法器))
![原生微信小程序电影购票+后台管理系统[含文档]](http://pic.xiahunao.cn/原生微信小程序电影购票+后台管理系统[含文档])

