参考资料:生物统计学
裂区设计(split-plot design)是安排多因素试验的一种方法,裂区设计对因素的安排有主次之分,适用于安排对不同因素试验精度要求不一的试验。
裂区设计时,先按第一因素的处理数划分主区,在主区里随机安排主处理,主处理在主区内可以按完全随机、随机区组或拉丁方等方式排列,然后将主区划分为副区(裂区),在裂区里随机排列第二因素的处理(副处理),副区又可以划分为小区,在小区里安排第三因素的处理,以此类推。越是低层次的小区,试验误差越小,精度越高。下面以二裂式为例进行讲解。
1、设计方法
二裂式裂区只有两个层次,划分为主区和副区,适用于两因素试验设计。由于副区的试验误差比主区小,所以将试验精度要求较高的因素作为副处理,将试验精度要求相对较低的因素安排为主处理。
2、主要特点
(1)在野外试验时,主区面积大,数量少,副区面积小,数量多。
(2)副处理的试验精度较主处理的试验精度高。
3、试验结果的统计分析
裂区设计的实验结果采用方差分析法进行统计分析。由于对副处理来说主区就是一个区组,从试验的所有处理组合来说,主区又是一个不完全区组,所以方差分析时设计区组及两因素,比骄傲复杂。方差分析时,主区和副区分开进行,变异的分解,主区分解为区组、主处理和主区误差三部分,副区分解为副处理、两因素互作和副区误差3项。数学模型为:
其中,为A因素i水平B因素j水平区组k的第l个观测值;
、
为因素的处理效应;
为因素间的互作;
为区组效应;
为主区误差,
为副区误差。平方和与自由度的分解为:
主区:
副区:
其中,下标T为总变异,下标A为主处理变异,下标B为副处理变异,下表R为区组变异,下标e(M)为主区误差,下标e(S)为副区误差;a为A因素的水平数,b为B因素的水平数,b为重复数;T_i为A因素i水平的观测值之和,T_j为B因素j水平的观测值之和,T_k为区组k的观测值之和,T_l为主区l的观测值之和,T_m为副区m的观测值之和;,T为所有观测值之和。
由于主区和副区是分别分解的,计算统计量F时,也分别用对应的误差项做分布,即:
4、案例
A因素为主区,3个水平;B因素为副区,4个水平,重复3次。试验设计即数据如下:
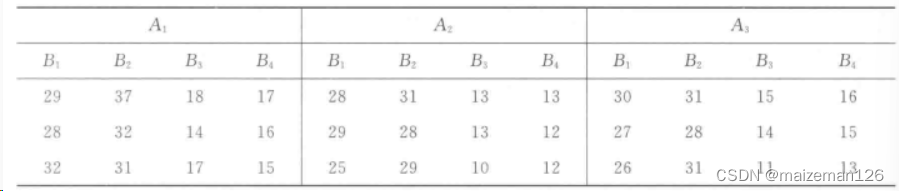
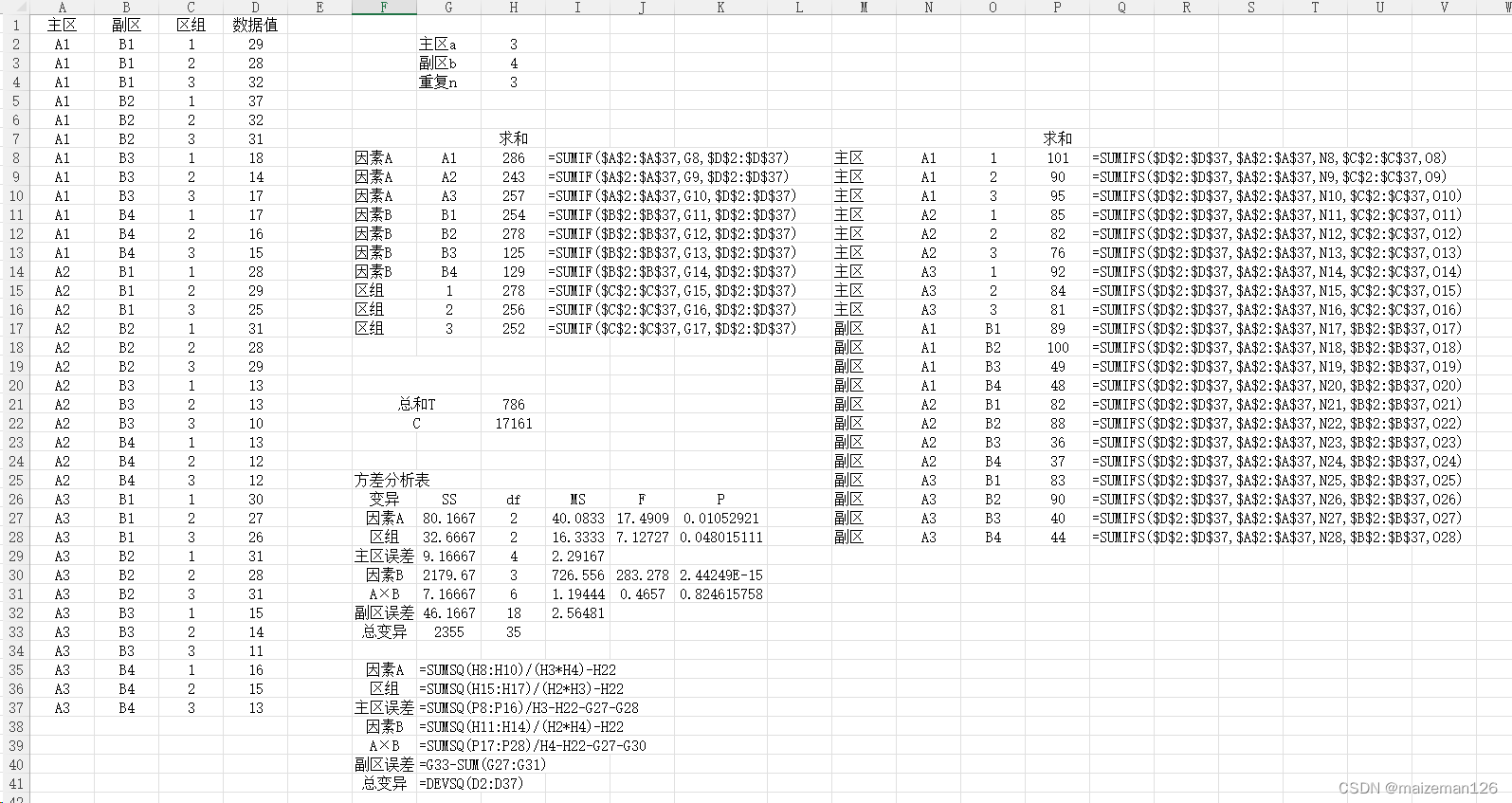
excel方差分析操作如下:



常见算法的基本结构)






栈与队列:用栈实现队列(leetcode232))

)

(加法器))
![原生微信小程序电影购票+后台管理系统[含文档]](http://pic.xiahunao.cn/原生微信小程序电影购票+后台管理系统[含文档])


)
