特征值与特征向量
已知任意向量x,现有矩阵A对x进行操作后,得到新的向量Ax。这就好比是自变量x与函数f(x)的关系一样,向量x通过类似“函数”的处理得到了一个新的向量Ax。这个新的向量可能和原向量x方向相同,也可能不同(事实上大多都不同)。此外,新的向量与原向量的长度可能向量,也可能不同。而特征向量(Eigen vector)指的就是那些和原始向量x平行的那些Ax,这是线性代数所研究的两大问题的的另一个部分(在我看来,线性代数的两个主要方向一个是研究垂直,另一个就是这里的平行)。
特征向量与特征值的意义:
对于矩阵A而言,存在一些特殊的向量x,使得矩阵A作用于向量x之后所得到的Ax任然与原向量x平行(这里的平行可理解为与x的方向相同或正好相反),得到:
满足上述描述的向量x,就被称为特征向量。其中,系数是一个数,又叫特征值(Eigen value),可以看成是向量x长度的一个倍数。可以是1,表示Ax=x即,矩阵A没有改变向量x的长度。可以是-5,即改变了x的方向和大小,可以是0.26,也可以是复数。
Tips:当特征值=0,且x不是零向量时,矩阵A应该满足什么条件呢?
答:若=0,则
x为零向量,得到Ax=0。向量x属于A的零空间(左零空间)又不是平凡解零向量,则矩阵A必须是奇异矩阵(singular matrix)才能让非零向量x通过线性组合得到零向量。这样一来,我们就得出了一条重要推导,若矩阵A为奇异矩阵,即不可逆矩阵,则矩阵A的特征值包含0。(这里我们再补充一点,对于矩阵A而言,可以有多个特征向量,对应多个特征值)。
特征向量与特征值的性质:
1,n维度矩阵A有n个特征值。
2,这n个特征值的乘积等于矩阵A的行列式。
3,n个特征值的和等于矩阵A主对角线元素的和,这个和被称为Trace(迹)。
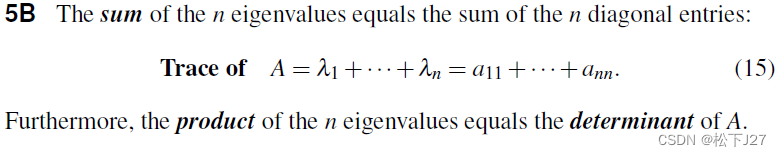
一些常见矩阵的特征向量与特征值:
1,投影矩阵P(projection matrix)
已知投影矩阵P可把任意向量投影到n维子空间S上,例如下图中,投影矩阵P作用于向量b上,得到了b在S上的投影Pb。
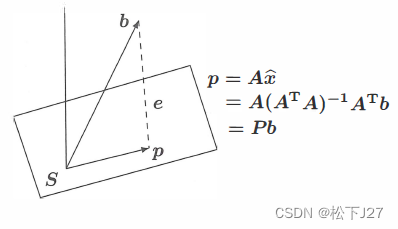
现在我们要问的是,对于投影矩阵P而言,他作用在什么向量x上,得到的结果依然与x平行?如果平行,这个新向量的长度是x的几倍呢(即,求)?根据特征向量的定义,投影矩阵P作用于x上后得到的Px应当平行于Px。那么对投影矩阵P而言,特征向量x必须是n维子空间S内的向量。因为,对子空间S内的任意向量x施加P矩阵,得到投影就是x自己。方向与x相同,且长度不变,即特征值为1。用数学表达式来表示就是:
此外,我们还知道当向量b垂直于子空间S时,b在S上的投影为零向量。因此,我们又发现了S空间之外的特征向量,即所有垂直于S空间的向量x,投影Px与x的方向相同,但长度为0。表达为数学公式就是:
小结:这里我们总结一下投影矩阵的特征向量与特征值,对于投影矩阵P而言,他的特征向量为投影矩阵P所投影的子空间内的所有向量和垂直于该子空间的所有向量。
2,置换矩阵(permutation matrix)
先看一个例子,已知置换矩阵A为(交换两个元素的位置):
同样,还是按照特征向量的定义出发,现有的置换矩阵A作用在哪个向量x上,才能使得新向量Ax平行于x?换句话说,就是要找到一个向量x,交换元素位置后仍然是x或倍的x? 明显,如果向量x中的两个元素相同,则不论怎么交换两个元素的位置,得到的结果仍是x。
例如:
因此,对于矩阵A而言,所有两个元素相同的向量x都是A的特征向量,且特征值为1。又因为,矩阵A为二维矩阵,因此,可能还存在一对特征向量与特征值。比如说,如果我们先令特征值为-1,那么就允许特征向量x中的元素大小相同但符号相反,这样一来,交换顺序再乘以-1后,得到的仍然还是x。
例如:
小结:对于置换矩阵而言,那些交换元素位置后依然还是原始向量的向量就是A的特征向量,对应的特征值为1。而那些交换元素相应位置后,只改变了符号但不改变数值的向量,也是A的特征向量,他们所对应的特征值为-1。
对于一般矩阵A,如何找到他的特征值与特征向量?
Step I: Find λ first!
首先,我们有方程:
但这里有两个未知数,因此我们把上面的方程改写一下:
这个齐次方程的解就是矩阵(A-I)的零空间,抛开平凡解全0向量不说。要想让矩阵的零空间存在非零向量,则矩阵的A必为奇异矩阵,即不可逆矩阵。同时,结合之前学到的行列式的概念,若一个矩阵是奇异矩阵,则矩阵的行列式为0。这样一来,我们就不用考虑未知数x,也就是特征向量,先求未知数
,也就是特征值。如下:
这个方程是一个非常重要的方程(Key equation),叫特征值方程(Eigen-value equation)或者叫特征方程(characteristic equation)。
Step II: Substitue λ and solve equations!
求解完特征值方程后会得到n个(可能会有相同的
),把这些
代入到经过改写后的方程组中,求解齐次方程组,或者说是求解零空间,得到相应的特征向量。
举个例子来说明上述求解过程:
对于上面提到过的置换矩阵A,第一步,我们先求det(A-λI)=0:
得到:
由此得到两个特征根:
把第一个特征值λ=1代入改写后的方程:
其中(A-I)为:
对该矩阵消元得到矩阵U,找到主元列和自由列,其中与自由列位置所对应的向量x中的元素就是自由变量。设自由变量为一个任意数,求出相应的特解。
消元矩阵U的秩为1,存在一个特解。第一列为主元列,第二列为自由列。因此,对应的自由变量为x2。令x2=1, 则x1=1得到一个特解,也就是我们要找的特征向量x:
相应的代入第二个特征值λ=-1:
令自由变量x2=1,则x1=-1:
这里我们顺便基于矩阵的行列式和迹来验证一下两个特征根:
一个特例:多个重复/相同的特征值会引发特征向量的短缺
令矩阵A为:
先求特征值:
这会得到两个重复的特征值:
带入其中一个特征值,并求特征向量:
令自由变量x1=1,得到:
现在问题来了,如果你代入第二个特征向量(还是3),并重复上述操作,你是无法找到一个与第一个特征向量线性无关的另一个特征向量了。最多你只是令自由变量x1为一个其他数,然后得到一个特征向量,但最终你得到的这个特征向量与之前得到的那个是线性相关的。
这个例子说明了一个矩阵的特征向量的线性相关性即取决于矩阵的维数也取决于是否存在重复的特征值。对于一个 2x2 的方阵,如果它有两个不同的特征值,那么就能得到两个线性无关的特征向量。但如果是两个重复的特征值,就只能得到一个特征向量或两个线性相关的特征向量。
另一个特例:特征根为复数的情况
已知旋转矩阵Q,求Q的特征向量和特征值:
(全文完)
作者 --- 松下J27
参考文献(鸣谢):
1,Introduction to Linear Algebra,Fifth Edition - Gilbert Strang
2,麻省理工Gilbert Strang教授线代大师-线性代数(全)_哔哩哔哩_bilibili
(配图与本文无关)
版权声明:文中的部分图片,文字或者其他素材,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27
)

)

工厂模式原厂Windows11预装OEM系统,含F10智能还原功能)
)




)








