611.有效三角形的个数
一、题目描述
OJ题目链接:力扣(LeetCode)
二、思路讲解
首先我们能想到的一定是暴力枚举,它的时间复杂度是(O^3)。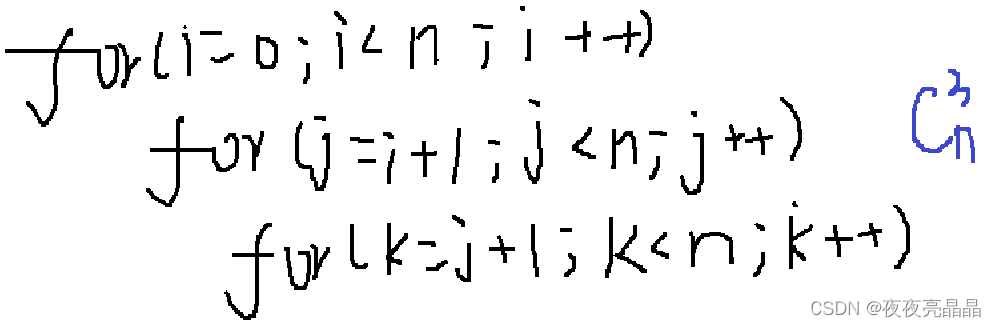
我们可以固定一个最长边,然后在比这条边小的有序数组中找出一个二元组,计算二元组和最长边的大小关系,紧接着就可以枚举出其他二元组:
1.如果该二元组 <= [最长边],则该条件对[固定二元组中较小值,将最大值内移后的所有值]都成立
2.如果该二元组 > [最长边],则该条件对[固定二元组中较大值,将最小值内移后的所有值]都成立
三、代码
class Solution {
public:int triangleNumber(vector<int>& nums) {int n = 0;//组数sort(nums.begin(), nums.end());//排序 int Max_Val = nums.size() - 1;while(Max_Val >= 2)//默认只剩三个数时执行最后一次{int left = 0;int right = Max_Val - 1;while(left < right)//内层循环,每次确定最大边后,找二元组{if(nums[left] + nums[right] > nums[Max_Val]){n += (right - left);right--;}else{left++;}}Max_Val--;}return n;}
};LCR 179.查找总价值为目标值的两个商品
一、题目描述
OJ题目链接:力扣(LeetCode)
二、思路讲解
相信做过前一个题的朋友再做这题就感觉手到擒来了,这题我们也可以枚举,还可以用二分,但最好还是利用数组单调性使用双指针,从起止点开始计算,根据大小关系逐步排除起止点: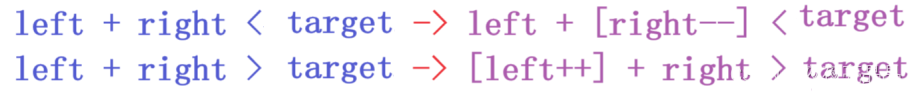
三、代码
class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int left = 0;int right = price.size() - 1;while(left < right){if(price[left] + price[right] > target)right--;else if(price[left] + price[right] < target)left++;else return {price[left], price[right]};//{}隐式类型转换}return {-1, -1};//LeetCode特色,末尾报错可以加}
};15.三数之和
一、题目描述
OJ题目链接:力扣(LeetCode)
二、思路讲解
与两数之和稍微不同的是,题⽬中要求找到所有「不重复」的三元组。那我们可以利⽤在两数之和
那⾥⽤的双指针思想,来对我们的暴⼒枚举做优化:
i. 先排序;
ii. 然后固定一个最大值 :
iii. 在这个数后⾯的区间内,使用「双指针算法」与最大值的和为0的二元组。
但是要注意的是,这道题里面需要有「去重」操作:
i. 找到⼀个结果之后, left 和 right 指针要「跳过重复」的元素;
ii. 当使用完⼀次双指针算法之后,固定的 a 也要「跳过重复」的元素
完成这些后,仍要注意细节操作:
谨防 vector 下标越界!!
三、代码
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums){vector<vector<int>> ret;sort(nums.begin(), nums.end());int Max_Val = nums.size() - 1;while (nums[Max_Val] >= 0 && Max_Val >= 1)//最大值如果小于0直接不用判断,Max_Val>=1//是为了防止Max_Val==0结束后自动的一次--{int left = 0;int right = Max_Val - 1;while (left < right){int sum = nums[left] + nums[right] + nums[Max_Val];if (sum > 0) right--;else if (sum < 0) left++;else{ret.push_back({ nums[left], nums[right], nums[Max_Val] });left++;right--;while (left < right && nums[left] == nums[left - 1]) left++;while (left < right && nums[right] == nums[right + 1]) right--;}}Max_Val--;//大while条件中Max_Val==0时要防止的--while (nums[Max_Val] == nums[Max_Val + 1] && Max_Val >= 1) Max_Val--;//Max_Val>=1仍是为了防止Max_Val==0结束后的一次--}return ret;}
};














:SingleChildScrollView、GridView)


)



