专栏导读
- 作者简介：工学博士，高级工程师，专注于工业软件算法研究
- 本文已收录于专栏：《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现，并提供所有案例完整源码；2.单元类型包含：杆单元，梁单元，平面三角形单元，薄板单元，厚板单元，壳单元，四/六面体实体单元，金字塔单元等；3.物理场问题涉及：力学、传热学、电磁学及多物理场耦合等问题的稳态（静力学）和瞬态（动力学）求解。专栏旨在帮助有志于有限元工业软件开发的小伙伴，快速上手有限元编程，在案例中成长，摆脱按部就班填鸭式教学。
- 【所有专栏文章均提供对应视频课】，文本教程+视频教程，双向强化学习！
- 欢迎订阅专栏，订阅用户可私聊进入有限元编程交流群（知识交流、问题解答），并获赠丰厚的有限元相关学习资料（教材、源码、视频课）
- 专栏订阅地址：有限元编程从入门到精通_suoge223的博客-CSDN博客
文章目录
专栏导读
文章目录
【总体简介】💻🔍
【代码截图】
【理论文本截图】
【视频教程】
【总体简介】💻🔍
本代码实现了二维悬臂梁结构的matlab有限元编程，涉及的梁单元类型有欧拉梁单元和铁木辛柯梁单元，实现上述两类梁单元静力分析求解，并针对铁木辛柯梁单元剪切自锁问题，开发了两种铁木辛柯梁单元，一种为完全积分的铁木辛柯梁，一种是减缩积分的铁木辛柯梁，并且对比了欧拉梁、铁木辛柯梁（完全积分）、铁木辛柯梁（减缩积分）的计算结果。
你将获得： 欧拉梁vs铁木辛柯梁matlab源码 + 理论文本
获取地址：Matlab梁单元有限元编程 | 铁木辛柯梁 | 欧拉梁 | Matlab源码 | 理论文本
代码运行的结果如下：
（1）L=5000,H=700,B=300的梁的计算结果
（2）L=5000,H=2700,B=300的梁的计算结果
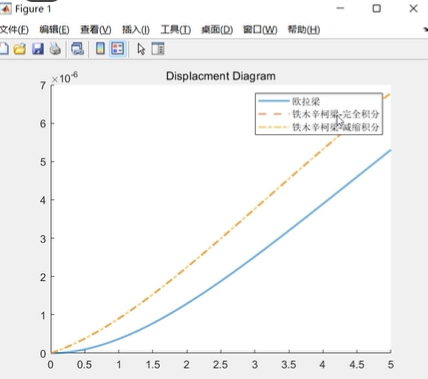
（3）L=5000,H=7,B=300的梁的计算结果
可见，对于（1）所示以弯曲变形为主的梁结构，三种单元均能给出一个较为准确的结果；对于（2）所示的深梁，剪切变形不可忽略，导致欧拉梁与铁木辛柯梁的计算结果相差较大，而且两种铁木辛柯梁均给出较精确的结果；对于（3）所示的扁梁，以受弯变形为主，因此欧拉梁和减缩积分的铁木辛柯梁均能给出合理结果，但是由于完全积分的铁木辛柯梁会发生严重的剪切自锁现象，因此与欧拉梁和减缩积分的铁木辛柯梁的结果相差较大。
【代码截图】
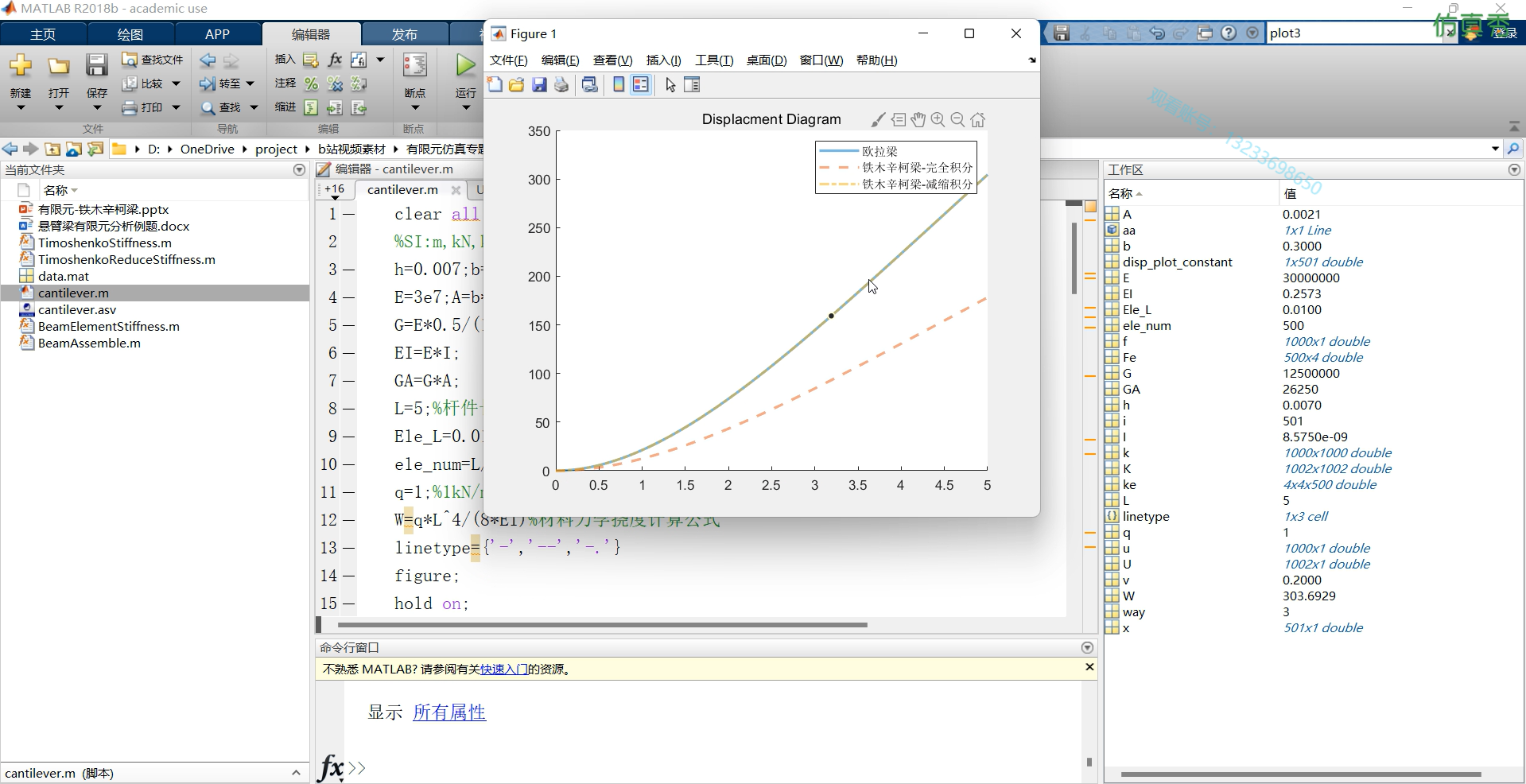
【理论文本截图】
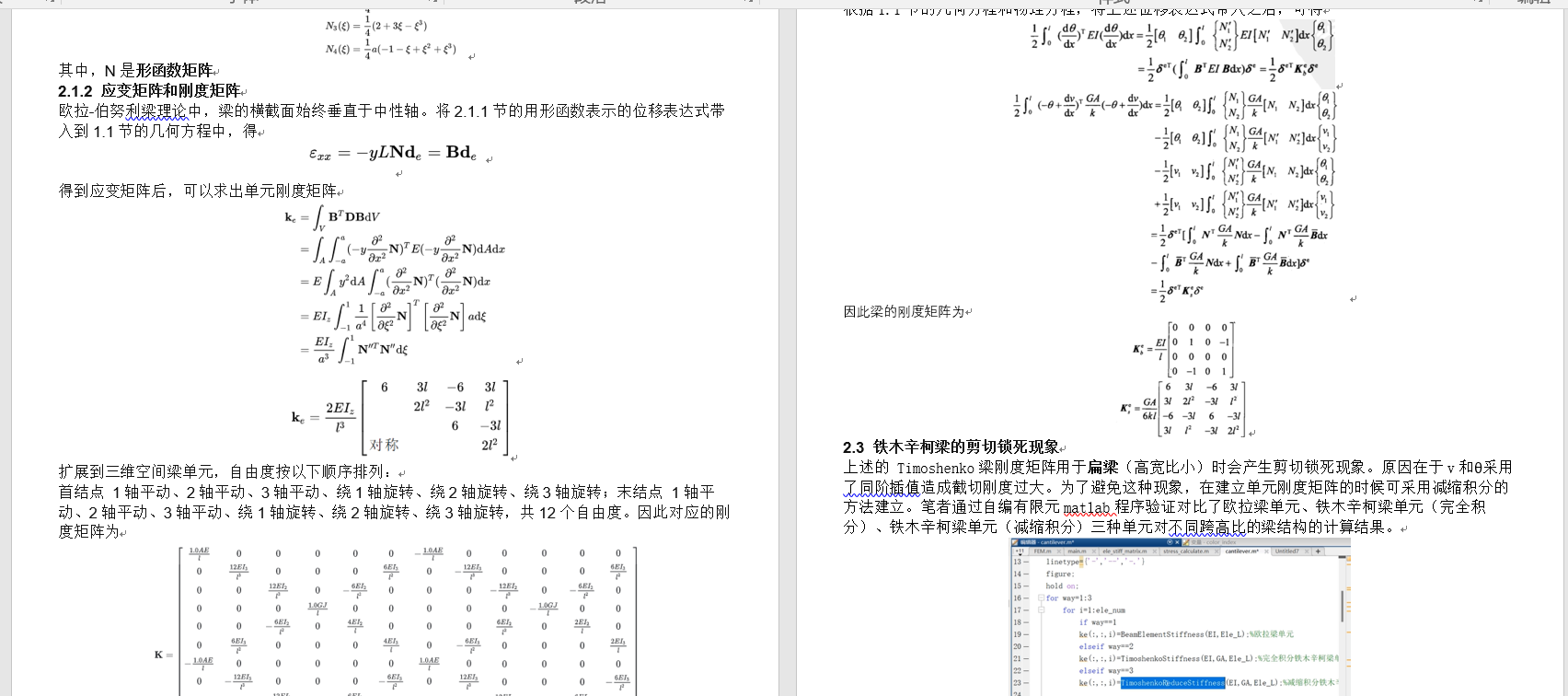
【视频教程】
【Matlab有限元编程从入门到精通/后处理/刚度矩阵/等参单元/高斯积分/Hammer积分/非线性/静力/动力/传热/三维/二维/梁板壳/实体/平面】 Matlab有限元编程从入门到精通/后处理/刚度矩阵/等参单元/高斯积分/Hammer积分/非线性/静力/动力/传热/三维/二维/梁板壳/实体/平面_哔哩哔哩_bilibili
)
