1.子集搜索与评价
对于1个学习任务来说,给定属性集,其中有些属性可能很关键、很有用,另一些属性则可能没什么用,我们将属性称为“特征”(feature),对当前学习任务有用的属性称为“相关特征”(relevant feature)、没什么用的属性称为“无关特征”(irrelevant feature).从给定的特征集合中选择出相关特征子集的过程称为“特征选择”(feature selection).
进行特征选择的原因:
有两个很重要的原因:
- 首先,我们在现实任务中经常会遇到维数灾难问题,这是由于属性过多而造成的,若能从中选择出重要的特征,使得后续学习过程仅需在一部分特征上构建模型,则维数灾难问题会大为减轻.
- 第二个原因是,去除不相关特征往往会降低学习任务的难度。
特征选择有两个环节,第一个环节是子集搜索,第二个环节是子集评价。
子集搜索是一种在特征选择中常用的策略,主要目的是从初始的特征集合中选取一个包含了所有重要信息的特征子集。这种策略的背景在于,当面对大量的特征时,如果直接对所有可能的特征子集进行遍历,可能会遭遇组合爆炸的问题,即需要评估的特征子集数量过于庞大,导致计算成本过高。
为了解决这个问题,子集搜索采用了一种贪心的策略。这种策略并不追求全局最优解,而是在每一步选择中都采取当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法。在特征选择中,这种贪心策略表现为每次从候选特征子集中选择出最优的一个或多个特征加入已选特征子集,或者从已选特征子集中删除最不重要的一个或多个特征。
子集搜索的具体实现方式有很多种,其中比较典型的有前向搜索和后向搜索。
- 前向搜索是从空集开始,逐渐添加特征到特征子集中,直到达到某个停止条件。
- 后向搜索则是从全集开始,逐渐删除特征,直到达到某个停止条件。
这两种搜索方式都可以根据评价函数的结果来调整特征子集的选择。
总的来说,子集搜索是一种有效的特征选择策略,它可以在降低计算成本的同时,尽可能地保留重要的特征信息。但是需要注意的是,由于贪心策略的存在,子集搜索可能会陷入局部最优解,而无法得到全局最优解。因此,在使用子集搜索时,需要根据具体的问题和数据情况来选择合适的搜索方式和评价函数。
子集评价可采用决策树的信息增益评价方法,即:
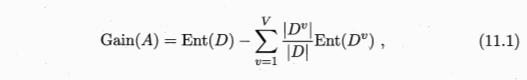
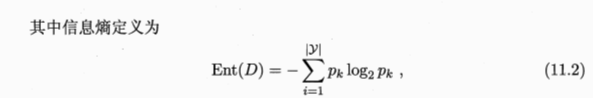
将特征子集搜索机制与子集评价机制相结合,即可得到特征选择方法.例如将前向搜索与信息熵相结合,这显然与决策树算法非常相似.事实上,决策树可用于特征选择,树结点的划分属性所组成的集合就是选择出的特征子集.其他的特征选择方法未必像决策树特征选择这么明显,但它们在本质上都是显式或隐式地结合了某种(或多种)子集搜索机制和子集评价机制.
常见的特征选择方法大致可分为三类: 过滤式(flter)、包式(wrapper)和嵌入式(embedding)
2.过滤式选择
过滤式方法先对数据集进行特征选择,然后再训练学习器,特征选择过程与后续学习器无关.这相当于先用特征选择过程对初始特征进行“过滤”,再用过滤后的特征来训练模型.
Relief是一种著名的过滤式特征选择方法,Relief算法设计了一个“相关统计量”来度量特征的重要性。这个统计量实际上是一个向量,它的每个分量都对应着一个特征,而该分量的值就代表着对应特征的重要性。对于数据集中的每个样例,Relief会首先找到与它同类别的最近邻样本(称为“猜中近邻”)和与它不同类别的最近邻样本(称为“猜错近邻”)。然后,基于这些近邻样本的信息,Relief会计算出每个特征的相关统计量分量。具体来说,对于某个特征,如果它与猜中近邻在该特征上的距离较小,而与猜错近邻在该特征上的距离较大,那么这个特征就被认为是重要的。

在实际应用中,可以根据相关统计量分量的大小来选择特征。例如,可以设定一个阈值,只选择那些相关统计量分量大于该阈值的特征;或者指定想要选择的特征个数k,然后选择相关统计量分量最大的k个特征。
Relief算法不仅适用于二分类问题,还可以通过扩展来处理多分类问题和回归问题。例如,针对多分类问题,可以为每个类别都找到对应的猜错近邻,并据此计算相关统计量;针对回归问题,可以考虑将目标属性视为连续值来处理。
3.包裹式选择
与过滤式特征选择不考虑后续学习器不同,包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价准则. 换言之包裹式特征选择的目的,就是为给定学习器选择最有利于其性能、“量身定做”的特征子集。
一般而言,由于包裹式特征选择方法直接针对给定学习器进行优化。因此从最终学习器性能来看,包裹式特征选择比过滤式特征选择更好,但另一方面,由于在特征选择过程中需多次训练学习器,因此包裹式特征选择的计算开销通常比过滤式特征选择大得多.
LVW(Las Vegas Wrapper)[Liu and Setiono,1996] 是一个典型的包裹式特征选择方法,它在拉斯维加斯方法(Las Vegas method)框架下使用随机策略来进行子集搜索,并以最终分类器的误差为特征子集评价准则。
4.嵌入式选择与L1正则化
嵌入式特征选择是一种将特征选择过程与学习器训练过程融为一体的方法,两者在同一个优化过程中完成,即在学习器训练过程中自动地进行了特征选择。这种方法有助于在学习过程中直接确定哪些特征对于模型的预测性能最为重要。
L1正则化是一种在损失函数中引入的范数,用于降低过拟合的风险。与L2范数相比,L1范数更易于获得“稀疏”解,即它求得的权重向量会有更少的非零分量。这种稀疏性意味着初始特征中仅有对应着非零权重的特征才会出现在最终模型中。因此,L1正则化可以被视为一种嵌入式特征选择方法,它在学习过程中自动地进行了特征选择。
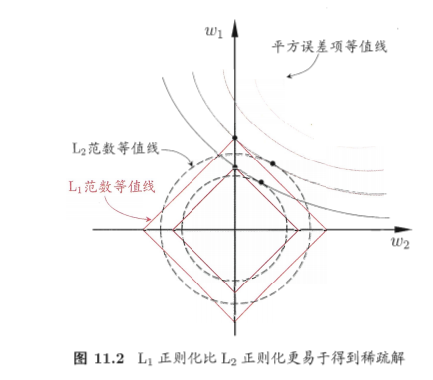
正如上图所示,L2正则化的超平面可以看做一个圆形,而L1可以看做一个菱形,L1正则化的最优解往往在坐标轴上取得,即分量为0。
5.稀疏表示与字典学习
当样本具有这样的稀疏表达形式时,对学习任务来说会有不少好处,例如线性支持向量机之所以能在文本数据上有很好的性能,恰是由于文本数据在使用上述的字频表示后具有高度的稀疏性,使大多数问题变得线性可分.同时,稀疏样本并不会造成存储上的巨大负担,因为稀疏矩阵已有很多高效的存储方法。
字典学习在稀疏表示中扮演着关键角色,其目标是从原始数据中构建一个过完备的字典(比原始数据空间更高维度),使得该字典能够稀疏地表示这些原始数据。这个字典是由一系列基本信号或原子组成的,这些原子可以视为数据空间中的基向量。原始信号则可以通过这些原子的线性组合来近似表示。
字典学习的过程实际上是一个优化问题,其核心思想是通过迭代优化算法不断更新字典和相应的稀疏表示,以达到最小化重构误差和满足稀疏性约束的目的。在这个过程中,重构误差反映了用字典中的原子线性组合来表示原始信号时的准确度,而稀疏性约束则要求这种表示尽可能简洁,即只有少量的原子被用于表示每个原始信号。
6.压缩感知
压缩感知在机器学习的理论中,可以被视为一种将经典机器学习理论与数据压缩技术结合的新兴方法,旨在提高机器学习的性能。这种方法主要利用信号在某个变换域上的稀疏性,通过选择合适的变换基进行信号的变换,使信号在该变换域上的表示变得稀疏。然后,通过较低的采样率对信号进行采样,获取较少的采样数据。最后,利用这些采样数据和信号在变换域上的稀疏表示,通过优化算法恢复原始信号。











:SingleChildScrollView、GridView)


)




