---

零、引例-小国王

1.问题描述

在 5×5 的棋盘里面放 K个国王，使他们互不攻击，共有多少种摆放方案。国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共 8 个格子。

2.暴力枚举

考虑到每个位置有放或不放两种情况，一共64个格子，那么有2^{64种情况，每种情况要遍历每一个位置判断是否合法，故而要计算2}25 * 25 = 838860800次，效率过于低下，考虑优化

3.多维dp

考虑到每一行放置方案和上一行都有关系，所以定义状态f(i, j, a, b, c, d, e)表示前i行放置j个国王，第i行放置情况为(a, b, c, d, e)分别代表第1、2、3、4、5列是否放国王，0代表不妨，1代表放

有转移方程：
$$f(i,j,a_i,b_i,c_i,d_i,e_i)=\sum f(i-1,j-a_i-b_i-c_i-d_i-e_i,a_{i-1},b_{i-1},c_{i-1},d_{i-1},e_{i-1})$$
当然上面的转移方程要满足规则限制，太过繁琐就略了（

这样的话一共5 * 5* 2^5 种状态，每次要从上一行的2^5的状态转移，每次要对a、b、c、d、e进行判断，一共计算5 * 5 * 2 ^ 5 * 2 ^ 5 * 5 = 640625次，时间复杂度大大降低

4.维度压缩

但是我们发现对于5*5的棋盘我们状态有7维，当棋盘增大，状态维度增加，太过于繁琐，有没有办法降维呢？

由于后五个维度只有0，1两种取值，所以可以将后五个维度看成二进制整数，换言之，一个位宽为5的二进制整数就能表示出后五个维度，二进制位第i位为1代表第i列放置国王，否则不放置

那么状态就压缩为了f[i][j][state]，比如f[3][5][10010]就代表前3行放置5个国王，第2行的第1、4列进行放置的方案数

---

一、状压dp

1.认识状压dp

动态规划就是在N维空间上进行递推的过程，每个维度看作一个节点，且只有0（尚未访问）和1（已访问）两个值。那么dp的过程就是从**（0，0，0，0，……0）到（1，1，1，1，……1）**的过程。

为了记录当前状态在每个维度上的坐标是0还是1，我们采用N位二进制数表示状态，即用[0, 2 ^ N - 1]的十进制整数存储节点的访问情况。为了记录最后经过的节点是哪一个，我们用节点编号作为附加信息，也记录在dp的状态中，这样我们就得到了由N和2^N大小两个维度构成的状态数组f[N][1 << N]。

常见的状压dp大致可以分为棋盘式（基于连通性）和集合型两类。

---

2.棋盘式(基于连通性)

棋盘式通常会给出n*m的矩阵，然后格子占用的规则，一般表现为同行的不同列间的限制以及和前面若干行的限制。我们可以用位长m的二进制整数来表示出一行各列的放置情况，然后根据规则初始化状态数组，进行状态转移。

---

2.1小国王

2.1.1题目链接

[P1896 SCOI2005] 互不侵犯 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

2.1.2思路分析

显然可以用n位二进制整数表示出一行的放置情况

在不考虑和其他行冲突的情况下，有效状态state满足((state << 1) & state) = 0，即无同行相邻国王

那么可以O(2^n)预处理出所有的同行有效状态，顺便计算每个状态的1的个数sum

然后定义状态数组，f[i][j][state]代表前i行放置j个国王且第i行状态为state的方案数

那么有状态转移方程：
$$\begin{gathered} f[i][j][a]=\sum f[i-1][j-c][b] \\ 其中a\&b=0,(a<<1)\&b=0,(a>>1)\&b=0,c=sum(a) \end{gathered}$$
显然有初始状态f[0][0][0] = 1，空棋盘方案为1

然后把转移方程翻译成代码即可，为了方便我们计算到n + 1行的状态，这样f[n + 1][k][0]即为答案

2.1.3AC代码

#include <iostream>
using namespace std;
#define int long long
const int N = 11, M = N * N + 5;
int f[N][M][1 << N], state[1 << N], sum[1 << N];
int n, k, tot = 0;
signed main()
{//freopen("in.txt", "r", stdin);ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n >> k;for (int i = 0, ed = (1 << n); i < ed; i++)if (!(i & (i << 1)))state[tot] = i, sum[tot++] = __builtin_popcount(i);f[0][0][0] = 1;for (int i = 1; i <= n + 1; i++)for (int j = 0; j <= k; j++)for (int a = 0; a < tot; a++)for (int b = 0, c = sum[a]; b < tot; b++){if (j >= c && !(state[a] & state[b]) && !(state[a] & (state[b] << 1)) && !(state[a] & (state[b] >> 1)))f[i][j][a] += f[i - 1][j - c][b];}cout << f[n + 1][k][0];return 0;
}

2.2玉米田

2.2.1题目链接

[P1879 USACO06NOV] Corn Fields G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

2.2.2思路分析

在不考虑废弃玉米田和其他行限制的情况下，同行有效状态state满足:state << 1 & state = 0

那么同样的，我们预处理出同行的所有有效状态states

然后每一行的废弃玉米田都会对同行状态造成限制，我们开一个数组g[]，g[i]也是一个n位二进制整数，第i行废弃玉米田格子对应位被置1，这样我们选择第i行状态的时候要满足state & g[i] = 0

定义状态数组f[][]，f[i][j]代表前i行完成种植且第i行状态为j的最大方案数

有状态转移方程：
$$f[i][j]=\sum f[i-1][k],其中j\&k=0且j\&g[i]=0$$
初始状态f[0][0] = 1，然后翻译转移方程为代码，同样计算到n + 1行，f[n+1][0]即为答案

2.2.3AC代码

#include <iostream>
using namespace std;
#define int long long
const int N = 14, M = N * N + 5, mod = 1e8;
int m, n, tot = 0;
int f[N][1 << N]{0}, states[1 << N], g[N];
signed main()
{freopen("in.txt", "r", stdin);ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> m >> n;for (int i = 1; i <= m; i++)for (int j = 0, t; j < n; j++)cin >> t, g[i] |= ((!t) << j);for (int i = 0, ed = (1 << n); i < ed; i++)if (!(i & (i << 1)))states[tot++] = i;f[0][0] = 1;for (int i = 1; i <= m + 1; i++)for (int j = 0; j < tot; j++)for (int k = 0; k < tot; k++)if (!(states[j] & g[i]) && !(states[j] & states[k]))f[i][j] = (f[i][j] + f[i - 1][k]) % mod;cout << f[m + 1][0];return 0;
}

2.3炮兵阵地

2.3.1题目链接

[P2704 NOI2001] 炮兵阵地 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

2.3.2思路分析

和前两道不同的地方就是，每一行会受到相邻两行的限制，但是换汤不换药，我们按照之前的思路来即可

同样先预处理同行有效状态states，以及有效状态对应1的数目cnt

然后根据每行的地形，预处理出g[]，g[i]为m位二进制整数，山地对应位置一

定义状态数组f[i][j][k]，代表前i行布置完毕，第i - 1行状态为k，第i行状态为j

那么有状态转移方程:
$$f[i][j][k]=max(f[i-1][k][x])+cnt[j]，j,k,x两两相与为0，j\&g[i]=k\&g[i-1]=0$$
初始状态都是0，不用初始化

翻译递推为代码，处理到n+2行，这样答案就是f[n+2][0][0]

考虑节省空间，我们滚动数组优化，最终答案就是f[(n+2)&1][0][0]

2.3.3AC代码

#include <iostream>
using namespace std;
#define int long long
const int N = 103, M = 11, mod = 1e8;
int m, n, tot = 0;
int g[N], states[1 << M], cnt[1 << M], f[2][1 << M][1 << M];signed main()
{//freopen("in.txt", "r", stdin);ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n >> m;for (int i = 1; i <= n; i++)for (int j = 0; j < m; j++){char ch;cin >> ch;g[i] |= ((ch == 'H') << j);}for (int i = 0, ed = 1 << m; i < ed; i++)if ((i & (i >> 1)) || (i & (i >> 2)))continue;elsestates[tot] = i, cnt[tot++] = __builtin_popcount(i);for (int i = 1; i <= n + 2; i++)for (int j = 0; j < tot; j++)for (int k = 0; k < tot; k++)for (int x = 0; x < tot; x++){int a = states[j], b = states[k], c = states[x];if ((a & b) || (b & c) || (a & c))continue;if ((a & g[i]) || (b & g[i - 1]))continue;f[i & 1][j][k] = max(f[(i - 1) & 1][k][x] + cnt[j], f[i & 1][j][k]);}cout << f[(n + 2) & 1][0][0];return 0;
}

2.4蒙德里安的梦想

2.4.1题目链接

291. 蒙德里安的梦想 - AcWing题库

2.4.2思路分析

先明确一点：横放方案数=竖放方案数=总方案数，因为对于一种方案只要横放确认了，那么剩下的都是竖放

和前面不同，我们考虑按列放置

如果格子被竖向覆盖或者横向终点覆盖，置0，被横向起点覆盖置1

如：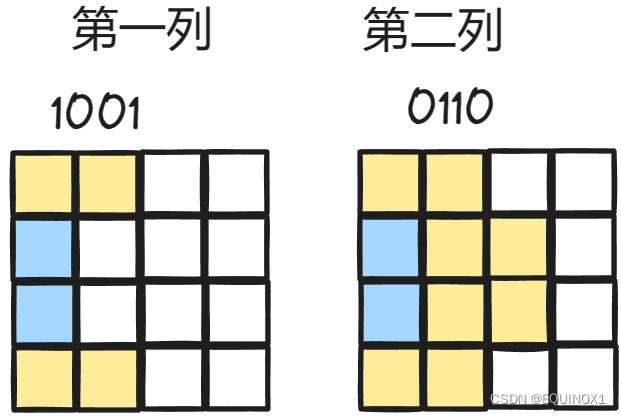

我们定义状态f[i][j]代表放完前i列，第i列状态为j的方案数

那么f[i][j]可以由f[i - 1][]转移，初始有f[0][0] = 1，其它都是0

我们最终答案应该是f[m][0]，因为最后一列无法作为横放起点

和前面不同，前面都是预处理同行合法状态，这里预处理合并两列合法状态，如：

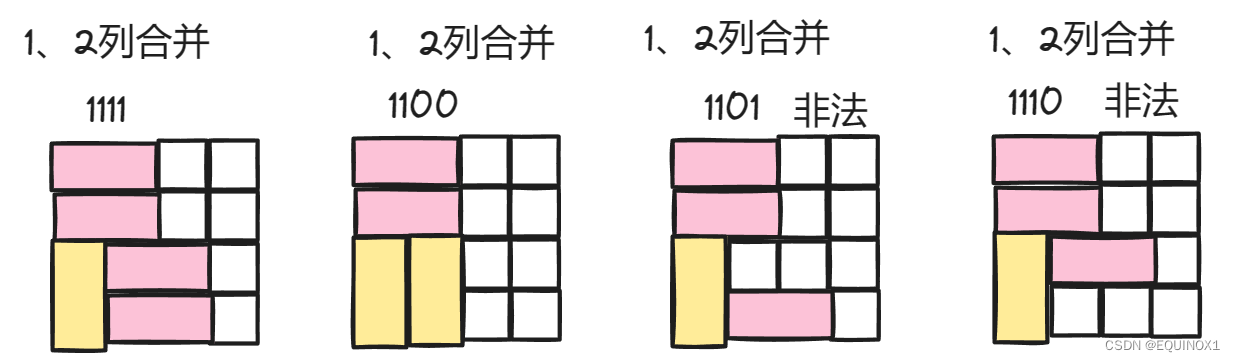
不难看出，两列合并即做或运算

而如果两列合并后有连续的奇数个0，说明非法

那么我们可以预处理出所有状态是否有连续奇数0的情况even,even[i] = 1说明没有

然后对于两列状态，显然要满足i & j = 0，如果不为0，说明有重合的横放

这样有状态转移方程
$$f[i][j]=\sum f[i-1][k]，even[i\&j]=1且i\&j=0$$
翻译成代码即可，最终输出f[m][0]
相对于前三题，这道题状态不好想

2.4.3AC代码

#include <iostream>
#include <iostream>
#include <algorithm>
#include <cstring>
#define int long long
using namespace std;
const int N = 12, M = 12;
int n, m;
int f[M][1 << N];
bool even[1 << N];
signed main()
{//freopen("in.txt", "r", stdin);ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);while (cin >> n >> m, n && m){memset(f, 0, sizeof f), memset(even, 0, sizeof even);for (int i = 0, ed = (1 << n), cnt = 0; i < ed; i++){cnt = 0, even[i] = 1;for (int j = 0; j < n; j++)if ((1 << j) & i){if (cnt & 1){even[i] = 0;break;}}elsecnt++;if (cnt & 1)even[i] = 0;}f[0][0] = 1;for (int i = 1; i <= m; i++){for (int j = 0, ed = (1 << n); j < ed; j++)for (int k = 0, ed = (1 << n); k < ed; k++)if (!(j & k) && even[j | k])f[i][j] += f[i - 1][k];}cout << f[m][0] << '\n';}return 0;
}

---

3.集合

集合型问题，一般根据每个元素选或不选，用二进制整数表示集合内元素选取状况来作为状态。根据集合内元素是否可重复使用可以分为重复覆盖问题和不可重复覆盖问题（当然这在舞蹈链中也有涉及）。

3.1 递归实现指数型枚举

3.1.1题目链接

92. 递归实现指数型枚举 - AcWing题库

3.1.2思路分析

每个数字都有选或不选两种情况，那么我们用n位二进制整数表示集合内元素选取情况即可

把[0, (1 << n) - 1]遍历一遍即可

3.1.3AC代码

#include<iostream>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
bool vis[16]{0};
int n;
void dfs(int x, int state){if(x == n){for(int i = 0; i < n; i++)if(state & (1 << i))cout << i + 1 << ' ';cout << '\n';return;}dfs(x + 1, state), dfs(x + 1, state | (1 << x));
}
int main(){ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n;dfs(0, 0);return 0;
}

3.2最短Hamilton路径

3.2.1题目链接

91. 最短Hamilton路径 - AcWing题库

3.2.2思路分析

哈密顿路径问题是集合类状压dp中一个非常经典的问题，因为很多问题都能抽象成图模型，继而转化为哈密顿路径问题

哈密顿路径要求路径遍历所有点且只一次，显然是不可重复覆盖问题。

那么我们考虑用n位二进制整数表示当前路径包含的点

接下来就是设计状态，因为我们状压dp的状态一般要获取最后一步的位置，所以定义状态f[i][j]为从0出发当前路径状态为i且终点为j的最短距离

那么有状态转移方程：
$$f[i][j]=min(f[i][j],f[a][b]+g[b][j])，其中i>>j\&1$$
由于题目要求起点为0，所以初始状态f[1][0] = 0

写代码时有个优化就是因为要求从0出发所以有效状态满足i & 1

3.2.3AC代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define int long long
const int N = 20;
int n, g[N][N]{0}, f[1 << N][N];
signed main(){ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n;for(int i = 0; i < n; i++)for(int j = 0; j < n; j++)cin >> g[i][j];memset(f, 0x3f, sizeof f);f[1][0] = 0;for(int i = 0, ed = 1 << n; i < ed; i++)if(i & 1)for(int j = 0; j < n; j++)if(i >> j & 1)for(int k = 0; k < n; k++)if(i >> k & 1)f[i][j] = min(f[i][j], f[i ^ (1 << j)][k] + g[k][j]);cout << f[(1 << n) - 1][n - 1];return 0;
}

3.3毕业旅行问题

3.3.1题目链接

731. 毕业旅行问题 - AcWing题库

3.3.2思路分析

和哈密顿路径问题几乎一样

我们计算出从0出发的哈密顿路径最短距离后，取所有点为终点的哈密顿路径长度加上终点到起点距离中最小的那个即可

3.3.3AC代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
//#define int long long
const int N = 20;
int n, f[1 << N][N], g[N][N];
signed main(){ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n;for(int i = 0; i < n; i++)for(int j = 0; j < n; j++)cin >> g[i][j];memset(f, 0x3f, sizeof f), f[1][0] = 0;for(int i = 0, ed = 1 << n; i < ed; i++)if(i & 1)for(int j = 0; j < n; j++)if(i >> j & 1)for(int k = 0; k < n; k++)if(i >> k & 1)f[i][j] = min(f[i][j], f[i ^ (1 << j)][k] + g[k][j]);int ret = 0x3f3f3f3f;for(int i = 1; i < n; i++)ret = min(ret, f[(1 << n) - 1][i] + g[i][0]);cout << ret;return 0;
}

3.4 愤怒的小鸟

3.4.1题目链接

524. 愤怒的小鸟 - AcWing题库

3.4.2思路分析

状压dp的题很多时候是根据数据范围来推测用状压dp的，然后往那边靠

对于这个题目而言，每个坐标就是一个元素，抛物线方程中有两个未知数，所以任意两点确定一条抛物线，当然要去掉开口朝上和竖直线的情况

这样我们O(n^2)与处理出path[x][y]，path[x][y]为n位二进制整数即代表xy所在抛物线穿过点的状态，处理方法就是确定曲线合法后遍历所有点判断该点是否在曲线上

然后定义状态f[i]代表选取集合状态为i时所用最少曲线数目

对于f[i]，我们如果思考它可以由哪个状态转移而来的话太过困难

所以我们可以这样进行状态转移

对于状态i，从低到高枚举找到第一个未被包含的位x，然后有：
$$f[i|path[x][j]]=min(f[i|path[x][j]],f[i]+1)$$
代码实现时候，注意浮点数精度的处理

3.4.3AC代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define int long long
typedef pair<double, double> PDD;
const int N = 18, M = 1 << N, mod = 1e8;
const double eps = 1e-8;
int n, m;
int f[M], path[N][N];
PDD points[N];
int cmp(double x, double y)
{if (fabs(x - y) < eps)return 0;return x > y ? 1 : -1;
}
void solve()
{cin >> n >> m;for (int i = 0; i < n; i++)cin >> points[i].first >> points[i].second;memset(path, 0, sizeof path), memset(f, 0x3f, sizeof f), f[0] = 0;for (int i = 0; i < n; i++){double x1 = points[i].first, y1 = points[i].second;path[i][i] = 1 << i;for (int j = 0; j < n; j++){double x2 = points[j].first, y2 = points[j].second;if (!cmp(x1, x2))continue;double a = (y1 / x1 - y2 / x2) / (x1 - x2), b = y1 / x1 - a * x1;if (cmp(a, 0) >= 0)continue;int state = 0;for (int k = 0; k < n; k++){double x = points[k].first, y = points[k].second;if (!cmp(a * x * x + b * x, y))state |= (1 << k);}path[i][j] = state;}}for (int i = 0; i + 1 < 1 << n; i++){int x = 0;for (int j = 0; j < n; j++){if (!((1 << j) & i)){x = j;break;}}for (int j = 0; j < n; j++)f[i | path[x][j]] = min(f[i] + 1, f[i | path[x][j]]);}cout << f[(1 << n) - 1] << '\n';
}
signed main()
{//freopen("in.txt", "r", stdin);ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int _ = 1;cin >> _;while (_--)solve();return 0;
}