BFS基本模版与案例可以参考:
【LeetCode每日一题】【BFS模版与例题】863.二叉树中所有距离为 K 的结点
【LeetCode每日一题】【BFS模版与例题】【二维数组】130被围绕的区域 && 994 腐烂的橘子

思路:
-
特殊情况:
最短的路径是向下再向右,在这条路径上最多有经过row+col-1个位置,除去起点、终点,最多可以有row+col-3个阻碍,如果k>=row+col-3 ,则证明说,走最短路径,即使有row+col-3个阻碍,也都能移除。 -
对于不考虑可以越过障碍物的常规情况,经过的每一个点都可以用【x,y】来表示,无论走那一条路径经过该点,都可以用【x,y】表示。
-
对于此题,点坐标【x,y】不足以与表示一个点的情况:显然即使在同一位置上,可以越过障碍的剩余机会数目也会决定之后是否能走完、可以走的最短路径等信息,所以需要【x,y,rest】三元组来与当前状态一一对应。比如下图,k = 1 的情况,在【2,0】这个位置,通过橙色路线经过时,已经无法到达终点,但是通过绿色路线经过时仍然可以到达终点。因此,【2,0】这个位置还需要记录当前剩余的特权次数!
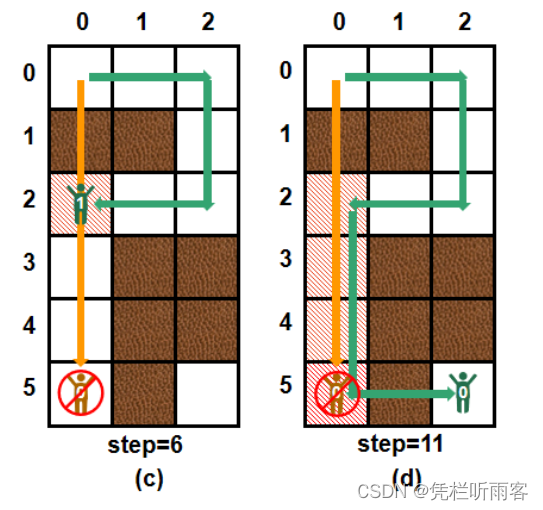
图片来源:添加链接描述
var shortestPath = function (grid, k) {let row = grid.lengthlet col = grid[0].length// 特殊情况1:if(row === 1 && col === 1) return 0// 特殊情况2:最短的路径是row-1+col-1,在这条路径上最多有经过row+col-1个位置,除去起点、终点,最多可以有row+col-3个阻碍if (k >= row + col - 3) {return row + col - 2}let step = 0let queue = [[0, 0, k]]let visited = new Set()visited.add(`${0},${0},${k}`)while (queue.length) {let size = queue.lengthstep++for (let i = 0; i < size; i++) {let [x, y, remainder] = queue.shift()// 上下左右const distance = [[-1, 0],[1, 0],[0, -1],[0, 1]]// 遍历临近的节点for (let j = 0; j < distance.length; j++) {const [dx, dy] = distance[j]let nextX = dx + xlet nextY = dy + yif (nextX < 0 || nextX >= row || nextY < 0 || nextY >= col) {continue}if (grid[nextX][nextY] === 0 &&!visited.has(`${nextX},${nextY},${remainder}`)) {// 满足条件时返回stepif (nextX === row - 1 && nextY === col - 1) {return step}queue.push([nextX, nextY, remainder])visited.add(`${nextX},${nextY},${remainder}`)}if (grid[nextX][nextY] === 1 &&remainder > 0 &&!visited.has(`${nextX},${nextY},${remainder - 1}`)) {queue.push([nextX, nextY, remainder - 1])visited.add(`${nextX},${nextY},${remainder - 1}`)}}}}return -1
}







linux 块设备驱动)


设置主题续2)


)

)



)