✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
🌟🌟 追风赶月莫停留 🌟🌟
🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀
🌟🌟 平芜尽处是春山🌟🌟
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅

🍑二叉树

🍍二叉树的含义

二叉树是一种树形结构，其特点是每个节点最多有两个子树。

二叉树是一种有序树，这意味着它的子树按照一定的顺序排列，通常左子树出现在右子树之前。二叉树的递归定义可以描述为：二叉树可以是空的，也可以由一个根节点和两个互不相交的子树组成，这两个子树分别称为左子树和右子树。左子树和右子树自身也构成二叉树。

🍍二叉树的结构

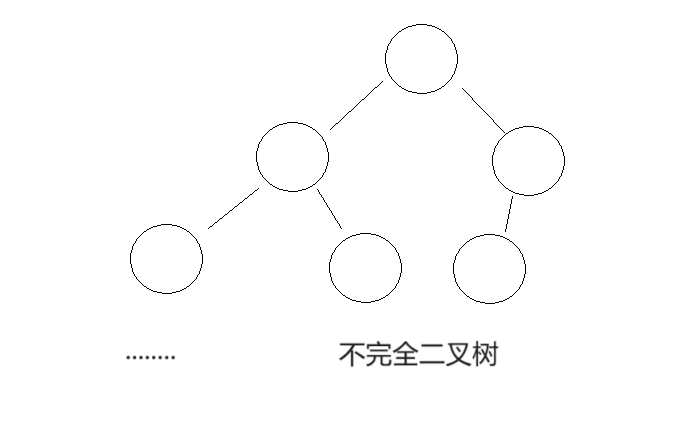
现实中的二叉树：

现实中的树，就是我们学过的二叉树倒过来的样子，大家可以把手机屏幕倒过来看试试。

🍍二叉树的存储结构

二叉树分为顺序存储和链式存储

顺序存储：类似于数组的存储形式，但只有完全二叉树才会用顺序存储，这样才不会造成空间的浪费

链式存储：利用了链表的性质。每个节点都存储了上个树和下个树的位置，这也就是带头指针的双链表结构

🍑堆

🍍堆的含义

堆是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：
（1）堆中某个结点的值总是不大于或不小于其父结点的值；
（2）堆总是一棵完全二叉树。
（3）将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。常见的堆有 二叉堆、斐波那契堆等。
（4）堆的物理结构本质上是顺序存储的，是线性的。但在逻辑上不是线性的，是完全二叉树的这种逻辑储存结构。 堆的这个数据结构，里面的成员包括一维数组，数组的容量，数组元素的个数，有两个直接后继。

🍍堆的结构

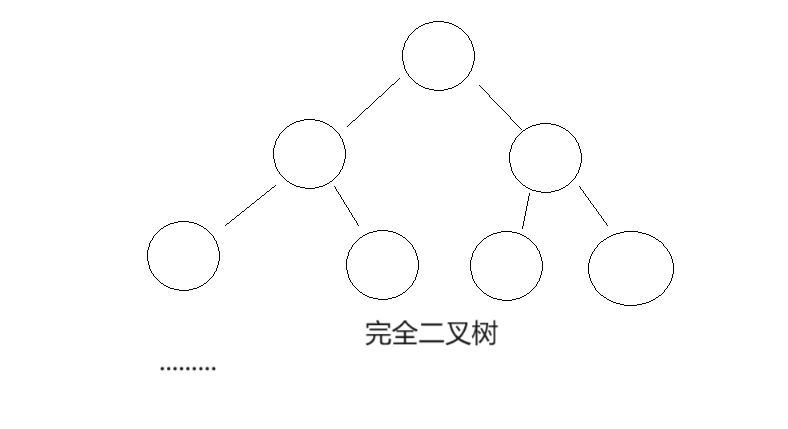
堆的结构就是特殊的二叉树结构，也就是上图中完全二叉树的样子

🍍堆的实现

堆的实现又分为大堆和小堆
大堆：任何父节点都大于等于子节点。
小堆：任何父节点都小于等于子节点。
两个子节点之间的大小没有明确规定

🍌补充条件

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int HPDatetype;
typedef struct Heap
{HPDatetype* a;int catacity;int size;
}HP;void Swap(HPDatetype *a1, HPDatetype *a2)
{HPDatetype cur = *a1;*a1 = *a2;*a2 = cur;
}

Swap（）函数是交换两个数的作用，是利用结构体形式创建的堆

🍌堆的初始化

void HeapInia(HP* ps)
{assert(ps);//防止堆为空ps->a = NULL;ps->size = ps->catacity = 0;
}

🍌堆的销毁

void HeapDestroy(HP* ps)
{assert(ps);//防止堆为空free(ps->a);ps->a = NULL;ps->size = 0;ps->catacity = 0;
}

🍌堆的插入

void AdjustUp(HPDatetype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HeapPush(HP* ps, HPDatetype x)
{assert(ps);//防止堆为空if (ps->catacity == ps->size){if (ps->catacity == 0){ps->catacity = 2;}else{ps->catacity *= 2;}int newcatacity = ps->catacity;HPDatetype* cur = (HPDatetype*)realloc(ps->a, sizeof(HPDatetype) * newcatacity);if (cur == NULL){perror("realloc fail");exit(-1);}ps->a = cur;ps->catacity = newcatacity;}ps->a[ps->size] = x;(ps->size)++;AdjustUp(ps->a, ps->size - 1);
}

AdjustUp（）函数是把子节点向上调整的作用，因为我们利用数组形式建立堆，只能分为大堆和小堆，所以需要重新设计一个函数来调整子节点的位置。在这里我们是创建小堆。关于怎么向上找父节点，是利用了数组的位置特性。数组是从0开始，大家就可以找规律，以父节点找子节点就是需要加1再除以2，以子节点找父节点就是减1除以2。

🍌 堆的删除

void AdjustLown(HPDatetype* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* ps)
{assert(ps);assert(ps->size > 0);Swap(&(ps->a[0]), &(ps->a[ps->size - 1]));(ps->size)--;AdjustLown(ps->a, ps->size, 0);//向下调整}

堆的删除，在这里我们是删除的堆顶数据。
首先我们是先把堆顶数据和堆尾数据交换，然后再删除堆顶数据，最后利用函数AdjustLown()进行向下调整就行。
如果是小堆，取出来的数据就是依次变大，相反是大堆，取出来的数据就是依次变小。
堆在这里还有一个应用，就是堆排序。小堆就是升序，大堆就是降序。

🍌取堆顶的数据

HPDatetype HeapTop(HP* ps)
{assert(ps);assert(ps->size > 0);return ps->a[0];
}

返回堆顶数据即可

🍌堆的数据个数

int HeapSize(HP* ps)
{return ps->size;
}

直接返回ps->size即可

🍌堆的判空

bool HeapEmpty(HP* ps)
{assert(ps);return ps->size == 0;
}

注意，这里判空用到bool需要头文件名#include<stdbool.h>

🍌堆的整体代码实现

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int HPDatetype;
typedef struct Heap
{HPDatetype* a;int catacity;int size;
}HP;void HeapInia(HP* ps)
{assert(ps);ps->a = NULL;ps->catacity = ps->size = 0;
}void HeapDestroy(HP* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->size = ps->catacity;
}void Swap(HPDatetype* a1, HPDatetype* a2)
{HPDatetype cur = *a1;*a1 = *a2;*a2 = cur;
}void AdjustUp(HPDatetype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HeapPush(HP* ps, HPDatetype x)
{assert(ps);if (ps->size == ps->catacity){if (ps->catacity == 0)ps->catacity = 2;elseps->catacity *= 2;int newcatacity = ps->catacity;HPDatetype* cur = (HPDatetype*)realloc(ps->a, sizeof(HPDatetype) * newcatacity);if (cur == NULL){perror("realloc fail");exit(-1);}ps->a = cur;ps->catacity = newcatacity;}ps->a[ps->size] = x;(ps->size)++;AdjustUp(ps->a, ps->size - 1);}void AdjustLown(HPDatetype* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* ps)
{assert(ps);assert(ps->size > 0);Swap(&(ps->a[0]), &(ps->a[ps->size - 1]));(ps->size)--;AdjustLown(ps->a, ps->size, 0);}HPDatetype HeapTop(HP* ps)
{assert(ps);assert(ps->size > 0);return ps->a[0];
}int HeapSize(HP* ps)
{return ps->size;
}bool HeapEmpty(HP* ps)
{assert(ps);return ps->size == 0;
}void HeapPrint(HP *ps)
{for (int i = 0; i < ps->size; i++){printf("%d ", ps->a[i]);}printf("\n");
}int main()
{int a[] = { 65,100,70,32,50,60 };int size = sizeof(a) / sizeof(a[0]);HP ps;HeapInia(&ps);for (int i = 0; i < size; i++){HeapPush(&ps, a[i]);}HeapPrint(&ps);int net = HeapSize(&ps);//堆排序while (!HeapEmpty(&ps)){printf("%d ", HeapTop(&ps));HeapPop(&ps);}printf("%d ", net);HeapDestroy(&ps);return 0;
}

上面我也不充了堆排序，大家有兴趣可以试试，由于我这里是建的小堆，所以排出来的序是升序。

有不足的地方欢迎大家指正,谢谢！！！