目录
🎂最大子数组和
O(n) 暴力
O(n) 动态规划
🚩合并区间
O(nlogn) 排序
🌼轮转数组
O(n) 辅助数组
O(n) 环状替换
O(n) 数组翻转
🌼除自身以外数组的乘积
O(n) 前缀和
时间O(n) 空间O(1)
🌙缺失的第一个正数
O(n) 哈希
O(n) 哈希 + 空间优化(标记)
O(n) 置换
🎂最大子数组和
53. 最大子数组和 - 力扣(LeetCode)
O(n) 暴力
边加边判断,是否可以更新当前子数组和 && 最大值
class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();int Max = -1e4, sum = 0;for (int i = 0; i < n; ++i) {sum += nums[i];Max = max(Max, sum);if (sum < nums[i]) { // 子数组和 < 当前值sum = nums[i]; // 更新子数组和Max = max(Max, sum); // 更新最大值}}return Max;}
};O(n) 动态规划
看注释
代码1
class Solution {
public:int maxSubArray(vector<int>& nums) {const int n = nums.size();int dp[n + 1];dp[0] = nums[0];for (int i = 1; i < n; ++i) dp[i] = max(nums[i], dp[i - 1] + nums[i]);int ans = -1e4;for (int i = 0; i < n; ++i)ans = max(ans, dp[i]);return ans;}
};
/*
1,含义:dp[i] 索引 i 结尾的最大值
2,递推:dp[i] = max(dp[i - 1] + nums[i], nums[i]) 可以连续 或 重新开始
3,初始化:dp[0] = nums[0]
4,遍历顺序:前往后
5,打表检验
*/代码2
滚动数组的想法,将一维数组优化成变量
class Solution {
public:int maxSubArray(vector<int>& nums) {int sum = 0, ans = -1e4;for (auto x : nums) {sum = max(sum + x, x); // 可以连续 或 重新开始ans = max(ans, sum);}return ans;}
};
🚩合并区间
56. 合并区间 - 力扣(LeetCode)
O(nlogn) 排序
复习下 vector
vector<int>a;
vector<int>a(100); //元素个数100,所有数初值为0
vector<int>a(10, 666); //元素个数100,所有数初值为666
vector<int>b(a); //b是a的复制
vector<int>b(a.begin()+3, a.end()-3); //复制[a.begin()+3, a.end()-3)区间元素到vectorvector<int>a[5]; //创建了5个vector, 每个都是一个数组a.push_back(5); //尾插一个元素5
a.insert(a.begin()+1, 10); //在a.begin()+1指向元素前插入10
a.insert(a.begin()+1, 5, 10); //a.begin()+1前插入5个10
a.insert(a.begin()+1, b.begin(), b.begin()+3); //a.begin()+1前插入b向量区间元素a.pop_back(); //删除向量最后一个元素
a.erase(a.begin()+1); //删除指定位置元素
a.erase(a.begin()+3, a.end()-3); //删除区间[first, last)的元素
a.clear(); //清空向量for(int i = 0; i < a.size(); ++i)cout<<a[i]<<"\t";
for(vector<int>::iterator it = a.begin(); it < a.end; ++it)cout<<*it<<"\t";容器通用函数
.size() //元素个数
.empty() //为空,返回bool值
.front() //第一个元素
.back() //最后一个元素
.begin() //指向第1个的指针
.end() //指向最后1个的指针
.swap(b) //交换两个容器内容
::iterator //迭代器注意,sort(.begin(), .end()),默认第一个元素升序,第一个元素相同,就按第二个元素升序,
我还写了个例子验证👇
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;int main() {vector<vector<int>> intervals = {{1, 3}, {2, 6}, {1, 5}, {1, 2}, {3, 7}, {4, 9}, {1, 8}, {5, 6}, {1, 1}, {7, 8},{1, 4}, {2, 2}, {1, 6}, {3, 4}, {1, 9}, {2, 8}, {1, 7}, {4, 5}, {1, 10}, {3, 3}};// 使用 sort(begin, end) 对二维数组进行排序,先按第一个元素升序,再按第二个元素升序sort(intervals.begin(), intervals.end());// 输出排序后的结果for (const auto& interval : intervals) {cout << "[" << interval[0] << ", " << interval[1] << "]" << endl;}return 0;
}
[1, 1]
[1, 2]
[1, 3]
[1, 4]
[1, 5]
[1, 6]
[1, 7]
[1, 8]
[1, 9]
[1, 10]
[2, 2]
[2, 6]
[2, 8]
[3, 3]
[3, 4]
[3, 7]
[4, 5]
[4, 9]
[5, 6]
[7, 8]思路
先排序,已知 sort() 根据每个 vector 第一个元素升序,第一个相同就第二个升序(字典序)
然后 for 循环遍历 O(n)
如果 ans[][] 为空 或 ans[][] 最后一个数组 [l, r] 的右边界 r,小于 intervals[][] 当前数组的左边界
说明没有交集,直接插入
反之,如果有交集,就取两个右边界的最大值
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {vector< vector<int> > ans; // 二维数组存答案int n = intervals.size();sort(intervals.begin(), intervals.end()); // 第一元素升序,第一相同按第二元素for (int i = 0; i < n; ++i) {int l = intervals[i][0], r = intervals[i][1]; // 左右边界if (ans.empty() || ans.back()[1] < l) // 没有交集ans.push_back({l, r}); // 直接插入else // 有交集,答案数组右边界 = 较大值ans.back()[1] = max(ans.back()[1], r);}return ans;}
};🌼轮转数组
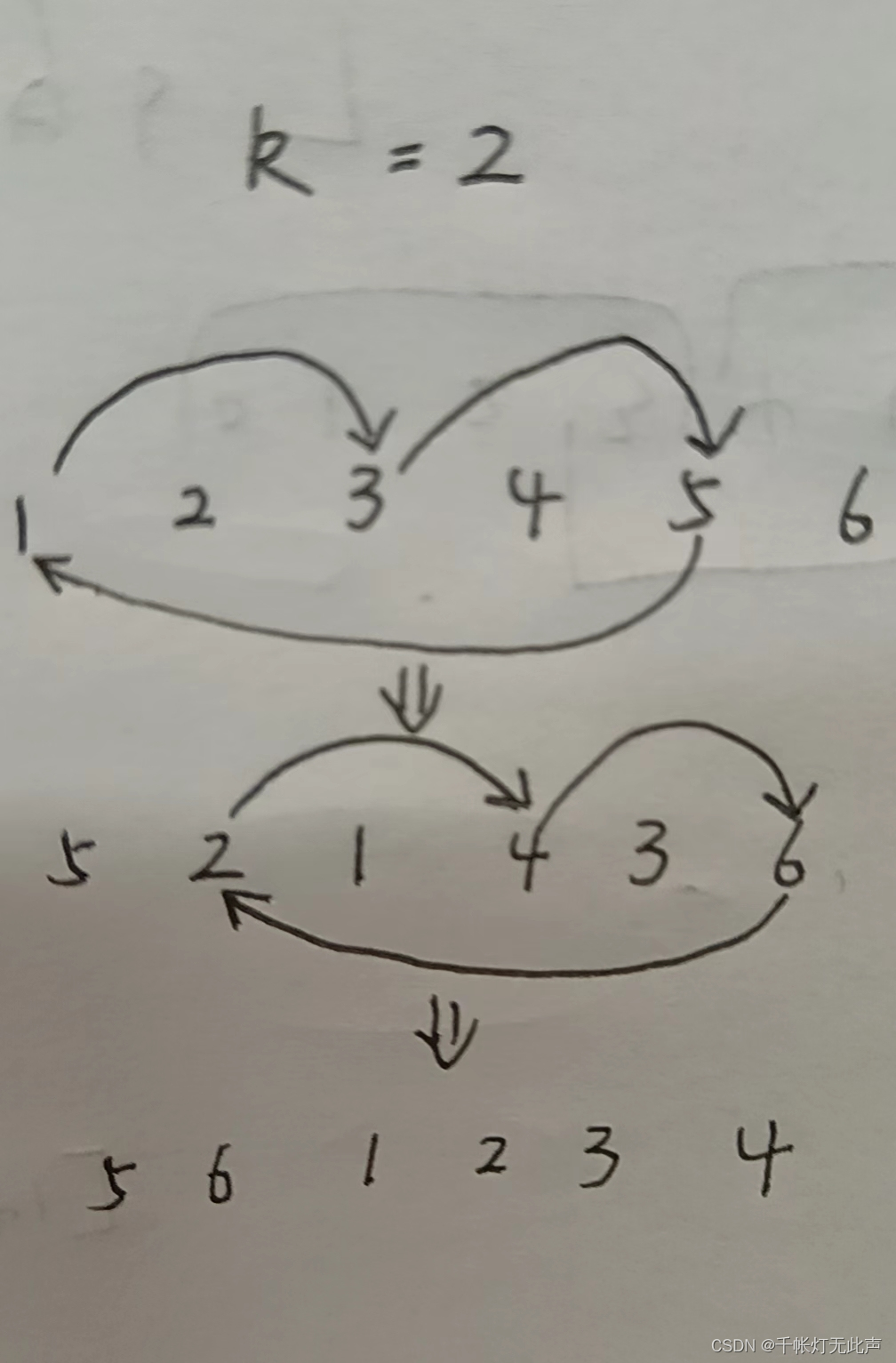
189. 轮转数组 - 力扣(LeetCode)
O(n) 辅助数组
时间复杂度 O(n),空间 O(n)
将末尾的 k 个数,放到开头,会覆盖原来的数,所以需要额外数组
class Solution {
public:void rotate(vector<int>& nums, int k) { // 没有返回值,需要原数组变化int n = nums.size();vector<int> ans(n); // 要指定大小k %= n;int j = 0;for (int i = n - k; i < n; ++i)ans[j++] = nums[i];for (int i = 0; i < n - k; ++i)ans[j++] = nums[i];for (int i = 0; i < n; ++i)nums[i] = ans[i];}
};O(n) 环状替换
空间复杂度优化到 O(1),借助 temp 变量
已知位置 0 的元素会放到 x == (0 + k) % n 的位置,然后 temp = x 依次往后推,直到回到出发位置 0
此时仍有部分元素没有替换到新的位置
需要从 0 的下一位置 1 开始,重复上述步骤
那么一共需要遍历多少次呢,每回到一次出发点,算一次
由题解,需要 gcd(n, k) 次,取 数组长度 和 右移距离 的最大公约数
class Solution {
public:void rotate(vector<int>& nums, int k) {int n = nums.size();k %= n;int count = gcd(n, k);// 遍历的趟数for (int i = 0; i < count; ++i) {// 本趟起点 i,temp 保存被更新的元素int now = i, temp = nums[i];do {int Next = (now + k) % n; // 下一位置// 下一元素被替换,temp 保存被替换元素的值swap(temp, nums[Next]); now = Next;} while (now != i); // 未回到起点}}
};O(n) 数组翻转
思路类似辅助数组的 “将末尾的 k 个数,放到开头”
所以可以先翻转整体,再翻转 [0, k - 1] 和 [k, n - 1]
比如(k = 3) 1 2 3 4 5 6 7 --> 7 6 5 4 3 2 1 --> 5 6 7 1 2 3 4
借助 swap() 创建 reverse() 函数,翻转指定区间的数组
空间优化到 O(1)
class Solution {
public:void reverse(int l, int r, vector<int>& nums) { // 翻转 [l, r] 这个区间for (int i = l, j = r; i < j; ++i, --j)swap(nums[i], nums[j]);}void rotate(vector<int>& nums, int k) {int n = nums.size();k %= n;reverse(0, n - 1, nums);reverse(0, k - 1, nums);reverse(k, n - 1, nums);}
};🌼除自身以外数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode)
O(n) 前缀和
将 前缀和 的思路换成 前缀积,同样,后缀和 变成 后缀积
前缀积数组 l[i] 表示 i 往左所有元素的乘积
后缀积数组 r[i] 表示 i 往右所有元素的乘积
坑
前缀,后缀数组的计算,先模拟一遍
最后不要用 push_back(),会在 n 个 0 的基础上追加 ans[],要用 ans[i] = l[i] * r[i]
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> l(n), r(n), ans(n);l[0] = 1, r[n - 1] = 1; // 0左侧 和 n-1右侧 都没有元素// 预处理 前缀 和 后缀for (int i = 1; i < n; ++i)l[i] = l[i - 1] * nums[i - 1]; // l[2] = l[1] * nums[1]for (int i = n - 2; i >= 0; --i)r[i] = r[i + 1] * nums[i + 1]; // r[2] = r[3] * nums[3]for (int i = 0; i < n; ++i)//ans.push_back(l[i] * r[i]);// 不要用push_back,因为已经初始化了 n 个 0// push_back 会在末尾追加 ans[]ans[i] = l[i] * r[i];return ans;}
};时间O(n) 空间O(1)
在上面前缀和的基础上,只用一个数组 ans[] 代替上面的 3 个数组 l[], r[], ans[]
先用 ans 表示 l[] 数组;在 for 循环中,用变量 r 代替 r[] 数组,同步计算 ans[] 结果
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> ans(n);ans[0] = 1;for (int i = 1; i < n; ++i) // 计算前缀积ans[i] = ans[i - 1] * nums[i - 1];int r = 1; // 代替 r[] 后缀数组for (int i = n - 1; i >= 0; --i) { // 同步计算后缀和ans[]ans[i] *= r; // 前缀 * 后缀r *= nums[i];}return ans;}
};🌙缺失的第一个正数
41. 缺失的第一个正数 - 力扣(LeetCode)
O(n) 哈希
先复习下 map👇
size/empty/clear //元素个数,判空,清空
begin / end //指向开始 / 结束位置的指针
insert(x) //将元素x插入集合(x为二元组)
erase(x) //删除所有等于x的元素(x为二元组)
erase(it) //删除it指向的元素(it为指向二元组的迭代器)
find(k) //查找键为k的二元组的位置, 若不存在, 返回尾指针 .end()复习下 unordered_map👇
std::unordered_map - cppreference.com
std::unordered_map<Key,T,Hash,KeyEqual,Allocator>::insert - cppreference.com
std::unordered_map<Key,T,Hash,KeyEqual,Allocator>::find - cppreference.com
思路
实际就是判断 1~n 是否出现,未出现的就是最小正整数
比较巧妙的思路,用 unordered_map<int, bool> ans 保存出现过的数字,比如,
ans[3] = 1 表示 3 出现过,ans[5] = 0,表示 5 没有出现过
然后 for 遍历 1~n,判断哈希表中这个键是否出现,未出现的就是最小正整数
都出现了,答案就是 n + 1
时空都是 O(n)
哈希表 增删查 (插入删除查找)都是 O(1) 时间复杂度
class Solution {
public:int firstMissingPositive(vector<int>& nums) {int n = nums.size();unordered_map<int, bool> ans;for (auto x : nums)if (x > 0) // 只考虑正整数ans[x] = 1; // 插入键值对// ans.insert(make_pair(x, 1));// ans.insert({x, 1});int num = 0;for (int i = 1; i <= n; ++i) // 判断 1 ~ nif (!ans[i]) { // i 就是最小正整数num = i;break;}if (num == 0) num = n + 1; // 1~n 都出现了return num;}
};O(n) 哈希 + 空间优化(标记)
类似将 vis[] 或 book[] 标记数组,转化为,直接在 a[][] 地图上进行标记的思路
这里我们可以不用哈希表,改为直接在原数组上标记
本质都是判断 1~n 是否在数组里
空间优化为 O(1)
class Solution {
public:int firstMissingPositive(vector<int>& nums) {int n = nums.size();// 处理 0 或 负数,不考虑for (auto& x : nums)if (x <= 0)x = n + 1;for (int i = 0; i < n; ++i) {int num = abs(nums[i]); // 出现过的数会标记为负数if (num <= n) // 1 ~ n 出现了nums[num - 1] = -abs(nums[num-1]); // num 出现,num-1 作为索引标记成负数}for (int i = 0; i < n; ++i)if (nums[i] > 0) // 未标记的为最小正整数return i + 1;return n + 1;}
};O(n) 置换
思路
本质是判断 1~n 是否出现在数组中
那么我们可以将 nums 恢复成 1~n 的形式 [1, 2, 3 ... n]
比如 【3, 4, -1, 1】--> 【1, -1, 3, 4】
int x = nums[i],如果 x ∈ [1, n],那么 nums[i] 原来的位置应该是 nums[x - 1]
比如上面的 3,原来位置应该是下标 2
只需要交换 x 和 i 两个位置的数,此时的 nums[i] 又是新的数,重复上述操作
当 nums[i] == nums[x - 1],说明位置 i 的数据恢复了,就 break 出 while 循环
解释👇
while (nums[i] >= 1 && nums[i] <= n)代码中用 while ,不用 if,因为一次 if 无法把所有代码恢复到初始位置
AC 代码
class Solution {
public:int firstMissingPositive(vector<int>& nums) {int n = nums.size();for (int i = 0; i < n; ++i) {while (nums[i] >= 1 && nums[i] <= n) {int x = nums[i];swap(nums[x - 1], nums[i]); // nums[i] 放到原来的位置 x-1if (nums[x - 1] == nums[i]) break; // 位置已恢复(防止死循环)}}for (int i = 0; i < n; ++i)if (nums[i] != i + 1)return i + 1;return n + 1;}
};

)




)








(附效果图及在线演示))

)


