目录
100231. 超过阈值的最少操作数 I
原题链接
思路分析
AC代码
100232. 超过阈值的最少操作数 II
原题链接
思路分析
AC代码
100226. 在带权树网络中统计可连接服务器对数目
原题链接
思路分析
AC代码
100210. 最大节点价值之和
原题链接
思路分析
AC代码
100231. 超过阈值的最少操作数 I
原题链接
超过阈值的最少操作数 I - 力扣 (LeetCode) 竞赛
思路分析
签到题,没啥说的
AC代码
class Solution {
public:int minOperations(vector<int>& nums, int k) {sort(nums.begin(), nums.end());return lower_bound(nums.begin(), nums.end(), k) - nums.begin();}
};100232. 超过阈值的最少操作数 II
原题链接
100232. 超过阈值的最少操作数 II
思路分析
数组放到小根堆,检测是否全部大于等于k
如果有小于k的,就弹出俩元素,添加新元素
AC代码
class Solution
{
public:int minOperations(vector<int> &nums, int k){long long res = 0, a, b;priority_queue<long long, vector<long long>, greater<long long>> pq;for (auto x : nums)pq.emplace(x);while (pq.top() < k)a = pq.top(), pq.pop(), b = pq.top(), pq.pop(), pq.emplace(a * 2 + b), res++;return res;}
};100226. 在带权树网络中统计可连接服务器对数目
原题链接
100226. 在带权树网络中统计可连接服务器对数目
思路分析
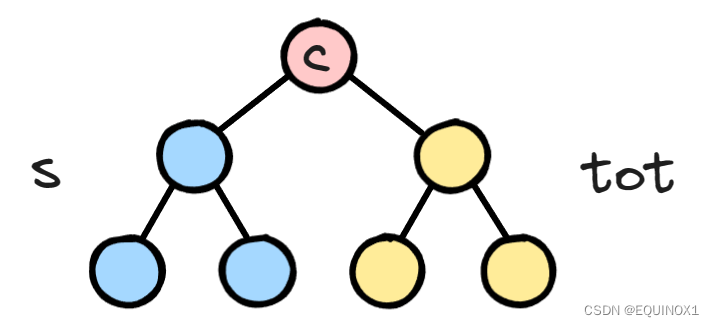
枚举中间服务器c,顺序从邻接点往下遍历,假如对某个邻接点遍历,得到可被整除路径数目为tot,之前遍历到的可被整除路径数目为s,那么根据乘法原理,答案要增加tot*s
计算中间服务器c的贡献需要O(N),n个点计算一遍是O(N^2)
AC代码
const int N = 1005, M = N * N;
class Solution
{
public:struct edge{int v, w, nxt;} edges[M];int head[N], idx = 0;void addedge(int u, int v, int w){edges[idx] = {v, w, head[u]}, head[u] = idx++;}vector<int> countPairsOfConnectableServers(vector<vector<int>> &g, int signalSpeed){int n = g.size() + 1, tot = 0;memset(head, -1, sizeof head), idx = 0;vector<int> ret(n);for (auto &e : g)addedge(e[0], e[1], e[2]), addedge(e[1], e[0], e[2]);function<void(int, int, int)> dfs = [&](int u, int fa, long long pre){if ((pre % signalSpeed) == 0)tot++;for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (v == fa)continue;dfs(v, u, pre + edges[i].w);}};for (int u = 0, s = 0; u < n; u++){s=0;for (int i = head[u], v; ~i; i = edges[i].nxt){tot = 0, v = edges[i].v, dfs(v, u, edges[i].w);ret[u] += s * tot, s += tot;}}return ret;}
};100210. 最大节点价值之和
原题链接
最大节点价值之和 - 力扣 (LeetCode) 竞赛
思路分析
我们考虑,最终得到的最大数组和原数组相比看,可不可能只有奇数个元素发生变化
答案是不可能,自己可以模拟一下
因此必然有偶数个数发生变化
而对于numi和numj如果发生变化,我们一定可以做到只改变numi和numj而不影响其它元素
只要把路径上的边都操作一遍即可
所以问题就变成了偶数个数目进行异或k后数组的最大和
这个线性dp即可,跟树没关系
AC代码
class Solution {
public:long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {long long f0 = 0, f1 = -1e9, t;for(int x : nums) t = f0, f0 = max(f0 + x, f1 + (x ^ k)), f1 = max(t + (x ^ k), f1 + x);return f0;}
};

)



)

)
)





)



