1005. K 次取反后最大化的数组和

简单

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组 可能的最大和 。

class Solution {public int largestSumAfterKNegations(int[] nums, int k) {// 先按绝对值大到小排个序reverseAbsNms(nums);for (int i = 0; i < nums.length; i++) {//从前往后遍历，遇到负数将其变为正数，同时K--if (nums[i] < 0 && k > 0) { // K > 0也是个很重要的条件nums[i] = -nums[i];k--;}}// 如果K还大于0，那么反复转变数值最小的元素，将K用完if (k % 2 == 1) nums[nums.length - 1] = -nums[nums.length - 1];int sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];}return sum;}public void reverseAbsNms(int[] nums) {for (int i = 0; i < nums.length - 1; i++) {for (int j = 0; j < nums.length - i - 1; j++) {if (Math.abs(nums[j]) < Math.abs(nums[j + 1])) { // 是j不是i ！！！int temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp; }}}}
}

134. 加油站

中等
在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

难点：总油量减去总消耗大于等于零为什么一定可以跑完一圈？i如果无法到j的话，那么i和j之间的点也无法到达j的理论，推不出来就背吧

class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {int n = gas.length;// 考虑从每一个点出发 for (int start = 0; start < n; ) {if (gas[start] < cost[start]) {start++; // 这个点连到下一个点都做不到，换个点继续试} else {int remain = gas[start] - cost[start];int idx = start + 1;while (idx % n != start) {remain += gas[idx % n] - cost[idx % n];if (remain < 0) {break;}idx++; }if (idx % n == start) {return start;} else {start = idx; // 就是那个i如果无法到j的话，那么i和j之间的点也无法到达j的理论，推不出来就背吧}}}// 任何点都不可以return -1;}
}

135. 分发糖果

困难
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

/*
分两个阶段
1、起点下标1 从左往右，只要 右边 比 左边 大，右边的糖果=左边 + 1
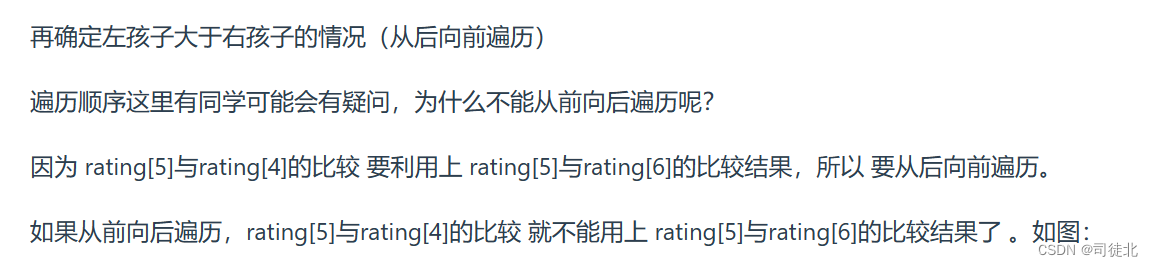
2、起点下标 ratings.length - 2 从右往左， 只要左边比右边大，此时 
左边的糖果应该 取本身的糖果数（符合比它左边大） 和 右边糖果数 + 1 二者的最大值，
这样才符合 它比它左边的大，也比它右边大*/
class Solution {public int candy(int[] ratings) {int[] candyNums = new int[ratings.length];Arrays.fill(candyNums, 1);// 从前向后for (int i = 1; i < ratings.length; i++) {// 右比左大if (ratings[i] > ratings[i - 1]) candyNums[i] = candyNums[i - 1] + 1;}// 从后向前 int result = candyNums[ratings.length - 1];for (int i = ratings.length - 2; i >= 0; i--) {// 左比右大if (ratings[i] > ratings[i + 1]) {// 取本身的糖果数（符合比它左边大） 和 右边糖果数 + 1 二者的最大值，//这样才符合 它比它左边的大，也比它右边大candyNums[i] = Math.max(candyNums[i], candyNums[i + 1] + 1);}result += candyNums[i];}return result;}
}