●139.单词拆分 

物品：wordDict里面的单词；背包容量：s.size()。

1.dp[j]含义。dp[j]=true表示字符串前j个可以拆分成字典中的单词。dp[s.size()] 就是最后的结果，整个字符串能（true）不能（false）拆分成字典中的单词。

2.递推公式。如leetcode，依次从l、le、lee、……、leetcode这8个字符串来检查是否能拆分成字典中的单词，最后返回 dp[s.size()] 这是外循环。然后对于每个字符串strj的检查，如果这个单词中有某个位置k为true（代表0到k这个位置可以拆分）且从k+1到这个单词的结束位置j的子串（strj字符串剩下的子串）在wordDict里面，就说明这个字符串strj从0到j都能拆分，所以dp[j]更新为true，检查这个位置k就得从字符串strj的开始到结尾了，取不取j都可以，这就是内循环。

所以这样理解的话也确定了循环顺序，外循环是背包（j从1到s.size()），内循环也是也是背包（i从0到 j-1），就跟以前做的题不太一样。

3.初始化。dp[0]应该初始化为true，否则逐个判断后面的元素不会得到true的值，其他的一开始就应该是false，然后后面再挨个更新，看是否换成false。

4.遍历顺序。根据之前的推理两层循环都是背包，物品集合只是在循环里面做条件使用的。

5.打印。

代码如下。

j=0初始为true，其他的初始为false，

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {//物品：wordDict。//背包容量：svector<bool> dp(s.size()+1,false);  dp[0]=true;unordered_set<string> wordSet(wordDict.begin(),wordDict.end());for(int j=1;j<=s.size();++j){for(int i=0;i<j;++i){string sub=s.substr(i,j-i);if(wordSet.find(sub)!=wordSet.end() && dp[i]){dp[j]=true;}}}return dp[s.size()];}
};

● 关于多重背包，你该了解这些！ 

多重背包问题：有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量，且价值总和最大。

每件物品的最多Mi件可用，其实可以把Mi展开，就变成了01背包问题。

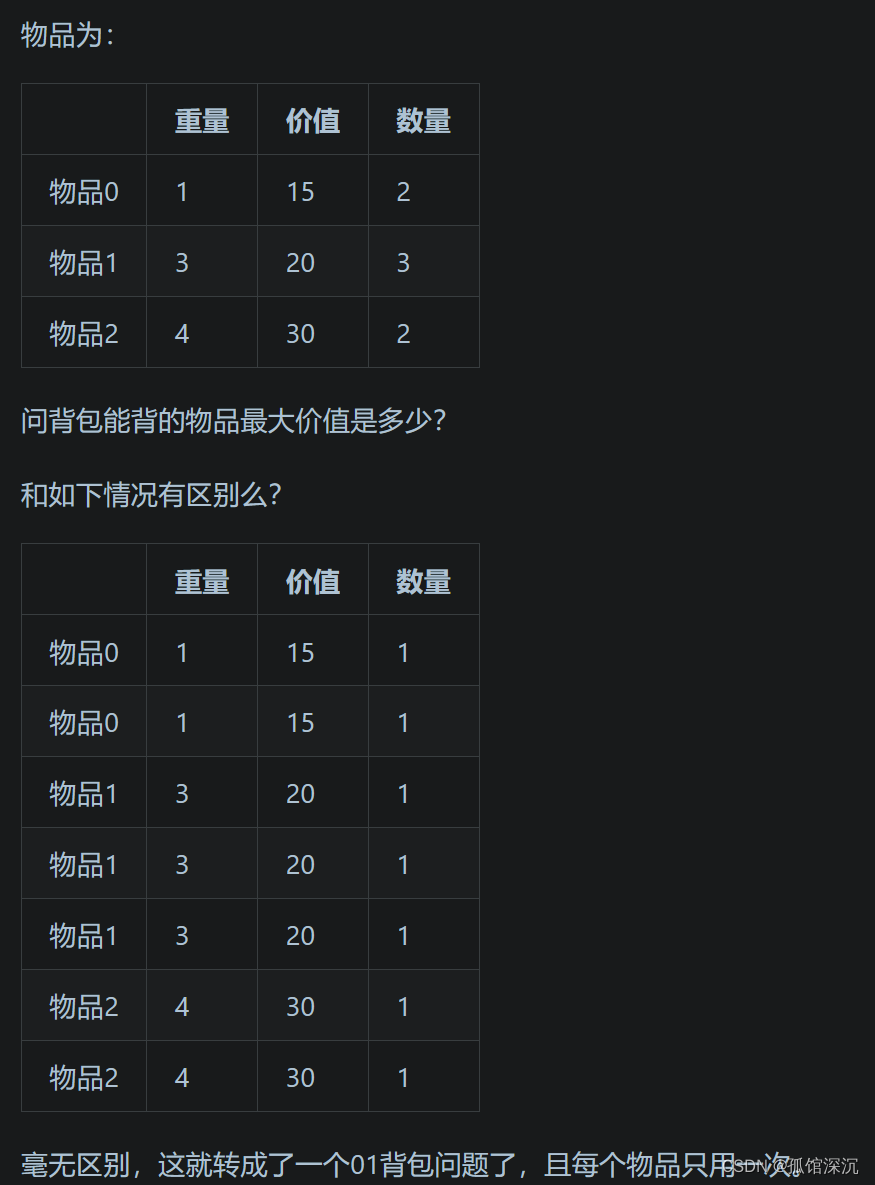
所以最直接的方法就是在重量数组和价值数组里面都把这些展开了的加入进去，物品0增加为2个……但是会超时。主要消耗在vector的动态底层扩容上。

 for (int i = 0; i < n; i++) {while (nums[i] > 1) { // 物品数量不是一的，都展开weight.push_back(weight[i]);value.push_back(value[i]);nums[i]--;}}

还有方法就是不改变这两个数组，我们知道纯01背包问题可以先物品，也可以先背包，然后考虑物品i放不放入两种情况，01背包放入就只会放入一个，所以就一个递推语句；但是多重背包可以放1个、……nums[i]个，所以每个物品i得有nums[i]个递推。so解决纯多重背包问题，要从纯01背包问题的递推代码：

dp[j]=max(dp[j-weight[i]]+value[i],dp[j]]

改为：

for(int k=1;k<=nums[i];++k){if(j>=k*weight[i]){dp[j]=max(dp[j-k*weight[i]]+k*value[i],dp[j]);}
}

即每个物品，都考虑不放和放k个多种情况。

代码如下：

#include<vector>
#include<iostream>
using namespace std;
void maxValue(){int begweight,N;cin >> begweight >> N;vector<int> dp(begweight+1,0);vector<int> nums(begweight+1);vector<int> weight(N);vector<int> value(N);for (int i = 0; i < N; i++) cin >> weight[i];for (int i = 0; i < N; i++) cin >> value[i];for (int i = 0; i < N; i++) cin >> nums[i];for(int i=0;i<N;++i){//先物品for(int j=begweight;j>=weight[i];--j){for(int k=1;k<=nums[i];++k){if(j>=k*weight[i])dp[j]=max(dp[j-k*weight[i]]+k*value[i],dp[j]);}}}cout<<dp[begweight];
}int main(){maxValue();return 0;
}

注意，在随想录中说：多重背包在面试中基本不会出现，力扣上也没有对应的题目，大家对多重背包的掌握程度知道它是一种01背包，并能在01背包的基础上写出对应代码就可以了。

●背包问题总结篇！