Em...属于一知道就会,不知道的话比较难想。
我们先看题:

我们不妨把1抽象成一个平面上的点,因此可以变成这一幅图:

我们假设每一个点被向上牵拉了一根线:
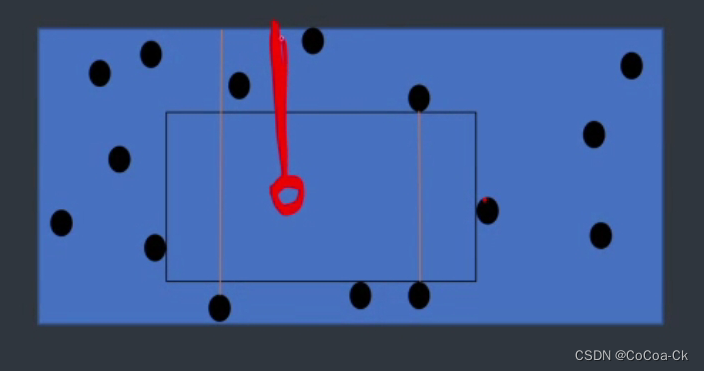
显然,每一条悬线都有可能成为边界限制,我们确定一条悬线,乘上悬线最左可到的+最右可到的距离即可。
首先,对于上下边界的悬线,我们记h[i][j]为(i,j)的悬线长度,易得方程:
h[i][j]=h[i-1][j]+1(a[i][j]=0)或者=0(a[i][j]=1).
我们再维护向左的长度。
我们记l[i][j]表示向左最远.l[i][j]=l[i][j-1]+1(a[i][j]=0)/0(a[i][j]=1)
我们记L[i][j]表示(i,j)这条悬线向左最远。
L[i][j]=min(L[i-1][j],l[i][j]).
向右同理。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int l[100][100],r[100][100],h[100][100],n,a[90][90];
int main(){cin>>n;int ans=0;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(a[i][j]==1){h[i][j]=0;l[i][j]=0;}else{h[i][j]=h[i-1][j]+1;l[i][j]=l[i][j-1]+1;}}for(int j=n;j>=1;j--){if(a[i][j]==1){r[i][j]=0;}else r[i][j]=r[i][j+1]+1;}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(h[i][j]>=2){//注意为2,若为1时会把上面的0带下来,而事实上1的值不用改l[i][j]=min(l[i][j],l[i-1][j]);r[i][j]=min(r[i][j],r[i-1][j]);}ans=max(ans,(r[i][j]+l[i][j]-1)*h[i][j]);}}cout<<ans;
} 那么如果要求是正方形呢?
很简单,我们只要把h[i][j]与r[i][j]+l[i][j]-1取min并平方即可。
我们来看一个变形题吧:

这里有两种方法:
1.我们还是用悬线,只不过转移条件需要修改(与自己颜色不同时转移)
2.我们先进行染色操作,我们按照国际象棋去染色,我们把国际象棋为1的位置进行颠倒。1变成0,0变成1,我们再求其中的全0/1最大子矩形即可(我们反着看,把全0/1的恢复一下不就是了吗)
下面给出法2的AC代码:
#include<bits/stdc++.h>
using namespace std;
int l[2010][2010],r[2010][2010],h[2100][2010],n,m,a[2010][2010];
int l1[2010][2010],r1[2010][2010],h1[2100][2010];
int main(){cin>>n>>m;int ans0=0,ans1=0,ans00=0,ans11=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);}}int cnt=1;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(j%2==cnt) a[i][j]=1-a[i][j];}cnt=1-cnt;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]==1){h[i][j]=0;l[i][j]=0;}else{h[i][j]=h[i-1][j]+1;l[i][j]=l[i][j-1]+1;}}for(int j=m;j>=1;j--){if(a[i][j]==1){r[i][j]=0;}else r[i][j]=r[i][j+1]+1;}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(h[i][j]>=2){l[i][j]=min(l[i][j],l[i-1][j]);r[i][j]=min(r[i][j],r[i-1][j]);}ans0=max(ans0,(r[i][j]+l[i][j]-1)*h[i][j]);ans00=max(ans00,min(r[i][j]+l[i][j]-1,h[i][j])*min(r[i][j]+l[i][j]-1,h[i][j]));}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]==0){h1[i][j]=0;l1[i][j]=0;}else{h1[i][j]=h1[i-1][j]+1;l1[i][j]=l1[i][j-1]+1;}}for(int j=m;j>=1;j--){if(a[i][j]==0){r1[i][j]=0;}else r1[i][j]=r1[i][j+1]+1;}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(h1[i][j]>=2){l1[i][j]=min(l1[i][j],l1[i-1][j]);r1[i][j]=min(r1[i][j],r1[i-1][j]);}ans1=max(ans1,(r1[i][j]+l1[i][j]-1)*h1[i][j]);ans11=max(ans11,min(r1[i][j]+l1[i][j]-1,h1[i][j])*min(r1[i][j]+l1[i][j]-1,h1[i][j]));}}cout<<max(ans00,ans11)<<endl;cout<<max(ans0,ans1);
} 

![Bulingbuling - 《历史的教训》 [ The Lessons of History ]](http://pic.xiahunao.cn/Bulingbuling - 《历史的教训》 [ The Lessons of History ])

)




0.5.000)






)


